НОУ ИНТУИТ | Проектирование систем искусственного интеллекта. Лекция 10: Машинная эволюция

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 15.06.2007 | Доступ: свободный | Студентов: 6625 / 2725 | Оценка: 3.96 / 3.52 | Длительность: 15:17:00

Тема: Искусственный интеллект и робототехника

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Автоматический синтез технических решений

Каждый настоящий изобретатель, каждый творчески работающий конструктор не просто ищет новое, улучшенное ТР, а стремится найти самое эффективное, самое рациональное, лучшее из лучших решений. И такие решения некоторым изобретателям удавалось находить. Это, например, конструкция книги, карандаша, гвоздя, брюк, велосипеда, трансформатора переменного тока, паровой машины и многих других ТО. Такие конструкции в первую очередь характеризуются тем, что они сотни или десятки лет массово производятся и используются без изменения, если не считать мелких усовершенствований.

Наивысшее достижение инженерного творчества заключаются в нахождении глобально оптимальных принципов действия и структур ТО.

Поиск оптимальных структур

Постановка задачи параметрической оптимизации. Прежде чем рассматривать постановку задачи поиска оптимального ТР для заданного физического принципа действия, разберем задачу более низкого уровня, которую называют задачей поиска оптимальных значений параметров для заданного ТР или сокращенно — задачей параметрической оптимизации. Эти задачи неизбежно приходится решать при поиске оптимального ТР, а кроме того, они имеют и самостоятельное значение.

Любое отдельное ТР, как правило, можно описать единым набором переменных (изменяемых параметров)

Х = (x₁, ..., x_n), (1)

которые могут изменять свои значения в некотором гиперпараллелепипеде

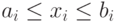$a_i\le x_i\le b_i$ , i = l, ..., n, (2)

где для расширения области поиска не рекомендуется накладывать жестких ограничений на a_i, b_i.

Математическая модель проектируемого изделия ставит в соответствие каждому набору значений (1) некоторый критерий качества (функцию цели) f(х) и накладывает на переменные (1) дополнительные ограничения, представляемые чаще всего в виде системы нелинейных неравенств

$g_i (X) \ge 0, j = 1,...,m$

( 3)

,

Тогда задача поиска оптимальных параметров ТР состоит в нахождении такого набора (1), который удовлетворяет неравенствам (2) и (3) и обеспечивает глобальный экстремум критерию качества. Для определенности будем считать, что отыскивается минимум, и, если обозначим через D область допустимых решений, удовлетворяющих неравенствам (2), (3), получим задачу математического программирования в n -мерном пространстве:

найти точку $X* \in D$ , такую, что

$F(X^*)=\min\limits_{X\in D}F(X)$

( 4)

Часто в задачах параметрической оптимизации на переменные или часть из них наложены условия целочисленности или дискретности. В этом случае область поиска D становится заведомо многосвязной, а сама задача с математической точки зрения — многоэкстремальной.

Следует еще заметить, что задачи поиска оптимальных значений параметров в подавляющем большинстве случаев представляют собой многопараметрические многоэкстремальные задачи, в которых функциональные ограничения (3) "вырезают" замысловатые допустимые области. Объемы этих областей могут быть очень малыми по сравнению с объемами гиперпараллелепипедов (2). Однако, несмотря на такую сложность, большинство задач параметрической оптимизации можно вполне удовлетворительно решить существующими методами.

Постановка задачи структурной оптимизации. Среди задач поиска оптимальных ТР рассмотрим только подкласс, называемый задачами поиска оптимальных многоэлементных структур ТО, или коротко — задач структурной оптимизации.

Строгое определение понятия структуры ТО дать затруднительно, поэтому укажем лишь некоторые инженерные и математические свойства, которые связаны с этим понятием.

С инженерной точки зрения, разные структуры рассматриваемого класса ТО отличаются числом элементов, самими элементами, их компоновкой, характером соединения между элементами и т. д. Понятие структуры в большой мере аналогично понятию технического решения, данному в п. 3 "Базовые понятия" , однако имеются различия, которые вызывают необходимость введения этого дополнительного понятия. Во-первых, в рамках заданного физического принципа действия, как правило, существует более широкое множество ТР по сравнению с множеством, которое можно формально описать при постановке и решений задачи структурной оптимизации. Во-вторых, между отдельными ТР подразумеваются более существенные различия по конструктивным признакам, чем различия между отдельными структурами, иногда формально отличающимися значениями несущественных дискретных переменных. Например, на рис. 10.1 показаны две фермы моста с решеткой в виде равнобедренных треугольников, которые имеют одинаковые ТР, но разные структуры. Короче говоря, для заданного физического принципа действия множества возможных ТР и множество возможных структур (для рассматриваемой задачи структурной оптимизации) пересекаются, но, как правило, не совпадают.

При этом одно ТР можно представить несколькими близкими структурами.

С математической точки зрения два варианта ТО будут иметь различную структуру, если соответствующие им задачи параметрической оптимизации по одному и тому же критерию качества и при условии выбора оптимальных параметров каждого элемента структуры имеют различные наборы переменных (1) и функции (3), т. е. для различных структур существуют различные задачи параметрической оптимизации. Под критерием качества также подразумевается физико-технический, экономический или другой показатель (масса, точность, мощность, стоимость и т. п.), по значению которого из любых двух структур можно выбрать лучшую.

Рис. 10.1. Пример различных структур при одинаковом ТР

Постановку задач структурной оптимизации обычно начинают с определения набора переменных по следующей методике.

Задают такие переменные, чтобы они могли по возможности описать множество всех рациональных структур S₀, которые в состоянии оценить существующая математическая модель в рассматриваемом классе ТО.
Просматривают и анализируют методы преобразования структур. Дополняют множество S₀ подмножествами новых структур, которые можно синтезировать и оценить с помощью существующей или доработанной математической модели. В результате строится расширенное множество рассматриваемых структур S и описывающий его набор переменных, который обозначим вектором А. Пусть, например, задача структурной оптимизации допускает следующий набор А:

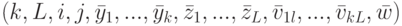
$(k,L,i,j, \bar y_1, ... , \bar y_k, \bar z_1, ... , \bar z_{L}, \bar v_{1l}, ... , \bar v_{kL} , \bar w)$ ( 5)

где k — число элементов в структуре;

L — число способов соединения элементов;

$\bar y_i$ — вектор, описывающий геометрические, физические и другие свойства i -го элемента;

i — номер элемента (1, ..., k),

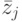$\bar z_j$ — вектор, описывающий геометрические, физич еские и другие свойства j -го способа соединения:

j — номер способа соединения (1,...,L) ;

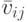$\bar v_{ij}$ — вектор, характеризующий положение i-го элемента в пространстве при j -м способе соединения (i = 1, ..., k, j = l, ..., L) ;

$\bar w$ — другие переменные.
Из вектора А выделяют вектор А' независимых переменных, которыми можно варьировать при поиске оптимальных структур. Для зависимых переменных задают алгоритм их определения через независимые переменные.
Вектор А' разделяют на вектор переменных A'_S, обеспечивающих изменение структуры, и вектор переменных А'_P, с помощью которых ставят и решают задачи параметрической оптимизации для заданной структуры. Вектор А'_P состоит из набора общих переменных А'₀, которые присутствуют при изменении любой структуры, и набора переменных А'_C, изменяющихся при переходе от структуры к структуре. При решении задачи параметрической оптимизации для заданной структуры используется только определенная часть переменных из набора А_с.

Так, если в задаче структурной оптимизации с указанным набором переменных структура определяется способом соединения, то можно считать, что A'_S есть одна переменная

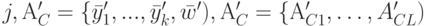
$j, А'_C = \{\bar y'_1 , ...,\bar y'_k , \bar w' ), А'_C = \{А'_{C1}, …, A'_{CL})$

где 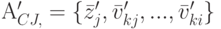$А'_{CJ,} = \{\bar z'_j ,\bar v'_{kj} ,..., \bar v'_{ki} \}$ — собственные переменные j -й структуры; штрих означает, что среди соответствующих переменных выбраны независимые.

Допустим, имеется алгоритм выбора из множества S подмножества всех допустимых структур {S_i,..., S_m}, у которых существует хотя бы один набор значений параметров, удовлетворяющих заданным ограничениям. Допустим также, что для любой структуры S_J (j = 1, ..., m) можно решить задачу параметрической оптимизации, т. е. задать пространство переменных

$\overline{X}_j=(x_1^j,K,x_{nj}^j)$ , j = 1, …, m,(6)

и по единому критерию качества найти допустимые оптимальные параметры структуры S_J. Оптимальные значения параметров структуры S_J будем обозначать через 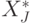X^*_J .

Тогда задаче структурной оптимизации можно дать следующую формулировку.

Имеется m n_J -мерных параллелепипедов

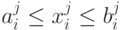$a_i^j \le x_i^j \le b_i^j$ , i = 1, …, n_J, j = 1, …, m,(7)

как с непрерывным, так и с дискретным характером изменения переменных . Для каждого из параллелепипедов задана по единому критерию качества целевая функция

$f=f'(\overline{X}_j)$ , j = 1, …, m,(8)

и система ограничений

$g'_r(\overline{X}_j) \ge 0$ , r = 1, …, p_J, j = 1, …, m, (9)

Требуется найти точку 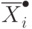$\overline{X}^{\bullet}_i$ , принадлежащую 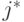j^* -му параллелепипеду, для которой

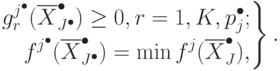
$\left{ \begin{aligned} g_r^{j^{\bullet}}(\overline{X}^{\bullet}_{J^{\bullet}})\ge 0, r=1,K,p_j^{\bullet};\\ f^{j^{\bullet}}(\overline{X}^{\bullet}_{J^{\bullet}})= \min f^j(\overline{X}^{\bullet}_{J}), \end{aligned} \right\}.$

Таким образом, задача структурной оптимизации состоит в нахождении глобально-оптимальной структуры и глобально-оптимальных значений переменных внутри этой структуры, т. е. эту задачу можно назвать также задачей структурно-параметрической оптимизации.

К задачам структурной оптимизации относится задача выбора оптимальной компоновки ТО.

Отметим некоторые особенности задач структурной оптимизации. Во-первых, почти всегда в этих задачах одновременно присутствуют и дискретные, и непрерывные переменные, т. е. задачи структурной оптимизации в общем случае относятся к смешанным задачам математического программирования. Во-вторых, при структурных преобразованиях изменяются число и характер переменных и соответственно функции ограничений и целевые функции. Что касается характера многосвязной области поиска, то отдельные подобласти или имеют различную размерность, или (при совпадении размерности) образованы различными наборами переменных.

Дальше >>

Авторизоваться

Проектирование систем искусственного интеллекта

Машинная эволюция

Автоматический синтез технических решений

Поиск оптимальных структур

Вопросы и ответы