НОУ ИНТУИТ | Проектирование систем искусственного интеллекта. Лекция 10: Машинная эволюция

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 15.06.2007 | Доступ: свободный | Студентов: 6625 / 2725 | Оценка: 3.96 / 3.52 | Длительность: 15:17:00

Тема: Искусственный интеллект и робототехника

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Алгоритм поиска глобального экстремума

Алгоритм поиска глобально-оптимального решения можно использовать для решения задач как параметрической, так и структурной оптимизации. Укрупненная блок-схема алгоритма включает четыре процедуры:

синтез допустимой структуры (СДС), обеспечивающий выбор допустимого решения из любой подобласти всей области поиска;
шаг локального поиска (ШЛП), обеспечивающий переход от одного решения к другому допустимому решению, как правило, той же структуры, но с улучшенным значением критерия; под шагом локального поиска можно понимать некоторый условный шаг по какому-либо алгоритму поиска локального экстремума (например, одна итерация по методу наискорейшего спуска);
глобальный поиск, управляющий работой процедур СДС и ШЛП;
проверка условий прекращения поиска, определяющая конец решения задачи.

Приведем основные рекомендации построения процедур СДС и ШЛП.

В некоторых случаях построение процедуры СДС можно свести к предварительному составлению набора допустимых структур, из которого выбирают структуры при каждом обращении к процедуре СДС. Если суть этой процедуры состоит в выборе по возможности допустимого набора переменных структурной оптимизации, то представляется полезным включать в нее правила выбора переменных, основанные на эвристических соображениях, аналитических и экспериментальных исследованиях, изучении опыта проектирования и эксплуатации аналогичных TО. Для некоторых сложных или малоизученных задач проектирования трудно построить процедуру СДС, обеспечивающую получение допустимых структур. В этом случае в процедуру целесообразно включать операции преобразования недопустимых структур в допустимые. Набор таких операций можно составить из подходящих эвристических приемов (для задач, связанных с техническими объектами, сборники таких приемов можно найти в соответствующей литературе, в которой решение изобретательских задач рассматривается более подробно). Преобразование недопустимых структур в допустимые можно также решать как задачу оптимизации. В диалоговом режиме работы санкцию процедуры СДС может взять на себя проектировщик.

В целом по процедуре СДС можно дать следующие рекомендации, направленные на повышение вероятности выбора допустимых структур и снижение объема вычислений по оценке недопустимых:

способы выбора значений переменных должны содержать правила, отсекающие заведомо нерациональные и недопустимые значения переменных и их комбинации;
ограничения следует проверять не после построения структуры в целом, а по возможности в процессе построения, что позволяет сократить лишнюю работу по ненужным построениям и в ряде случаев сразу внести поправки по устранению дефектов структуры;
проверяемые ограничения должны быть упорядочены по снижению вероятности их нарушения; такое упорядочение иногда можно проводить автоматически в процессе решения задачи.

Процедуры ШЛП включают обычно способы изменения переменных, ориентированные на решение задач как структурной, так и параметрической оптимизации. Приведенные рекомендации по построению процедур СДС можно использовать и при построении способов локального изменения дискретных переменных. Для изменения непрерывных переменных, как правило, применяют различные алгоритмы локального поиска. Ниже указаны наиболее предпочтительные (о ГА смотри замечание ниже).

В качестве процедуры глобального поиска применяется алгоритм конкурирующих точек. В основе этого алгоритма лежит принцип эволюции популяции живых организмов, находящихся в ограниченном пространстве, например, на острове. В такой популяции резко обостряется конкуренция между отдельными особями. В связи с этим в основу алгоритма конкурирующих точек положены следующие положения:

поиск глобального экстремума осуществляется несколькими конкурирующими решениями (точками);
условия конкуренции одинаковых для всех решений;
в определенные моменты некоторые "худшие" решения бракуются (уничтожаются);
последовательный локальный спуск каждого решения (вначале грубый, затем более точный) происходит независимо от спуска других решений.

Конкуренция позволяет за счет отсева решений, спускающихся в локальные экстремумы, достаточно быстро находить глобальный экстремум в задачах, для которых значение функционала, осредненное по области притяжения глобального экстремума, меньше значения функционала, осредненного по всей области поиска, а область притяжения глобального экстремума не слишком мала.

Алгоритм конкурирующих точек — один из наиболее простых и эффективных по сравнению с другими распространенными алгоритмами поиска глобального экстремума. Так, например, трудоемкость поиска (затраты машинного времени) по этому алгоритму на порядок меньше по сравнению с алгоритмом случайного перебора локальных экстремумов и на два порядка меньше по сравнению с методом Монте-Карло.

Для удобства изложения алгоритма решение будем называть также точкой (в многомерном пространстве поиска) и независимо от того, решается ли задача параметрической оптимизации (1)—(4) или задача структурной оптимизации (6)—(9), будем обозначать его X.

Алгоритм конкурирующих точек

Алгоритм конкурирующих точек в общем виде включает следующие операции.

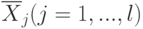По процедуре СДС синтезируется $l(l=\eta + \lambda_0)$ точек $\overline{X}_j (j=1,...,l)$ , в которых определяется значение минимизируемой функции (критерия сравнения). Из этих точек отбирается $\eta$ точек, имеющих наилучшие значения критерия, которые в дальнейшем называются основными. Запоминается наихудшее значение критерия основных точек $\phi_0$ . При этом считается, что совершен нулевой глобальный (групповой) шаг поиска (t = 0).

Таким образом, на t -м групповом шаге поиска имеем основные точки

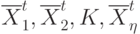
$\overline{X}_1^t,\overline{X}_2^t,K,\overline{X}_{\eta}^t$ ( 10)

и, соответственно, невозрастающую последовательность чисел

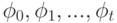
$\phi_0,\phi_1,...,\phi_t$ ( 11)
Каждая основная точка делает шаг локального поиска, в результате чего точки (10) переходят в новую последовательность

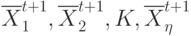
$\overline{X}_1^{t+1},\overline{X}_2^{t+1},K,\overline{X}_{\eta}^{t+1}$ ( 12)
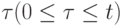Синтезируется $\lambda_{t+1}$ дополнительных допустимых точек, каждой из которых разрешается сделать t+1 шагов локального поиска при условии, что после каждого шага с номером $\tau (0 \le \tau \le t)$ ее критерий не хуже, чем соответствующий член последовательности (11). При нарушении этого условия точка исключается и не участвует в дальнейшем поиске глобального экстремума. Таким образом, имеется $q(q\le \lambda_{t+1})$ дополнительных точек, сделавших t+1 шаг локального поиска:

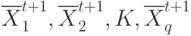
$\overline{X}_1^{t+1},\overline{X}_2^{t+1},K,\overline{X}_{q}^{t+1}$ ( 13)
Среди точек (12) и (13) отбирается $\eta$ точек с лучшими критериями:

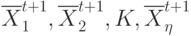
$\overline{X}_1^{t+1},\overline{X}_2^{t+1},K,\overline{X}_{\eta}^{t+1}$ ( 14)

которые являются основными на t+1 -м групповом шаге поиска. Значение худшего критерия точек из последовательности (14) дополняет последовательность (11) числом $\phi_{t+1}$ .
Цикл по пп. 2—4 повторяется до нахождения глобального экстремума по заданным условиям прекращения поиска. В качестве условий прекращения поиска могут быть использованы, например, выполнение заданного числа Т групповых шагов.

Считая параметры 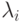$\lambda_i$ независимыми от i, будем иметь только два настраиваемых параметра алгоритма; $\eta$ — число основных точек и $\lambda$ — число дополнительных точек.

Проведенные исследования позволяют рекомендовать следующие оптимальные значения этих параметров: 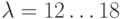$\eta = 2…3$ , $\lambda = 12…18$ . Для простоты реализации алгоритма можно брать постоянные значения $\eta$ и $\lambda$ .

В качестве процедуры ШЛП рекомендуется использовать следующие алгоритмы поиска локального экстремума:

алгоритм случайного поиска в подпространствах;
алгоритм случайного поиска с выбором по наилучшей пробе;
алгоритм сопряженных градиентов;
алгоритм Нельдера-Мида.

Алгоритм случайного поиска в подпространствах

Рекомендуемый алгоритм случайного поиска в подпространствах можно записать в виде следующих рекуррентных выражений:

$\overline{X}_{i+1}=\overline{X}_{i}+\Delta \overline{X}_{i+1}$ ;

$\overline{X}_{i}=\overline{X}_{i-h}$ при $[ f(\overline{X}_{i-1})<f(\overline{X}_{i}) ] \vee [g(\overline{X}_{i})<0]$ .

Здесь h — число последовательно неудачных шагов поиска; $\Delta \overline{X}_{i+1}$ определяется по формуле:

$\Delta \overline{X}_{i+1}= \begin{cases} a \overline{\zeta}_{i+1} \text{ при } (i=0)\vee(|\Delta \overline{X}_{i}|=|\Delta \overline{X}_{i-1} |)\wedge (h>1) \\ \Delta \overline{X}_{i} \text{ при } [f(\overline{X}_{i-1})\ge f(\overline{X}_{i})] \wedge [q(\overline{X}_{i})\ge 0] \\ -\Delta \overline{X}_{i+1} \text{ при } (|\Delta \overline{X}_{i}|\ne |\Delta \overline{X}_{i-1} |) \wedge (h\ge 1) \end{cases}$

где a —максимальная величина рабочего шага поиска;

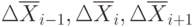$\overline{\zeta}_{i+1}$ — вектор случайных чисел; $\Delta \overline{X}_{i-1},\Delta \overline{X}_{i},\Delta \overline{X}_{i+1}$ — векторы приращений на (i-1)-, i-, (i+1) -м шагах поиска; $\overline{X}_{i},\overline{X}_{i+1},\overline{X}_{i+h}$ — векторы, описанные по формуле (1); $f(\overline{X}_{i-1}),f(\overline{X}_{i}),f(\overline{X}_{i+1})$ — значения критериев качества после осуществления на (i-1)-, i-, (i+1) -го шагов поиска.

Вектор случайных чисел

$\overline{\zeta}_{i+1}=(0,K,0,\zeta^{i+1}_k,K,\zeta^{i+1}_L,0,K,0)$

$\overline{\zeta}^{i+1}_{k}=\overline{\zeta}^{i+1}_{k+1}=\Lambda =\overline{\zeta}^{i+1}_{L}=\psi$

где $\psi$ — случайное равномерно распределенное число, выбираемое из интервала [-1, 1] ; k и L —случайные целые числа, распределенные на отрезке [1, n] и упорядоченные соотношением $k\le L$ .

Имеются и другие модификации этого алгоритма, которые могут оказаться более эффективными.

Некоторые замечания относительно использования ГА

Как можно заметить, ГА представляет собой смешанный алгоритм как для поиска глобального экстремума, так и для поиска локального. Это дает нам возможность упростить схему поиска глобально-оптимальных структур за счет использования в ней ГА как в качестве алгоритма СДС, так и в качестве алгоритма ШЛП. Каковы плюсы и минусы данной схемы? Плюсы — простота реализации, универсальность. Минусы — по сравнению со специальными алгоритмами СДС, которые будут давать нам гораздо больше жизнеспособных экземпляров, очень уменьшится скорость работы алгоритма. Таким образом, ГА предпочтительно использовать в следующих случаях: простые случаи, в которых программирование специального метода будет продолжаться гораздо дольше, чем поиск решения даже медленным методом; сложный случай, когда мы даже не знаем, с какой стороны подойти к задаче.

Интересно также отметить общие стороны ГА и алгоритма случайного поиска в подпространствах. Оба эти алгоритма при поиске оптимума изменяют не все возможные переменные, а только часть их. Это, казалось бы, мелкое усовершенствование ведет к поразительным результатам — эти алгоритмы в среднем дают трудоемкость нахождения решения на порядок ниже, чем метод сопряженных градиентов, и на два порядка ниже, чем метод случайного поиска по всему пространству переменных. Другими словами, эти алгоритмы используют одно из свойств нашего мира — независимость различных подсистем объектов.

Возвращаясь к основному вопросу данных лекций — интеллектуальным задачам, скажем, что данные алгоритмы ведут себя как опытные инженеры при поиске неисправностей (очень интеллектуальная по всем параметрам задача), и соблюдают заповедь — "никогда не трогать все сразу, только по очереди".

Дальше >>

Авторизоваться

Проектирование систем искусственного интеллекта

Машинная эволюция

Алгоритм поиска глобального экстремума

Алгоритм конкурирующих точек

Алгоритм случайного поиска в подпространствах

Некоторые замечания относительно использования ГА

Вопросы и ответы