Трехмерная графика с использованием Direct3D
При работе с матрицами следует учитывать, что преобразования масштабирования и вращения производятся относительно начала координат. Для комбинирования (умножения) двух матриц существует функция D3DXMatrixMultiply(), которая помещает результат перемножения двух матриц, которые передаются в качестве второго и третьего аргументов, в первый. К примеру, мы хотим повернуть объект вокруг оси Oy на угол 30 градусов и переместить его на вектор (1,2,3). Для этого можно воспользоваться правилом композиции двух элементарных преобразований с помощью матрицы поворота и матрицы перемещения.
| C++ |
D3DXMATRIX matRotY, matTrans, matRes; D3DXMatrixRotationY( &matRotY, 30*D3DX_PI/180 ); D3DXMatrixTranslation( &matTrans, 1, 2, 3 ); D3DXMatrixMultiply(&matRes, &matRotY, &matTrans); |
| Pascal |
var matRotY, matTrans, matRes: TD3XDMatrix; D3DXMatrixRotationY( matRotY, 30*pi/180 ); D3DXMatrixTranslation( matTrans, 1, 2, 3 ); D3DXMatrixMultiply( matRes, matRotY, matTrans ); |
Если поменять местами матрицы matRotY и matTrans в функции D3DXMatrixMultiply, то результат преобразования будет иной (сначала объект будет перемещен, а затем повернут). Вообще функция D3DXMatrixMultiply сама возвращает результат перемножения двух матриц, и поэтому ее можно использовать как параметр в матричных операциях. Ниже приведен пример такой возможности.
| C++ |
D3DXMATRIX matRotY, matTrans;
D3DXMatrixRotationY( &matRotY, … );
D3DXMatrixTranslation( &matTrans, … );
device->SetTransform(D3DTS_VIEW,
D3DXMatrixMultiply(NULL, &matRotY, &matTrans)); |
| Pascal |
var
matRotY, matTrans, matRes: TD3XDMatrix;
D3DXMatrixRotationY( matRotY, … );
D3DXMatrixTranslation( matTrans, … );
device.SetTransform(D3DTS_VIEW,
D3DXMatrixMultiply(nil, matRotY, matTrans)^); |
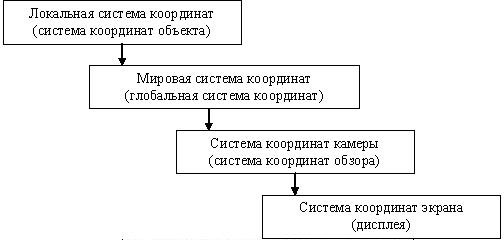
Для визуализации некоторого объекта (получение его проекции) нам необходимы следующие данные:
- Моделируемые объекты трехмерного мира (сцены);
- Положение виртуальной камеры, которая определяет перспективу.
В терминах систем координат процесс получения проекции может быть описан следующей упрощенной блок схемой:
Как известно из курса линейной алгебры, переход от одной системы координат к другой эквивалентен смене базиса. Когда нужно преобразовать объект из одного базиса в другой, нужно умножить все вершины объекта на соответствующую матрицу приведения базиса.
Библиотека Direct3D позволяет работать как в левосторонней системе координат, так и в правосторонней. Далее будем рассматривать все примеры для левосторонней системы координат.
Локальная система координат (локальное пространство) определяет исходные координаты объекта, т.е. в тех в которых он задан. Моделирование объекта в локальной (собственной) системе координат удобнее, чем напрямую в мировой системе координат. Локальная система позволяет описывать объект, не обращая внимания на положение, размер, ориентацию других объектов в мировой системе координат.
После того как заданы все объекты в своих собственных (локальных) системах координат, необходимо привязать их к общей мировой системе координат. Процесс трансформации координат объектов, заданных в локальных системах в мировую (общую) называют мировым преобразованием ( world transform ). Обычно используют 3 типа преобразований: перемещение, масштабирование, вращение. Мировое преобразование описывается с помощью матрицы, используя метод SetTransform интерфейса IDirect3DDevice9. Для применения мирового преобразования метод SetTransform вызывается с параметром D3DTS_WORLD. Предположим, что у нас в сцене присутствуют два объекта: куб и сфера. Мы собираемся отобразить куб в точке с координатами (-3, 2, 6), а сферу в точке (5, 0, -2) мировой системы координат. Это можно проделать с помощью следующих шагов.
| C++ |
D3DXMATRIX matCube, matSphere; D3DXMatrixTranslation(&matCube, -3.0f, 2.0f, 6.0f); pDirect3DDevice->SetTransform(D3DTS_WORLD, &matCube); drawCube(); D3DXMatrixTranslation(&matSphere, 5.0f, 0.0f, -2.0f); pDirect3DDevice->SetTransform(D3DTS_WORLD, &matSphere); drawSphere(); |
| Pascal |
var matCube, matSphere: TD3DXMatrix; … D3DXMatrixTranslation(matCube, -3.0, 2.0, 6.0); device.SetTransform(D3DTS_WORLD, matCube); drawCube; D3DXMatrixTranslation(matShpere, 5.0, 0.0, -2.0); device.SetTransform(D3DTS_WORLD, matSphere); drawSphere; |
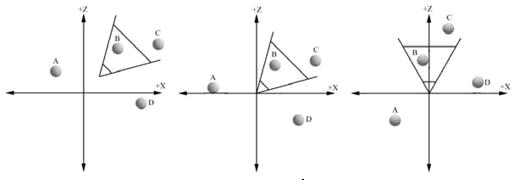
Построение проекции весьма сложная и очень неэффективная операция когда камера имеет произвольное положение и направление в мировой системе координат. Чтобы упростить эту ситуацию, мы перемещаем камеру в начало мировой системы координат и поворачиваем ее так, чтобы "взгляд" камеры был направлен в положительную сторону оси Z, как показано на рисунке ниже.
Матрица перехода в систему координат камеры может быть получена с помощью функции D3DXMatrixLookAtLH(), прототип которой показан ниже:
D3DXMatrixLookAtLH ( matView, // результат Eye, // положение камеры в мировой системе координат At, // точка в мировой системе, куда направлена камера (взгляд) Up // вектор, указывающий "где верх" в мировой системе координат ).
Для установки матрицы вида (преобразование в пространство камеры) используется метод SetTransform с первым параметром D3DTS_VIEW.