Трехмерная графика с использованием Direct3D
Принципы построения трехмерной сцены
В трехмерной графике пространственные объекты, заданные в непрерывном виде, как правило, аппроксимируют (приближают) множеством треугольников. Именно треугольник представляет собой элементарный примитив, с помощью которого описываются все элементы сцены, в том числе и те, которые имеют гладкую форму (сфера, цилиндр, параметрические поверхности и др.).
Процесс формирования изображения должен учитывать две главные сущности. Это визуализируемый объект сцены и наблюдатель. Объект существует в пространстве независимо от кого-либо. Наблюдатель же представляет собой средство формирования изображения наблюдаемых объектов. Именно наблюдатель формирует изображение. Наблюдатель и наблюдаемый объект существуют в одном и том же трехмерном мире, а создаваемое при этом изображение получается двухмерным. Суть процесса формирования изображения состоит в том, чтобы, зная положение наблюдателя и положение объекта, описать (синтезировать) получаемое при этом двухмерное изображение (проекцию).
В большинстве графических библиотек присутствуют следующие сущности трехмерной сцены:
- объекты;
- наблюдатель (камера);
- источники света;
- свойства материалов объекта.
При этом моделируемая трехмерная сцена может описываться тысячами, а иногда миллионами вершин. Для каждой вершины (точки) примитива должны выполняться вычисления по одним и тем же формулам.
Как мы знаем, точка в 3D графике задается, как правило, набором из 4-х значений (x,y,z,w). Реальные координаты точки в пространстве будут (x/w, y/w, z/w), компонент w является масштабом. Обычно для точек w=1. Вектор – направленный отрезок. Вектора равны если у них одинаковая длина и направление. Вектора также задаются в виде линейного массива 1х4 (x,y,z,w), но компонент w у векторов равен 0. Для выполнения преобразований с вершинами используют матричный подход. Матрица размерности MxN – прямоугольная таблица, имеющая M строк, N столбцов и заполненная элементами одного типа. В 3D графике используют, как правило, матрицы размерности 4х4. Таким образом преобразование точки в пространстве сводится к умножению вектор-строки размерности 4 на матрицу преобразования размером 4х4:
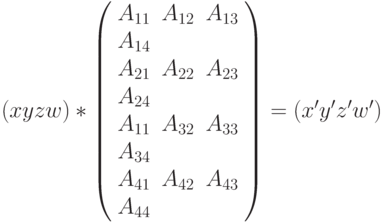
Так, например, умножение всех вершин объекта на одну из матриц вращения приведет к вращению этого объекта вокруг оси Ox, Oy или Oz соответственно. Для сложной трансформации объекта можно использовать последовательные преобразования, которые выражаются в перемножении (конкатенации) соответствующих матриц элементарных преобразований. Таким образом, можно сначала рассчитать единую (общую) матрицу преобразования (перемножить между собой все элементарные матрицы трансформации), а затем использовать только ее. Так, например, вращение объекта вокруг своей оси и одновременное движение по кругу определенного радиуса, может быть описано следующей последовательностью матриц: Vi *MatRot1(…)*MatTrans(…)*MatRot2(…), где Vi – координаты вершин объекта, MatRot1 – матрица поворота вокруг своей оси, MatTrans – матрица перемещения, MatRot2 – матрица вращения по кругу.
Вам не придется самостоятельно запоминать и вычислять все матрицы преобразования "вручную", т.к. во всех библиотеках 3D графики они предусмотрены. В библиотеке Direct3D определен матричный тип D3DXMATRIX – это структура, которая содержит 4х4 элементов.
Элемент матрицы с индексами ij указывает на значение, хранящееся в строке с номером i и столбце с номером j. Например, элемент _32 указывает на значение m[3][2]. Обращаться к элементам матрицы (читать, записывать) можно двумя способами.
| C++ |
D3DXMATRIX m; m._11 = …; или m.m[1][1] = …; |
| Pascal |
var m: TD3DXMatrix; … m._11 := …; или m.m[1,1] = …; |
Библиотека Direct3D содержит богатый набор процедур и функций по работе с матрицами. Приведем основные функции для работы с матрицами.
| C++ |
D3DXMATRIX m; // Создание единичной матрицы D3DXMatrixIdentity(&m); // Создание матрицы перемещения D3DXMatrixTranslation(&m, dx, dy, dz); // Создание матрицы масштабирования D3DXMatrixScaling(&m, kx, ky, kz); // Создание матриц вращения D3DXMatrixRotationX(&m, angleX); D3DXMatrixRotationY(&m, angleY); D3DXMatrixRotationZ(&m, angleZ); |
| Pascal |
var m: TD3DXMatrix; // Создание единичной матрицы D3DXMatrixIdentity(m); // Создание матрицы перемещения D3DXMatrixTranslation(m, dx, dy, dz); // Создание матрицы масштабирования D3DXMatrixScaling(m, kx, ky, kz); // Создание матриц вращения D3DXMatrixRotationX(m, angleX); D3DXMatrixRotationY(m, angleY); D3DXMatrixRotationZ(m, angleZ); |

