|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Временная стоимость денег
| Члены потока | Варианты погашения займа, тыс. руб. | ||
|---|---|---|---|
| возврат основного долга в конце срока | фиксированная выплата основного долга | фиксированная срочная уплата | |
| 1. Получение займа | +6000 | +6000 | +6000 |
| 2. Платеж в конце 1 года | -1200 | -3200 | -2848,4 |
| 3. Платеж в конце 2 года | -1440 | -2800 | -2848,4 |
| 4. Платеж в конце 3 года | -7728 | -2400 | -2848,4 |
| 5. Приведенная к моменту получения займа сумма выплат | -6472,2 | -6000 | -6000 |
Сравнивая между собой приведенные величины денежных притоков и оттоков по финансовой операции, определяют важнейший финансовый показатель чистая приведенная стоимость (NPV – от английского net present value). Наиболее общая формула определения этого показателя:
 |
( 1) |
где 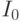 – первоначальные инвестиции в проект (оттоки денег),
– первоначальные инвестиции в проект (оттоки денег),
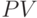 – приведенная стоимость будущих денежных потоков по проекту.
– приведенная стоимость будущих денежных потоков по проекту.
При использовании этой формулы все денежные притоки (доходы) обозначаются положительными цифрами, оттоки денежных средств (инвестиции, затраты) – отрицательными.
В нашем примере первоначально предприятие получало приток денежных средств (сумма займа 6 млн. рублей), а затем в течение 3 лет производило денежные расходы, т.е. оттоки средств. Поэтому к первоначальному моменту приводились не поступления, а затраты. Обычно при реализации инвестиционных проектов наблюдается обратная картина: сначала предприятие вкладывает средства, а затем получает периодические доходы от этих вложений. Поэтому, преобразуя (1) с учетом правил дисконтирования денежных потоков (формула (4) из предыдущей лекции), получаем:
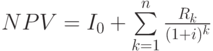 |
( 2) |
где  – общий срок финансовой операции (проекта),
– общий срок финансовой операции (проекта),
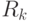 – элемент дисконтируемого денежного потока ( член ренты ) в периоде
– элемент дисконтируемого денежного потока ( член ренты ) в периоде  ,
,
 – номер периода.
– номер периода.
Под процентной ставкой  (в данном случае ее называют ставкой сравнения) понимается годовая сложная эффективная ставка декурсивных процентов. Срок операции
(в данном случае ее называют ставкой сравнения) понимается годовая сложная эффективная ставка декурсивных процентов. Срок операции  в общем случае измеряется в годах. Если же реальная операция не отвечает этим условиям, т.е. интервалы между платежами не равны году, то в качестве единицы измерения срока принимаются доли года, измеренные как правило в месяцах, деленных на 12. Например, инвестиции в сумме 500 тыс. рублей принесут в первый месяц 200 тыс. рублей дополнительного дохода, во второй 300 тыс. рублей и в третий – 700 тыс. рублей. Ставка сравнения равна 25%. Чистая приведенная стоимость данного проекта составит 1 млн. 147 тыс. руб.:
в общем случае измеряется в годах. Если же реальная операция не отвечает этим условиям, т.е. интервалы между платежами не равны году, то в качестве единицы измерения срока принимаются доли года, измеренные как правило в месяцах, деленных на 12. Например, инвестиции в сумме 500 тыс. рублей принесут в первый месяц 200 тыс. рублей дополнительного дохода, во второй 300 тыс. рублей и в третий – 700 тыс. рублей. Ставка сравнения равна 25%. Чистая приведенная стоимость данного проекта составит 1 млн. 147 тыс. руб.:
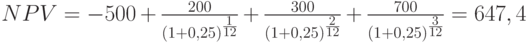
Довольно распространенной является ошибка, когда в подобных случаях пытаются рассчитать месячную процентную ставку делением годовой ставки на 12, а срок проекта измеряют в целых месяцах (вместо 1 / 12 года берут 1 месяц. вместо 2 / 12 – 2 и т.д.). В этом случае будет получен неправильный результат, т.к. возникнет эффект ежемесячного реинвестирования начисляемых сложных процентов. Чтобы получить эквивалентный результат, для нахождения месячной ставки необходимо предварительно пересчитать годовую эффективную ставку  в номинальную
в номинальную  при
при  по формуле
по формуле 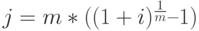 (см. гл. 2.2) . В данном случае эквивалентной является номинальная годовая ставка 22,52% ставка, разделив которую на 12 можно получить значение для помесячного дисконтирования денежного потока.
(см. гл. 2.2) . В данном случае эквивалентной является номинальная годовая ставка 22,52% ставка, разделив которую на 12 можно получить значение для помесячного дисконтирования денежного потока.
Если денежный поток состоит из одинаковых и равномерно рапределенных выплат (то есть представляет собой аннуитет ), можно упростить расчет NPV, воспользовавшись формулами дисконтирования аннуитетов из табл. 2.6 предыдущего параграфа. Например, если бы в рассматриваемом проекте было предусмотрено получение в течение трех месяцев по 400 тыс. рублей дохода ежемесячно (то есть 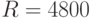 ), то следовало рассчитать приведенную стоимость аннуитета сроком 3 / 12 года и числом выплат
), то следовало рассчитать приведенную стоимость аннуитета сроком 3 / 12 года и числом выплат  . Применив формулу (12) из предыдущего параграфа, получим
. Применив формулу (12) из предыдущего параграфа, получим
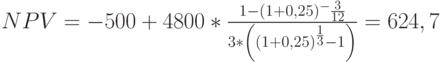
Кроме правильного вычисления чистой приведенной стоимости, необходимо понимать ее финансовый смысл. Положительное значение этого показателя указывает на финансовую целесообразность осуществления операции или реализации проекта. Отрицательная NPV свидетельствует об убыточности инвестирования капитала таким образом. В примере с проектом получено очень хорошее значение NPV, свидетельствующее о его инвестиционной привлекательности. Возвратившись к данным табл. 2.7, можно видеть, что два последних варианта погашения долга дают нулевую NPV, то есть в финансовом плане само по себе пользование заемными средствами не принесет предприятию ни вреда ни пользы. Если же оно изберет первый вариант (возврат основной суммы долга по окончании его срока), то получит отрицательную NPV –472,2 тыс. рублей, следовательно такой план погашения задолженности принесет ему финансовые потери.
О достоинствах и особенностях чистой приведенной стоимости будет очень подробно говориться в последующих лекциях. Остается только заметить, что значение ее для финансового менеджмента настолько высоко, что многократно окупает затраты труда по изучению и осмыслению всех вышеприведенных формул финансовых вычислений. Вторым столь же важным финансовым показателем является внутренняя норма доходности (IRR – от английского internal rate of return). Рассмотрим еще один инвестиционный проект. Внедрение новой технологии требует единовременных затрат в сумме 1,2 млн. рублей. Затем в течение 4 лет предприятие планирует получать дополнительный денежный поток от этих инвестиций в размере: 1-й год – 280 тыс. рублей, 2-й год – 750 тыс. рублей, 3-й год – 1 млн. рублей и 4-й год – 800 тыс. рублей. Рассчитаем NPV этого проекта при ставке сравнения 30% годовых:
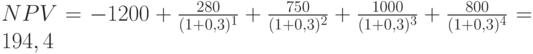
Реализация проекта может принести предприятию 194,4 тыс. рублей чистой приведенной стоимости при условии использования ставки сравнения 30%. А при какой процентной ставке проект будет иметь нулевую NPV, то есть, какой уровень доходности приравняет дисконтированную величину денежных притоков к сумме первоначальных инвестиций? Взглянув на формулу расчета NPV, можно сделать вывод, что увеличение ставки  снижает величину каждого члена потока и общую их сумму, следовательно, чем больше будет уровень ставки, приравнивающей NPV к нулю, тем более мощным будет сам положительный денежный поток. Иными словами, мы получаем характеристику финансовой эффективности проекта, которая как бы заложена внутри него самого. Поэтому данный параметр и получил название внутренняя норма доходности (иногда используется термин внутренняя норма рентабельности, внутренняя процентная ставка и др.). Итак IRR это такая годовая процентная ставка, которая приравнивает текущую стоимость денежных притоков по проекту к величине инвестиций, т.е. делает NPV проекта равным нулю.
снижает величину каждого члена потока и общую их сумму, следовательно, чем больше будет уровень ставки, приравнивающей NPV к нулю, тем более мощным будет сам положительный денежный поток. Иными словами, мы получаем характеристику финансовой эффективности проекта, которая как бы заложена внутри него самого. Поэтому данный параметр и получил название внутренняя норма доходности (иногда используется термин внутренняя норма рентабельности, внутренняя процентная ставка и др.). Итак IRR это такая годовая процентная ставка, которая приравнивает текущую стоимость денежных притоков по проекту к величине инвестиций, т.е. делает NPV проекта равным нулю.
Из определения IRR следует, что для ее расчета можно использовать формулу определения NPV (2), решив это уравнение относительно  . Однако данная задача не имеет прямого алгебраического решения, поэтому найти величину IRR можно или путем подбора значения или используя какой-либо итерационный способ (например, метод Ньютона-Рафсона). Широкое распространение вычислительной техники упростило решение подобных задач, поэтому в настоящем пособии не будет рассмотрен математический аппарат расчета IRR "вручную". Наличие ПК с пакетом электронных таблиц практически снимает проблему. Подберем с помощью компьютера значение
. Однако данная задача не имеет прямого алгебраического решения, поэтому найти величину IRR можно или путем подбора значения или используя какой-либо итерационный способ (например, метод Ньютона-Рафсона). Широкое распространение вычислительной техники упростило решение подобных задач, поэтому в настоящем пособии не будет рассмотрен математический аппарат расчета IRR "вручную". Наличие ПК с пакетом электронных таблиц практически снимает проблему. Подберем с помощью компьютера значение  , отвечающее заданным требованиям, оно составит около 37,9%. То есть данный инвестиционный проект обладает доходностью 37,9%. Сравнивая полученное значение с доходностью альтернативных проектов, можно выбрать наиболее эффективный из них.
, отвечающее заданным требованиям, оно составит около 37,9%. То есть данный инвестиционный проект обладает доходностью 37,9%. Сравнивая полученное значение с доходностью альтернативных проектов, можно выбрать наиболее эффективный из них.
