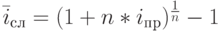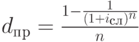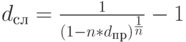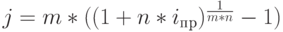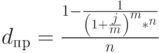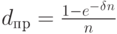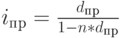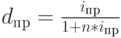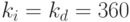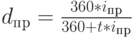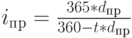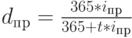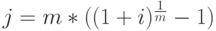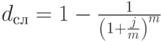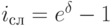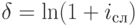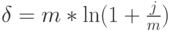Временная стоимость денег

Еще одним важнейшим параметром любой финансовой операции является процентная (учетная) ставка. Кроме технической функции, выполняемой этим показателем в ходе расчетов, он используется для оценки доходности – одного из фундаментальных понятий финансового менеджмента. Часто можно услышать (или прочитать) выражения, подобные следующим: "на этой сделке я заработал 50%" или "менеджеры нашего фонда обеспечат годовую доходность по Вашим вкладам не ниже 100%" и т.п. Следует сразу оговориться, что сами по себе эти выражения вполне корректны, однако объем содержащейся в них полезной информации значительно меньше, чем может показаться на первый взгляд. Из содержания предыдущей лекции можно сделать вывод, что любое упоминание о процентных ставках требует массу оговорок и уточнений. Попытаемся понять смысл первого выражения. Во-первых следует уточнить, к какому промежутку времени относится полученный доход – месяцу, году или длительности самой сделки. В последнем случае необходимо знать, чему равна эта длительность. Так как ничего не известно ни о сумме ни о длительности сделки, то ее результат "50% дохода" невозможно сравнить с доходностью какой-то другой операции, чтобы сделать вывод об уровне ее эффективности. Если в ответ на это выражение кто-нибудь заявит: "А я имею 25% годовых по своему банковскому депозиту", то определить, который же из этих двух инвесторов оказался более удачливым, будет практически невозможно.

Сталкиваясь с упоминанием о процентных ставках, финансист должен выяснить о каких процентах – простых или сложных, дискретных или непрерывных, – идет речь. Далее необходимо точно определиться с временной базой – рассчитываются ли годовые проценты или какие-то еще, если проценты годовые, то возникает вопрос, каким образом определяется длительность операции и продолжительность года. В случае начисления сложных процентов должно быть оговорено количество начислений процентов в течение года. В результате может оказаться, что методика определения доходности, используемая одним из контрагентов, не совпадает с той, что "принята на вооружение" другой стороной. Однако в этом уже не будет никакой трагедии, так как, зная особенности обеих этих методик, финансисты достаточно быстро приведут результаты своих расчетов в сопоставимый вид. То есть, своевременно задавая необходимые вопросы, финансист тем самым предотвращает возможные неприятные последствия использования несогласованных терминов. Вряд ли в обозримом будущем удастся заставить всех рассчитывать доходность по какой-либо единой методике, поэтому задача финансиста состоит не в том, чтобы вынудить своего контрагента применять единственный "правильный" способ, а в том, чтобы как можно скорее разобраться самому, что именно понимает под термином "доходность" его собеседник, и после этого решить, каким образом можно унифицировать расчеты. Вопросы определения доходности заслуживают отдельного разговора, поэтому здесь будут рассмотрены наиболее общие моменты расчета уровня процентных ставок в отдельных финансовых операциях и нахождения эквивалентных им значений.

Вначале рассмотрим способы расчета величины процентных (учетных) ставок, когда заданы другие параметры финансовой операции. Преобразовав формулы декурсивного и антисипативного наращения простых процентов, получим выражения (12) и (13) в табл. 2.1). Например, чему будет равна простая процентная ставка по ссуде, выданной на 90 дней в размере 350 тыс. рублей, и возвращенной по истечении срока в сумме 375 тыс. рублей (временная база 360 дней)? Подставив эти данные в формулу (12), получим:

Вексель номиналом 1 млн. рублей учтен в банке за 60 дней до его погашения в сумме 900 тыс. рублей. По какой простой учетной ставке было произведено его дисконтирование? Используем для расчетов формулу (13):

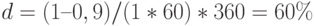
Очевидно, что даная методика может (и должна) использоваться при анализе любых финансовых операций, а не только в процессе банковского кредитования. Например, иностранная валюта в объеме 1000 единиц, купленная по курсу 20 руб. за 1 единицу, через месяц была продана по курсу 20 руб. 50 коп. Определить доходность этой операции по годовой простой процентной ставке ( коммерческие проценты ). Из формулы (12) получаем:

Аналогичный подход к расчету доходности используется и на фондовых рынках. Например, Центральным Банком России была рекомендована следующая формула расчета доходности ГКО:

( 14)

где – номинал облигации;

– цена ее приобретения;

– срок до погашения.

По сути дела она повторяет формулу (12) применительно к точным процентам (временная база 365 дней). Например, облигация номиналом 10 тыс. рублей была приобретена за 8,2 тыс. рублей за 40 дней до погашения. Ее годовая доходность, рассчитанная как простая процентная ставка, составит:

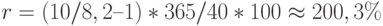
Точно такой же результат можно получить, применив формулу (12).

Не следует отождествлять процентную ставку, указываемую в кредитном договоре, с доходностью операции, рассчитанной в процентах. В первом случае процентная ставка является реальным параметром финансовой операции, однозначно определяющим величину платежа, который должен последовать в случае исполнения договора. Доходность же – это производная величина, не определяющая, а определяемая теми денежными потоками, которые порождает кредитный договор (ценная бумага или другой финансовый инструмент). В первой лекции данного курса подчеркивался абстрактный характер понятия "прибыль предприятия". То же самое можно сказать о доходности – в явной форме она не присутствует в ходе осуществления финансовой операции. Рассчитывая доходность финансовой операции, инвестор получает субъективную оценку ее величины, зависящую от целого ряда предпосылок, таких как способ начисления процентов, выбор временной базы и т.п. Эти предпосылки не являются объективными и неизбежными – при всем уважении к Центральному банку инвестор может определить доходность купленной им ГКО по ставке сложных, а не простых процентов, не нарушив при этом ни физических ни юридических законов (и поступив совершенно правильно с позиции финансовой теории).

Рекомендация вычислять доходность по методике наращения простых процентов используется на данном рынке как соглашение его участников (точно такое же как соглашение о подсчете точной временной базы). Выполнение условий этого соглашения гарантирует участникам рынка сопоставимость результатов их расчетов, т.е. помогает избежать путаницы, но не более этого. Степень соответствия того либо иного метода расчета доходности идеалу в данном контексте не имеет значения – это предмет научных дискуссий. Используя неправильную или несовершенную методику расчета доходности, инвестор имеет все шансы достаточно быстро разориться, точно так же как и предприятие, завышающее прибыль, вследствие неправильного калькулирования издержек. Но конечной причиной банкротства станет отсутствие у него денег для покрытия обязательств, до этого момента ни один кредитор не сможет вчинить иск о банкротстве только на основании несогласия с методикой подсчета доходности, которой пользуется его должник.

Для финансового менеджмента сложные проценты имеют неизмеримо большую ценность, чем простые. Очевидно, что при использовании методики расчета простых процентов значение доходности искажается уже из-за того, что данная методика не учитывает возможности реинвестирования полученных доходов. Пэтому при прочих равных условиях безусловно предпочтительным является расчет доходности как ставки сложных процентов. Рассмотрим методику определения величины этой ставки, когда известны другие параметры финансовой операции. В результате преобразования исходных выражений наращения ( дисконтирования ) по сложным процентам, получим (см. (15) – (19) в табл. 2.1).

В качестве иллюстрации рассчитаем доходность облигации из предыдущего примера как ставку сложного процента (наращение 1 раз в году):

Этот результат более чем в 2,5 раза превышает доходность, рассчитанную как ставку простых процентов. Означает ли это, что инвестор, использующий для расчета доходности сложные проценты, в два с половиной раза богаче того, кто купив в один день с ним точно такую же облигацию, применяет для вычислений простые проценты? Тогда последнему следует срочно разучивать новую формулу и точно так же богатеть.

Однако, в случае сложных процентов не все так однозначно. Если рассчитывать доходность как сложную номинальную ставку (16), то ее уровень резко снизится, при получим:

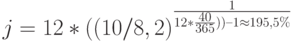
При расчете доходности как силы роста – непрерывные проценты (19) – ее уровень будет более точно соответствовать тому, что был рассчитан с помощью простой процентной ставки:

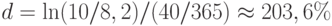
Чтобы не запутаться в обилии методов расчета процентных ставок не обязательно зазубривать каждую формулу. Достаточно четко представлять, каким образом она получена. Кроме этого, следует помнить, что любому значению данной ставки может быть поставлено в соответствие эквивалентное значение какой-либо другой процентной или учетной ставки. В предыдущей лекции был приведен подобный пример эквивалентности между простыми процентной и учетной ставками (5). Эквивалентными называются ставки, наращение или дисконтирование по которым приводит к одному и тому же финансовому результату. Например, в условиях последнего примера эквивалентными являются простая процентная ставка 200,3% и сложная процентная ставка 511,6%, т.к. начисление любой из них позволяет нарастить первоначальную сумму 8,2 тыс. рублей до 10 тыс. рублей за 40 дней. Приравнивая между собой множители наращения ( дисконтирования ), можно получить несложные формулы эквивалентности различных ставок. Для удобства эти формулы представлены в табличной форме. В заголовки граф табл. 2.2 помещены простые процентная ( ) и учетная ( ) ставки. В заголовках строк этой таблицы указаны все рассмотренные в данном пособии ставки. На пересечении граф и столбцов приводятся формулы эквивалентности соответствующих ставок. В таблицу не включены уравнения эквивалентности простых процентных и сложных учетных ставок, вследствие маловероятности возникновения необходимости в таком сопоставлении.

Знание уравнений эквивалентности позволяет без труда переходить от одного измерения доходности к другому. Например, доходность облигаций по простой процентной ставке составила за полгода 60%. По формуле (21) найдем, что в пересчете на сложные проценты это составляет 69%. Доходность векселя, дисконтированного по простой учетной ставке 50% за 3 месяца до срока погашения, в пересчете на простую процентную ставку составит 57,14% (34), если же по процентной ставке принята точная временная база (365 дней), то применив формулу (36), получим = 57,94%).

Таблица 2.2. Эквивалентность простых ставок

	Простая процентная ставка ( )	Простая учетная ставка ( )
Сложная процентная ставка ( )	( 20) ( 21)	( 22) ( 23)
Сложная номинальная процентная ставка ( )	( 24) ( 25)	( 26) ( 27)
Сила роста ( )	( 28) ( 29)	( 30) ( 31)
Простая учетная ставка ( )	( 32) ( 33)	-
Простая учетная ставка ( )	( 34) ( 35)	-
Простая учетная ставка ( )	( 36) ( 37)	-

Например, предприятие может столкнуться с необходимостью выбора между получением кредита на 5 месяцев под сложную номинальную ставку 24% (начисление процентов поквартальное) и учетом в банке векселя на эту же сумму и с таким же сроком погашения. Небходимо определить простую учетную ставку, которая сделает учет векселя равновыгодной операцией по отношению к получению ссуды. По формуле (26) получим .

Кроме формул, приведенных в табл. 2.2 и 2.3, следует отметить еще одно полезное соотношение. Между силой роста и дисконтным множителем декурсивных процентов существует следующая связь:

( 38)

По мере усложнения задач, стоящих перед финансовым менеджментом, сфера применения непрерывных процентов будет расширяться, так как при этом становится возможным использовать более мощный математический аппарат. Особенно наглядно это проявляется в случае непрерывных процентных ставок. В обыденной практике финансистов данный способ пока еще не занял должного места, что в какой-то мере объясняется его непривычностью, может быть чересчур "отвлеченным" характером. Однако трезвый анализ показывает, что предположение о непрерывности реинвестирования начисленных процентов не такое уж абстрактное и нереальное. В самом деле, как для простых, так и для сложных процентов факт непрерывности их начисления ни у кого не вызывает сомнений (годовая ставка 36% означает 3% в месяц, 0,1% в день и т.д., то есть можно начислять проценты хоть за доли секунды). Но точно такой же аксиомой для финансов является признание возможности мгновенного реинвестирования любых полученных сумм. Что же мешает совместить два этих предположения? В теории сумма начисленных процентов может (и должна) реинвестироваться сразу по мере ее начисления, т.е. непрерывно. В данном утверждении ничуть не меньше логики, чем в предположении, что реинвестирование должно производиться дискретно. Почему реинвестирование 1 раз в год считается более "естественным" чем 12 или 6 раз? Почему эта периодичность привязывается к календарным периодам (год, квартал, месяц), почему нельзя реинвестировать начисленные сложные проценты, скажем 39 раз в год или 666 раз за период между двумя полнолуниями? На все эти вопросы ответ, скорее всего, будет один – так сложилось, так привычно, так удобнее. Но выше уже было отмечено, что практический расчет величины реальных денежных потоков (например, дивидендных или купонных выплат) и определение доходности финансовых операций это далеко не одно и то же. Если привычнее и удобнее выплачивать купон по облигации 2 раза в год, то так и следует поступать. Но, определять доходность этой операции более логично по ставке непрерывных процентов.

Таблица 2.3. Эквивалентность сложных процентных ставок

	Сложная процентная ставка ( )	Сложная учетная ставка ( )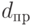
Сложная номинальная процентная ставка ( )	( 39) ( 40)	( 41) ( 42)
Сила роста ( )	( 43) ( 44)	( 45) ( 46)
Сложная учетная ставка ( )	( 47) ( 48)	-

Например, по вкладу в размере 10 тыс. рублей начисляется 25 простых процентов в год. В конце 1 года вклад возрастет до 12500 рублей. Доходность, измеренная как по простой (формула 12), так и сложной (15) процентной ставке i, составит 25% годовых. Однако, измеряя доходность по номинальной ставке (16) при m = 2, получим лишь 23,61%, т.к. в этом случае будет учтена потерянная вкладчиком возможность реинвестирования процентов хотя бы 2 раза в год. Если же измерить доходность по силе роста (19), то она окажется еще ниже – всего 22,31%, т.к. теоретически он мог реинвестировать начисленные проценты не 2 раза в год, а непрерывно.