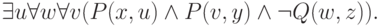|
Это в лекции 3. |
Язык логики предикатов
Эквивалентные формулы и нормальные формы
С понятием эквивалентности формул мы уже знакомились, когда рассматривали булевы формулы (формулы логики высказываний). Для логики предикатов эквивалентность определяется следующим образом.
Определение 7.10. Формулы  и
и  сигнатуры
сигнатуры  называются эквивалентными, если для любой системы
называются эквивалентными, если для любой системы 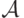 этой сигнатуры и любого ее состояния
этой сигнатуры и любого ее состояния  имеет место равенство
имеет место равенство  .
В этом случае пишем
.
В этом случае пишем  .
.
Отметим сначала, что все эквивалентности булевых формул, приведенные
в
"лекции 4"
: законы ассоциативности и коммутативности
для конъюнкции и дизъюнкции, законы дистрибутивности, двойного отрицания,
де Моргана и др., остаются справедливыми и для формул логики предикатов.
Поэтому и для них мы примем соглашение об упрощенной записи, которое позволяет опускать
скобки в формулах, содержащих только операции конъюнкции или только
операции дизъюнкции. Разрешим также опускать внешние скобки в формулах,
внешняя функция которых 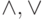 или
или 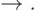 Например, формула
Например, формула 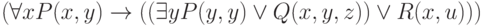 может быть упрощенно записана как
может быть упрощенно записана как 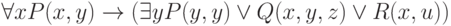 .
.
Для логики предикатов остается справедливым и правило замены эквивалентных подформул:
если  является подформулой формулы
является подформулой формулы 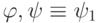 и формула
и формула 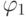 получена из формулы
получена из формулы  заменой некоторого вхождения
заменой некоторого вхождения  на
на  , то
, то 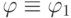 .
.
Доказательство этого правила получается индукцией по определению значения формулы на состоянии системы (см. задачу 7.8).
Новые эквивалентности связаны с кванторами.
Теорема 7.1. Для любых формул 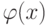 и
и  таких, что
таких, что  не содержит свободно переменной x,
имеют место следующие эквивалентности.
не содержит свободно переменной x,
имеют место следующие эквивалентности.
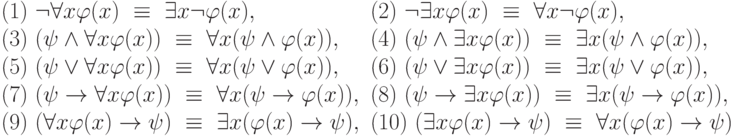
Доказательства всех этих эквивалентностей получаются непосредственно
из определения значения формул на состояниях. Рассмотрим, например, первую из них.
Для любого состояния  имеем
имеем  .
Это значение
равно 1 тогда и только тогда, когда
.
Это значение
равно 1 тогда и только тогда, когда 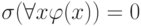 или, по определению значения квантора
или, по определению значения квантора 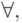 когда найдется такое состояние
когда найдется такое состояние 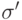 , совпадающее с
, совпадающее с  вне x,
для которого
вне x,
для которого  . Но это эквивалентно истинности формулы
. Но это эквивалентно истинности формулы 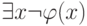 на состоянии
на состоянии 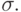
Рассмотрим еще эквивалентности (9) и (10), которые, на первый взгляд, могут удивить - квантор всеобщности превращается при вынесении за скобки в квантор существования и наоборот. Доказательство (9) получается с помощью булевых эквивалентностей и пунктов (1) и (4) настоящей теоремы:
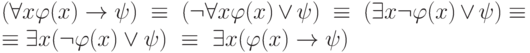
Эквивалентность (10) доказывается аналогично.
Останутся ли эквивалентности (2) - (8) справедливыми, если мы
не будем требовать, чтобы формула  не содержала свободных
вхождений переменной x? Нет! Рассмотрим, например, для арифметической
сигнатуры две формулы
не содержала свободных
вхождений переменной x? Нет! Рассмотрим, например, для арифметической
сигнатуры две формулы 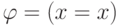 и
и  . Тогда формула
. Тогда формула 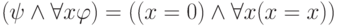 , представляющая
левую часть эквивалентности (3) истинна на состоянии
, представляющая
левую часть эквивалентности (3) истинна на состоянии  в котором
$
в котором
$  (x)=0.$ А формула
(x)=0.$ А формула 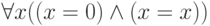 , представляющая
ее правую часть, ложна на всех состояниях.
Чтобы корректно вынести за скобки квантор в формуле
, представляющая
ее правую часть, ложна на всех состояниях.
Чтобы корректно вынести за скобки квантор в формуле  ,
в которой
,
в которой 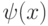 содержит x свободно, нужно предварительно переименовать связанную переменную в
содержит x свободно, нужно предварительно переименовать связанную переменную в 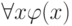 . Это позволяют сделать следующие эквивалентности, справедливость которых следует из предложения 7.1.
. Это позволяют сделать следующие эквивалентности, справедливость которых следует из предложения 7.1.
Лемма 7.1.О замене связанных переменных.
-
 , где
, где 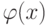 не содержит y, а
не содержит y, а 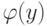 получается заменой всех свободных вхождений x в
получается заменой всех свободных вхождений x в 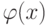 на y.
на y. -
 , где
, где 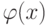 не содержит y, а
не содержит y, а 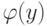 получается заменой всех свободных вхождений x в
получается заменой всех свободных вхождений x в 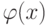 на y.
на y.
Используя эту лемму, можем получить следующую цепочку эквивалентностей:  . В общем случае, если переменная y не входит в
. В общем случае, если переменная y не входит в 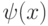 и в
и в 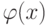 ,
справедлива эквивалентность
,
справедлива эквивалентность  .
.
Определение 7.11.
Формула вида 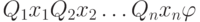 , где
, где  - бескванторная формула,
а каждый символ Qi - это один из кванторов
- бескванторная формула,
а каждый символ Qi - это один из кванторов 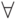 или
или 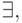 называется предваренной (или пренексной) нормальной формой.
Последовательность кванторов Q1 x1 Q2 x2 ... Qn xn называется ее приставкой, а бескванторная формула
называется предваренной (или пренексной) нормальной формой.
Последовательность кванторов Q1 x1 Q2 x2 ... Qn xn называется ее приставкой, а бескванторная формула  -
матрицей этой нормальной формы.
-
матрицей этой нормальной формы.
Теорема 7.2. О предваренной форме.
Для всякой формулы  существует формула
существует формула  в предваренной нормальной форме такая, что
в предваренной нормальной форме такая, что  .
.
Доказательство следует из теоремы 7.1 и леммы 7.1. Мы приведем его
в виде процедуры, которая позволяет построить предваренную форму  по исходной
формуле
по исходной
формуле 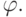 Процедура состоит из двух этапов.
На первом этапе, используя лемму 7.1, заменим все связанные переменные в
Процедура состоит из двух этапов.
На первом этапе, используя лемму 7.1, заменим все связанные переменные в  на новые так, чтобы
на новые так, чтобы
- разные кванторы связывали разные переменные и
- имена всех связанных переменных не пересекались с именами свободных переменных
- формулы
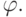
На втором этапе используя эквивалентности (3) - (10) теоремы 7.1 поочередно выносим
кванторы за скобки. Именно, последовательно заменяем каждую подформулу вида 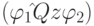 , где
, где  на эквивалентную формулу
на эквивалентную формулу 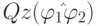 , и каждую подформулу вида
, и каждую подформулу вида 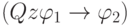 на формулу
на формулу 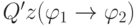 ,
где
,
где  при
при 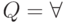 и
и  при
при 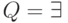 . Если после этого вынесенный квантор стоит сразу после операции отрицания
. Если после этого вынесенный квантор стоит сразу после операции отрицания 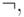 то, применяя эквивалентности (1), (2), проносим
отрицание в глубь формулы. Заметим, что порядок выноса кванторов определен неоднозначно,
в зависимости от него в результате могут получиться эквивалентные формулы с разными кванторными
приставками.
то, применяя эквивалентности (1), (2), проносим
отрицание в глубь формулы. Заметим, что порядок выноса кванторов определен неоднозначно,
в зависимости от него в результате могут получиться эквивалентные формулы с разными кванторными
приставками.
Пример 7.1.
Рассмотрим пример. Пусть 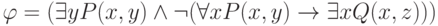 .
.
Ее свободные переменные: x, y и z (у x и y имеются также и связанные вхождения).
Выберем в качестве новых имен для связанных переменных u, v и w и заменим ими
"старые" связанные переменные. Получим эквивалентную формулу  .
На следующем этапе выносим кванторы за скобки (в качестве индексов у знаков эквивалентности
указаны номера применяемых эквивалентностей):
.
На следующем этапе выносим кванторы за скобки (в качестве индексов у знаков эквивалентности
указаны номера применяемых эквивалентностей):
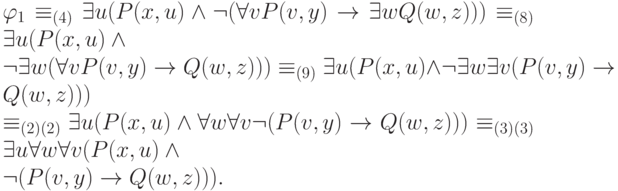
Далее можно упрощать матрицу формулы, используя известные эквивалентности булевой логики. В данном случае получим формулу