Эквивалентность формул и нормальные формы

Сокращенные ДНФ

Сокращенные ДНФ являются еще одним способом однозначного представления булевых функций, которое во многих случаях может оказаться более простым, чем представление с помощью совершенных ДНФ.

Напомним, что мы рассматриваем булевы функции над переменными 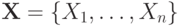. С каждой элементарной конъюнкцией связано множество наборов переменных, на которых K принимает значение 1. Нетрудно понять, что это множество содержит 2_(n-k) наборов, в которых каждая из входящих в K переменных имеет фиксированное значение 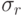, а значения остальных (n-k) переменных произвольны.

Определение Пусть f - произвольная булева функция над . Элементарная конъюнкция K называется допустимой для f, если .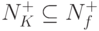

Элементарная конъюнкция K называется максимальной для f, если для любой элементарной конъюнкции L из условия 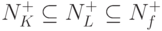следует, что .

Сокращенной ДНФ для функции f называется дизъюнкция всех максимальных для этой функции элементарных конъюнкций .

Из этого определения непосредственно следует, что сокращенная ДНФ для функции f единственна (с точностью до порядка элементарных конъюнкций и порядка переменных в них) и в точности задает функцию f.

Примером сокращенной ДНФ является формула 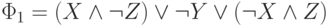из примера 4.1.

Сокращенную ДНФ можно получить из произвольной ДНФ D, используя процедуру, называемую методом Блейка.

1. Применять, сколько возможно, закон поглощения

   (П3):

   слева направо при условии, что конъюнкция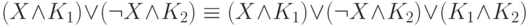 непротиворечива, т.е. не содержит одновременно некоторую переменную и ее отрицание. (Заметим, что на этом этапе число элементарных конъюнкций в ДНФ, вообще говоря, увеличивается).
2. Применять, сколько возможно, правило поглощения

   (П1): .

   Затем удалить повторные вхождения конъюнкций.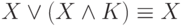

Теорема 4.2. В результате применения метода Блейка к произвольной ДНФ через конечное число шагов будет получена эквивалентная ей сокращенная ДНФ.

Доказательство Пусть после (1)-го этапа процедуры ДНФ D функции f преобразовалась в эквивалентную ДНФ D₁ . Покажем, что для всякой допустимой для f элементарной конъюнкция K в D₁ найдется такая конъюнкция K', что . Доказательство проведем возвратной индукцией по числу переменных в K.

Базис индукции. Пусть K содержит все n переменных из . Тогда состоит из единственного набора и, поскольку 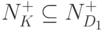, то в 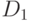сущетсвует конъюнкция K', для которой .

Шаг индукции. Пусть для некоторого k < n утверждение верно для всех допустимых для f конъюнкций, содержащих не менее (k+1) -ой переменной. Докажем, что оно верно и для допустимых конъюнкций с k переменными.

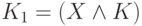Пусть допустимая для f элементарная конъюнкция K содержит k переменных и пусть - переменная, не входящая в K. Тогда обе элементарные конъюнкции и 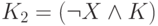являются допустимыми для f и по предположению индукции для них в 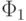найдутся такие и , что и 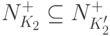. Если хотя бы одна из них не содержит X, то ее можно выбрать в качестве K'. В противном случае, их можно представить в виде 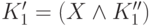и 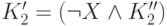. При этом 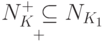и . Поскольку все преобразования вида (П3) выполнены, то D₁ тогда содержит и конъюнкцию 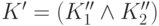, для которой .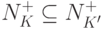

Заметим, что если K максимальна для f, то 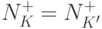. Таким образом, все максимальные конъюнкции входят в D₁ .

Теперь, чтобы завершить доказательство теоремы, нужно показать, что на этапе (2) из D₁ будут удалены все немаксимальные элементарные конъюнкции. (Докажите это индукцией по числу немаксимальных конъюнкций в D₁ .)

Пример 4.2. Применим метод Блейка к совершенной ДНФ функции f(X₁,X₂,X₃) , принимающей значение 1 на наборах множества .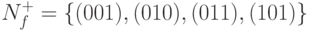

Ее совершенная ДНФ .

После применения преобразований (П3) на (1)-ом этапе получим

После поглощений (П1) на втором этапе останется сокращенная ДНФ

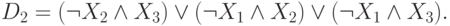
Заметим, что она не является самой короткой ДНФ для f, т.к. .
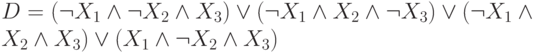