Методы сжатия изображений
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 10.10.2007 | Доступ: свободный | Студентов: 1478 / 158 | Оценка: 4.36 / 4.18 | Длительность: 14:22:00
Темы: Компьютерная графика, Алгоритмы и дискретные структуры
Специальности: Программист
Теги: I-MPEG, JPEG, mpeg, ppm, RLE, u-кадры, алгоритмы, алфавит, архивация, видео, графика, декодирование, кодер, моделирование, нормализация, поиск, потоки, приложения, сжатие, стандарты, форматы, цвета, элементы
Лекция 7:

Алгоритмы сжатия изображений
A
|
версия для печати
< Лекция 6 || Лекция 7: 12345 || Лекция 8 >

Для сжатия без потерь коэффициенты представлены в табл. 7.3

Таблица 7.3.
  При упаковке При распаковке
i Низкочастотные коэффициенты {\rm{h}}_{\rm{L}} {\rm{(i)}} Высокочастотные коэффициенты {\rm{h}}_{\rm{H}} {\rm{(i)}} Низкочастотные коэффициенты 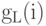{\rm{g}}_{\rm{L}} {\rm{(i)}} Высокочастотные коэффициенты {\rm{g}}_{\rm{H}} {\rm{(i)}}
0 6/8 1 1 6/8
±1 2/8 -1/2 1/2 -2/8
±2 -1/8 0 0 -1/8

Само преобразование в одномерном случае представляет собой скалярное произведение коэффициентов фильтра на строку преобразуемых значений (в нашем случае - на строку изображения). При этом четные выходящие значения формируются с помощью низкочастотного преобразования, а нечетные с помощью высокочастотного:

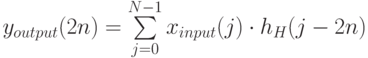
y_{output} (2n) = \sum\limits_{j = 0}^{N - 1} {x_{input} (j) \cdot h_H (j - 2n)}

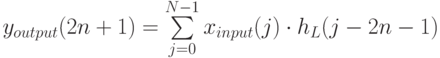
y_{output} (2n + 1) = \sum\limits_{j = 0}^{N - 1} {x_{input} (j) \cdot h_L (j - 2n - 1)}

Поскольку большинство {\rm{h}}_{\rm{L}} {\rm{(i)}}, кроме окрестности i=0, равны 0, то можно переписать приведенные формулы с меньшим количеством операций. Для простоты рассмотрим случай сжатия без потерь.

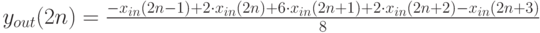
y_{out} (2n) = {{ - x_{in} (2n - 1) + 2 \cdot x_{in} (2n) + 6 \cdot x_{in} (2n + 1) + 2 \cdot x_{in} (2n + 2) - x_{in} (2n + 3)} \over 8}

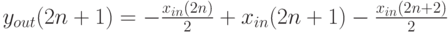
y_{out} (2n + 1) = - {{x_{in} (2n)} \over 2} + x_{in} (2n + 1) - {{x_{in} (2n + 2)} \over 2}

Легко показать, что данную запись можно эквивалентно переписать, уменьшив еще втрое количество операций умножения и деления (однако теперь необходимо будет подсчитать сначала все нечетные y ). Добавим также операции округления до ближайшего целого, не превышающего заданное число а, обозначаемые как 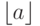\left\lfloor a \right\rfloor :

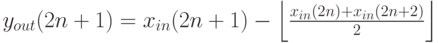
y_{out} (2n + 1) = x_{in} (2n + 1) - \left\lfloor {{{x_{in} (2n) + x_{in} (2n + 2)} \over 2}} \right\rfloor

y_{out} (2n) = x_{in} (2n) + \left\lfloor {{{y_{out} (2n - 1) + y_{out} (2n + 1) + 2} \over 4}} \right\rfloor

Упражнение: Самостоятельно уменьшите количество операций для случая без потерь.

Рассмотрим на примере, как работает данное преобразование. Для того, чтобы преобразование можно было применять к крайним пикселам изображения, оно симметрично достраивается в обе стороны на несколько пикселов, как показано на рис. 7.4. В худшем случае (сжатие с потерями) нам необходимо достроить изображение на 4 пиксела.

Симметричное расширение изображения (яркости АБ…Е) по строке вправо и влево

Рис. 7.4. Симметричное расширение изображения (яркости АБ…Е) по строке вправо и влево

Пусть мы преобразуем строку из 10 пикселов. Расширим ее значения вправо и влево и применим DWT преобразование:


Получившаяся строка 1, 0, 3, 1, 11, 4, 13, -2, 8, -5 и является цепочкой, однозначно задающей исходные данные. Совершив аналогичные преобразования с коэффициентами для распаковки, приведенными выше в таблице, получим необходимые формулы:

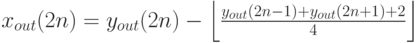
x_{out} (2n) = y_{out} (2n) - \left\lfloor {{{y_{out} (2n - 1) + y_{out} (2n + 1) + 2} \over 4}} \right\rfloor

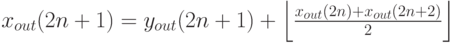
x_{out} (2n + 1) = y_{out} (2n + 1) + \left\lfloor {{{x_{out} (2n) + x_{out} (2n + 2)} \over 2}} \right\rfloor

Упражнение: Докажите, что во всех случаях округления мы будем получать одинаковые входную и выходную цепочки.

Легко проверить (используя преобразование упаковки), что значения на концах строк в yout также симметричны относительно n =0 и 9. Воспользовавшись этим свойством, расширим нашу строку вправо и влево и применим обратное преобразование:


Как видим, мы получили исходную цепочку ( 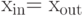{\rm{x}}_{{\rm{in}}} {\rm{ = x}}_{{\rm{out}}} ).

Упражнение: Примените прямое и обратное DWT -преобразования к цепочке из 10 байт:

121, 107, 98, 102, 145, 182, 169, 174, 157, 155.

Далее к строке применяется чересстрочное преобразование, суть которого заключается в том, что все четные коэффициенты переписываются в начало строки, а все нечетные - в конец. В результате этого преобразования в начале строки формируется "уменьшенная копия" всей строки (низкочастотная составляющая), а в конце строки - информация о колебаниях значений промежуточных пикселов (высокочастотная составляющая).


Это преобразование применяется сначала ко всем строкам изображения, а затем ко всем столбцам изображения. В результате изображение делится на 4 квадранта (примеры смотрите в описании рекурсивного сжатия). В первом квадранте будет сформирована уменьшенная копия изображения, а в остальных трех - высокочастотная информация. После чего преобразование повторно применяется уже только к первому квадранту изображения по тем же правилам (рис. 7.5).


Рис. 7.5.

Для корректного сохранения результатов под данные 2 и 3 квадрантов выделяется на один бит больше, а под данные 4-го квадранта - на 2 бита больше. Т.е. если исходные данные были 8-битные, то на 2 и 3 квадранты нужно 9 бит, а на 4-й - 10, независимо от уровня применения DWT. При записи коэффициентов в файл можно использовать иерархическую структуру DWT, помещая коэффициенты преобразований с большего уровня в начало файла. Это позволяет получить "изображение для предварительного просмотра", прочитав небольшой участок данных из начала файла, а не распаковывая весь файл, как это приходилось делать при сжатии изображения целиком. Иерархичность преобразования может также использоваться для плавного улучшения качества изображения при передаче его по сети.

Шаг 4.

Так же, как и в алгоритме JPEG, после DWT применяется квантование. Коэффициенты квадрантов делятся на заранее заданное число. При увеличении этого числа снижается динамический диапазон коэффициентов, они становятся ближе к 0, и мы получаем большую степень сжатия. Варьируя эти числа для разных уровней преобразования, для разных цветовых компонент и для разных квадрантов, мы очень гибко управляем степенью потерь в изображении. Рассчитанные в компрессоре оптимальные коэффициенты квантования передаются в декомпрессор для однозначной распаковки.

Шаг 5.

Для сжатия получающихся массивов данных в JPEG 2000 используется вариант арифметического сжатия, называемый MQ-кодер, прообраз которого ( QM-кодер ) рассматривался еще в стандарте JPEG, но реально не использовался из-за патентных ограничений. Подробнее об алгоритме арифметического сжатия читайте в соответствующей главе раздела.

Дальше >>
< Лекция 6 || Лекция 7: 12345 || Лекция 8 >

Вопросы и ответы

вопросов: 0