Алгоритмы сжатия изображений
Рекурсивный (волновой) алгоритм
Английское название рекурсивного сжатия - wavelet. На русский язык оно переводится как волновое сжатие, как сжатие с использованием всплесков, а в последнее время и калькой вэйвлет-сжатие. Этот вид архивации известен довольно давно и напрямую исходит из идеи использования когерентности областей. Ориентирован алгоритм на цветные и черно-белые изображения с плавными переходами. Идеален для картинок типа рентгеновских снимков. Степень сжатия задается и варьируется в пределах 5-100. При попытке задать больший коэффициент на резких границах, особенно проходящих по диагонали, проявляется "лестничный эффект" - ступеньки разной яркости размером в несколько пикселов.
Идея алгоритма заключается в том, что мы сохраняем в файл разницу - число между средними значениями соседних блоков в изображении, которая обычно принимает значения, близкие к 0.
Так два числа  и
и  всегда можно представить в виде
всегда можно представить в виде  и
и 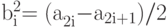 . Аналогично последовательность
. Аналогично последовательность 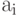 может быть попарно переведена в последовательность
может быть попарно переведена в последовательность  .
.
Разберем конкретный пример: пусть мы сжимаем строку из 8 значений яркости пикселов
( 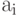 ): (220, 211, 212, 218, 217, 214, 210, 202). Мы получим следующие последовательности
): (220, 211, 212, 218, 217, 214, 210, 202). Мы получим следующие последовательности 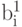 , и
, и  : (215.5, 215, 215.5, 206) и (4.5, -3, 1.5, 4). Заметим, что значения
: (215.5, 215, 215.5, 206) и (4.5, -3, 1.5, 4). Заметим, что значения 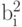 достаточно близки к 0. Повторим операцию, рассматривая
достаточно близки к 0. Повторим операцию, рассматривая  как
как 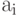 . Данное действие выполняется как бы рекурсивно, откуда и название алгоритма. Мы получим из (215.5, 215, 215.5, 206): (215.25, 210.75) (0.25, 4.75). Полученные коэффициенты, округлив до целых и сжав, например, с помощью алгоритма Хаффмана с фиксированными таблицами, мы можем поместить в файл.
. Данное действие выполняется как бы рекурсивно, откуда и название алгоритма. Мы получим из (215.5, 215, 215.5, 206): (215.25, 210.75) (0.25, 4.75). Полученные коэффициенты, округлив до целых и сжав, например, с помощью алгоритма Хаффмана с фиксированными таблицами, мы можем поместить в файл.
Заметим, что мы применяли наше преобразование к цепочке только два раза. Реально мы можем позволить себе применение wavelet - преобразования 4-6 раз. Более того, дополнительное сжатие можно получить, используя таблицы алгоритма Хаффмана с неравномерным шагом (т.е. нам придется сохранять код Хаффмана для ближайшего в таблице значения). Эти приемы позволяют достичь заметных степеней сжатия.
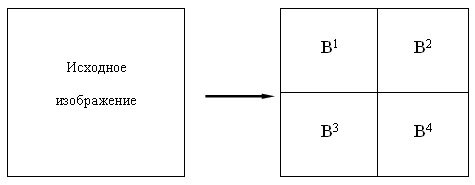
Алгоритм для двумерных данных реализуется аналогично. Если у нас есть квадрат из 4 точек с яркостями  то
то

(см. рис. 7.1)
Используя эти формулы, мы для изображения 512х512 пикселов получим после первого преобразования 4 матрицы размером 256х256 элементов: (рис. 7.2)
В первой, как легко догадаться, будет храниться уменьшенная копия изображения. Во второй - усредненные разности пар значений пикселов по горизонтали. В третьей - усредненные разности пар значений пикселов по вертикали. В четвертой - усредненные разности значений пикселов по диагонали. По аналогии с двумерным случаем мы можем повторить наше преобразование и получить вместо первой матрицы 4 матрицы размером 128х128. Повторив наше преобразование в третий раз, мы получим в итоге: 4 матрицы 64х64, 3 матрицы 128х128 и 3 матрицы 256х256. На практике при записи в файл, значениями, получаемыми в последней строке 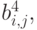 обычно пренебрегают (сразу получая выигрыш примерно на треть размера файла - 1- 1/4 - 1/16 - 1/64...).
обычно пренебрегают (сразу получая выигрыш примерно на треть размера файла - 1- 1/4 - 1/16 - 1/64...).
К достоинствам этого алгоритма можно отнести то, что он очень легко позволяет реализовать возможность постепенного "проявления" изображения при передаче изображения по сети. Кроме того, поскольку в начале изображения мы фактически храним его уменьшенную копию, упрощается показ "огрубленного" изображения по заголовку.
В отличие от JPEG и фрактального алгоритма данный метод не оперирует блоками, например, 8х8 пикселов. Точнее, мы оперируем блоками 2х2, 4х4, 8х8 и т.д. Однако за счет того, что коэффициенты для этих блоков мы сохраняем независимо, мы можем достаточно легко избежать дробления изображения на "мозаичные" квадраты.