Проблемы алгоритмов архивации с потерями

Построение алгоритма

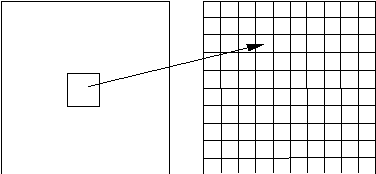
Как уже стало очевидным из изложенного выше, основной задачей при компрессии фрактальным алгоритмом является нахождение соответствующих аффинных преобразований. В самом общем случае мы можем переводить любые по размеру и форме области изображения, однако в этом случае получается астрономическое число перебираемых вариантов разных фрагментов, которое невозможно обработать на текущий момент даже на суперкомпьютере.

В учебном варианте алгоритма рис. 6.7, изложенном далее, сделаны следующие ограничения на области:

1. Все области являются квадратами со сторонами, параллельными сторонам изображения. Это ограничение достаточно жесткое. Фактически мы собираемся аппроксимировать все многообразие геометрических фигур лишь квадратами.
2. При переводе доменной области в ранговую уменьшение размеров производится ровно в два раза. Это существенно упрощает как компрессор, так и декомпрессор, т.к. задача масштабирования небольших областей является нетривиальной.
3. Все доменные блоки - квадраты и имеют фиксированный размер. Изображение равномерной сеткой разбивается на набор доменных блоков.
4. Доменные области берутся "через точку" и по Х, и по Y, что сразу уменьшает перебор в 4 раза.
5. При переводе доменной области в ранговую поворот куба возможен только на 0, 90, 180 градусов или 270 градусов. Также допускается зеркальное отражение. Общее число возможных преобразований (считая пустое) - 8.
6. Масштабирование (сжатие) по вертикали (яркости) осуществляется в фиксированное число раз - в 0,75.

Рис. 6.7.

Эти ограничения позволяют:

1. Построить алгоритм, для которого требуется сравнительно малое число операций даже на достаточно больших изображениях.
2. Очень компактно представить данные для записи в файл. Нам требуется на каждое аффинное преобразование в IFS:

• два числа для того, чтобы задать смещение доменного блока. Если мы ограничим входные изображения размером 512х512, то достаточно будет по 8 бит на каждое число.
• три бита для того, чтобы задать преобразование симметрии при переводе доменного блока в ранговый.
• 7-9 бит для того, чтобы задать сдвиг по яркости при переводе.

Информацию о размере блоков можно хранить в заголовке файла. Таким образом, мы затратили менее 4 байт на одно аффинное преобразование. В зависимости от того, каков размер блока, можно высчитать, сколько блоков будет в изображении. Таким образом, мы можем получить оценку степени компрессии.

Например, для файла в градациях серого 256 цветов 512х512 пикселов при размере блока 8 пикселов аффинных преобразований будет 4096 (512/8 512/8). На каждое потребуется 3.5 байта. Следовательно, если исходный файл занимал 262144 (512 512) байт (без учета заголовка), то файл с коэффициентами будет занимать 14336 байт. Степень сжатия - 18 раз. При этом мы не учитываем, что файл с коэффициентами тоже может обладать избыточностью и архивироваться методом архивации без потерь, например LZW.

Отрицательные стороны предложенных ограничений:

1. Поскольку все области являются квадратами, невозможно воспользоваться подобием объектов, по форме далеких от квадратов (которые встречаются в реальных изображениях достаточно часто.)
2. Аналогично мы не сможем воспользоваться подобием объектов в изображении, коэффициент подобия между которыми сильно отличается от 2.
3. Алгоритм не сможет воспользоваться подобием объектов в изображении, угол между которыми не кратен 900.

Такова плата за скорость компрессии и за простоту упаковки коэффициентов в файл.

Сам алгоритм упаковки сводится к перебору всех доменных блоков и подбору для каждого соответствующего ему рангового блока. Ниже приводится схема этого алгоритма.

for (all range blocks) {
    min_distance = MaximumDistance;
    Rij = image->CopyBlock(i,j);
    for (all domain blocks) { // С поворотами и отр.
      current=Координаты тек. преобразования;
      D=image->CopyBlock(current);
      current_distance = Rij.L2distance(D);
      if(current_distance < min_distance) {
        // Если коэффициенты best хуже: 
        min_distance = current_distance;
        best = current;
      }
    } // Next range block
    Save_Coefficients_to_file(best);
  } // Next domain block

Как видно из приведенного алгоритма, для каждого рангового блока делаем его проверку со всеми возможными доменными блоками (в том числе с прошедшими преобразование симметрии), находим вариант с наименьшей мерой 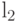(наименьшим среднеквадратичным отклонением) и сохраняем коэффициенты этого преобразования в файл. Коэффициенты - это (1) координаты найденного блока, (2) число от 0 до 7, характеризующее преобразование симметрии (поворот, отражение блока), и (3) сдвиг по яркости для этой пары блоков. Сдвиг по яркости вычисляется как:

где 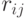- значения пикселов рангового блока (R), а 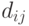- значения пикселов доменного блока (D). При этом мера считается как:

Мы не вычисляем квадратного корня из 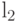меры и не делим ее на n, поскольку данные преобразования монотонны и не помешают нам найти экстремум, однако мы сможем выполнять на две операции меньше для каждого блока.

Посчитаем количество операций, необходимых нам для сжатия изображения в градациях серого 256 цветов 512х512 пикселов при размере блока 8 пикселов (табл. 6.1):

Таким образом, нам удалось уменьшить число операций алгоритма компрессии до вполне вычисляемых (пусть и за несколько часов) величин.