Проблемы алгоритмов архивации с потерями

Схема алгоритма декомпрессии изображений

Декомпрессия алгоритма фрактального сжатия чрезвычайно проста. Необходимо провести несколько итераций трехмерных аффинных преобразований, коэффициенты которых были получены на этапе компрессии.

В качестве начального может быть взято абсолютно любое изображение (например, абсолютно черное), поскольку соответствующий математический аппарат гарантирует нам сходимость последовательности изображений, получаемых в ходе итераций IFS, к неподвижному изображению (близкому к исходному). Обычно для этого достаточно 16 итераций.

Прочитаем из файла коэффициенты всех блоков;
  Создадим черное изображение нужного размера;
  Until(изображение не станет неподвижным){
    For(every range (R)){
      D=image->CopyBlock(D_coord_for_R);
      For(every pixel(i,j) in the block{
        Rij = 0.75Dij + oR; 
      } //Next pixel
    } //Next block
  }//Until end

Поскольку мы записывали коэффициенты для блоков 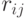(которые, как мы оговорили, в нашем частном случае являются квадратами одинакового размера) последовательно, то получается, что мы последовательно заполняем изображение по квадратам сетки разбиения использованием аффинного преобразования.

Как можно подсчитать, количество операций на один пиксел изображения в градациях серого при восстановлении необычайно мало ( N операций сложения "+" и N операций умножения "*", где N - количество итераций, т.е. 7-16). Благодаря этому, декомпрессия изображений для фрактального алгоритма проходит быстрее декомпрессии, например, для алгоритма JPEG. В простой реализации JPEG на точку приходится 64 операции сложения "+" и 64 операции умножения "*". При реализации быстрого ДКП можно получить, 7 сложений и 5 умножений на точку, но это без учета шагов RLE, квантования и кодирования по Хаффману. При этом для фрактального алгоритма умножение происходит на рациональное число, одно для каждого блока. Это означает, что мы можем, во-первых, использовать целочисленную рациональную арифметику, которая быстрее арифметики с плавающей точкой. Во-вторых, можно использовать умножение вектора на число - более простую и быструю операцию, часто закладываемую в архитектуру процессора (процессоры SGI, Intel MMX, векторные операции Athlon и т.д.). Для полноцветного изображения ситуация качественно не изменяется, поскольку перевод в другое цветовое пространство используют оба алгоритма.

Оценка потерь и способы их регулирования

При кратком изложении упрощенного варианта алгоритма были пропущены многие важные вопросы. Например, что делать, если алгоритм не может подобрать для какого-либо фрагмента изображения подобный ему? Достаточно очевидное решение - разбить этот фрагмент на более мелкие, и попытаться поискать для них. В то же время понятно, что эту процедуру нельзя повторять до бесконечности, иначе количество необходимых преобразований станет так велико, что алгоритм перестанет быть алгоритмом компрессии. Следовательно, мы допускаем потери в какой-то части изображения.

Для фрактального алгоритма компрессии, как и для других алгоритмов сжатия с потерями, очень важны механизмы, с помощью которых можно будет регулировать степень сжатия и степень потерь. К настоящему времени разработан достаточно большой набор таких методов. Во-первых, можно ограничить количество аффинных преобразований, заведомо обеспечив степень сжатия не ниже фиксированной величины. Во-вторых, можно потребовать, чтобы в ситуации, когда разница между обрабатываемым фрагментом и наилучшим его приближением будет выше определенного порогового значения, этот фрагмент дробился обязательно (для него обязательно заводится несколько "линз"). В-третьих, можно запретить дробить фрагменты размером меньше, допустим, четырех точек. Изменяя пороговые значения и приоритет этих условий, мы будем очень гибко управлять коэффициентом компрессии изображения в диапазоне от побитового соответствия до любой степени сжатия. Заметим, что эта гибкость будет гораздо выше, чем у ближайшего "конкурента" - алгоритма JPEG.