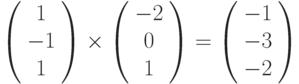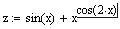Основные средства программы MathCAD
1.4. Ввод и вычисление математических выражений
Конструирование выражений в MathCAD осуществляется с помощью математических панелей. Ввод заканчивается клавишей Enter или щелчком мыши вне определения. Синий уголок показывает текущий операнд выражения, он может быть расширен клавишей "Пробел". В качестве разделителя целой и дробной части числа используется точка.
Арифметические операции, простейшие функции, знаки присваивания переменным (символ :=) можно вводить, используя панель Calculator (Калькулятор). Численные ответы выражений определяются нажатием клавиши [=] на клавиатуре. В качестве элементов выражения могут использоваться функции определенных интегралов, сумм и произведений с панели Calculus.
Для ввода математической функции различной категории используется команда Insert /Function (Вставить функцию).
Для ввода текстового комментария необходимо ввести знак двойной кавычки ", затем вводить текст. Текстовая область, как и любая другая, может быть перемещена на рабочем листе или скопирована в буфер. Маркеры текстовой области позволяют менять её размеры
1.4.1. Переменные и функции.
Переменная в MathCAD – это идентификатор, который используется в выражениях и которому можно присвоить числовое значение. Идентификатор – набор букв и цифр, первым из которых должна быть буква; буквы могут быть латинскими или греческими с соответствующей панели; малые и большие буквы различаются; в качестве цифры может использоваться символ подчеркивания. При выполнении цепочки выражений последовательность вычислений в документе определяется слева - направо и сверху - вниз. Чтобы цепочка выражений была вычислена, надо всем переменным присвоить числовые значения. Присваивания бывают двух видов: локальные и глобальные. Локальное присваивание осуществляется нажатием символа := на панели Калькулятор. Присвоенное значение в документе начинает действовать с момента его записи (слева-напрво и сверху-вниз).
Глобальное присваивание действует в пределах всего документа независимо от места его определения. Глобальное присваивание определяется символом === с панели Evaluation. Ниже (Рис.1.10) приведен пример цепочки выражений с использованием локального (для х) и глобального (для а) присваивания:

 ,
,  ,
, 
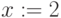 ,
, 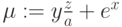
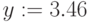 ,
, 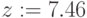 ,
, 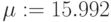
Встроенные константы
Символьный процессор распознает и способен выдавать математические константы в качестве результата.
Вычислительный процессор воспринимает как числа
 -бесконечность ( клавиши <Ctrl>+<Shift>+<z>);
-бесконечность ( клавиши <Ctrl>+<Shift>+<z>);
 - основание натурального логарифма (клавиша <е>);
- основание натурального логарифма (клавиша <е>);
 ; - число "пи" (вводится клавишами <Ctrl>+<Shift>+<p>);
; - число "пи" (вводится клавишами <Ctrl>+<Shift>+<p>);
 - мнимая единица (вводится клавишами <1>, <i> или <1>, <j>);
- мнимая единица (вводится клавишами <1>, <i> или <1>, <j>);
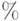 - символ процента, <%>, эквивалентный 0,01.
- символ процента, <%>, эквивалентный 0,01.
Основные типы переменных
Действительные числа
Любое выражение, начинающееся с цифры, MathCAD интерпретирует как число. Числа набираются на клавиатуры в нужном формате (Рис.1.11). Форматы представлены в окне Format/Result (Рис.1.7.).
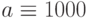
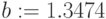
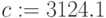
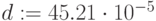
Комплексные числа
Комплексное число является суммой действительного и мнимого числа, получающегося путем умножения любого действительного числа на мнимую единицу (imaginary unit) i. По определению полагается, i2=-1. Для ввода мнимой единицы надо нажать клавиши <1>, <i.> (Рис.1.12). Если просто ввести символ "i", то MathCAD интерпретирует его как переменную i.
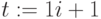

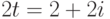
Размерные значения
В MathCAD числовые переменные и функции могут обладать размерностью. Используется команда Insert / Unit (Вставка / Единицы). "Горячая" клавиша <Ctrl>+<U>. В программе встроено большое количество единиц измерения, с помощью которых и создаются размерные переменные. Для ввода размерного значения - сразу после ввода переменной ввести символ умножения, в окне Insert / Unit списке Unit (Единицы) выбрать нужную единицу измерения
Pедактирование формул
В программе MathCAD при вводе формул курсор имеет вид: синего уголка ("клюшка") . Действие производится только с объектом, выделенным этим уголком. Для того чтобы охватить синим уголком блок, надо нажать на пробел один или несколько раз.
- Набираемая формула всегда заключена в рамку. Не выходите из рамки, пока не закончили набор формулы!
- Для набора формул пользуйтесь "Калькулятором" из "Математической палитры"
При наборе формул возможно появление ошибок набора. Кнопка  на стандартной панели инструментов позволяет отменить последнее действие, выполненное при редактировании, т.е. вернуться к тексту, набранному ранее.
на стандартной панели инструментов позволяет отменить последнее действие, выполненное при редактировании, т.е. вернуться к тексту, набранному ранее.
Встроенные функции MathCAD
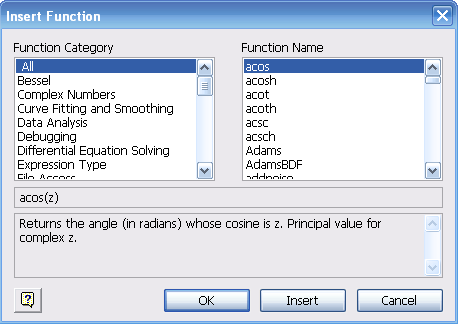
Стандартные математические функции и численные методы, запрограммированные в MathCAD, реализованы в виде встроенных функций. Для вставки функции команда меню Insert /Function (Вставить функцию)(Рис.1.17).
Собственные функции пользователя
Помимо широкого набора стандартных функций в MathCAD возможно определение собственных функций пользователя (Рис.1.14). В простейшем случае функция может быть определена выражением пользователя. Функция определяется следующим образом:
имя_функции(аргументы):=выражение,
где имя_функции – любой идентификатор; аргументы – список аргументов функции через запятую; выражение – любое выражение с использованием стандартных функций и функций пользователя, определенных в документе перед этим. Выражение должно содержать идентификаторы аргументов. Пример цепочки выражений с использованием функций пользователя приведен ниже:
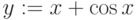
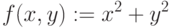
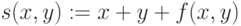

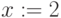

1.4.2. Массивы
Массивами (arrays) называют упорядоченные последовательности чисел или элементов. Доступ к любому элементу массива возможен по его индексу, т. е. номеру в последовательности чисел В MathCAD условно выделяются два типа массивов: векторы (одноиндексные массивы), матрицы (двухиндексные массивы), и тензоры (многоиндексные массивы); ранжированные переменные (range variables) - векторы, элементы которых определенным образом зависят от их индекса.
Векторы и матрицы
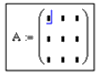
Матрицей размером mxn называется совокупность m•n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m x n записывают так
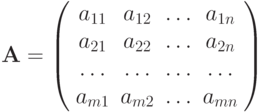
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы имеют два индекса aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце. Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. Матрицу с одним столбцом называют вектор-столбец, с одной строкой - вектор-строка.
Сложение матриц производится поэлементно, но размеры матриц должны совпадать Умножение матриц. осуществляется по своеобразному закону. Прежде всего, размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
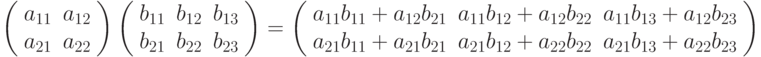
Например, в произведении - матрице C, элемент стоящий в 1-ой строке и 1-м столбце c11, равен сумме произведений элементов 1-ой строки матрицы A и 1 столбца матрицы B,
Создаются матрицы при помощи кнопки  палитры инструментов Matrix или команды Insert/Matrix (Рис.1.18, Рис.1.19, Рис.1.20). Появляется окно Insert matrix, где указывается количество строк, столбцов Rows и Columns.
палитры инструментов Matrix или команды Insert/Matrix (Рис.1.18, Рис.1.19, Рис.1.20). Появляется окно Insert matrix, где указывается количество строк, столбцов Rows и Columns.
Действия с матрицами производятся с помощью кнопок палитры Matrix .
-
сложение матриц
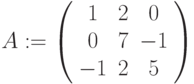 ,
, 

-
умножение матриц
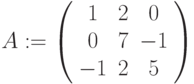 ,
, 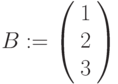
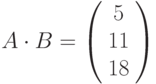

-
вычисление определителя матрицы, кнопка
 (Ctrl)
(Ctrl)
-
вычисление обратной матрицы
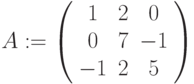 ,
, 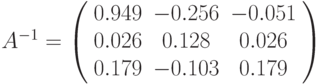
-
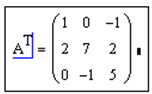
транспонирование матрицы
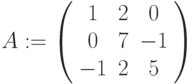 ,
, 
-
скалярное произведение (кнопка
 )
)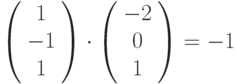
-
векторное произведение (кнопка
 )
)