|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Начало работы с библиотекой OpenCV
1.4.2. Работа с матрицами
Как было сказано ранее, если хочется провести небольшой эксперимент с OpenCV, как правило Питон будет наилучшим выбором. К C++ же имеет смысл обращаться, когда хочется сделать свой алгоритм работающий непосредственно с пикселями изображений, и делающий это эффективно, или для реализации уже конечного приложения, не прототипа. В любом случае, как только вы начинаете использовать OpenCV из C++, вы немедленно столкнетесь с типом cv::Mat (матрица), который в OpenCV используется для хранения почти всех объектов – изображений, массивов точек, векторных полей вычисляемых алгоритмами оптического поток, обычных матриц и т.д. Собственно, это аналогично MATLAB, где почти все данные хранятся в массивах. Итак, класс cv::Mat реализует многомерные многоканальные массивы.
При его использовании вы освобождаете себя от забот по управлению памятью: выделению и освобождению. Класс реализует счетчик ссылок и память освобождается только тогда, когда она больше не нужна.
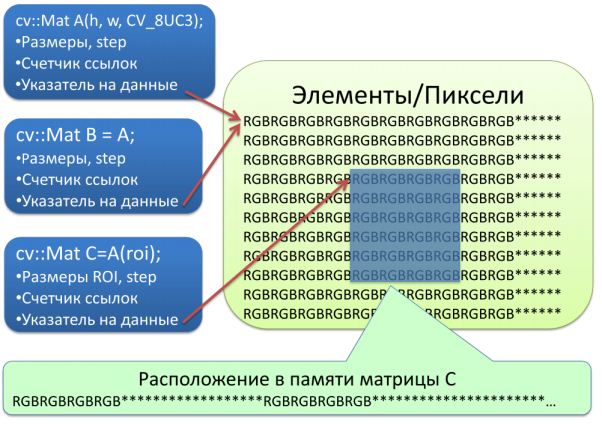
Изображение – это двумерный массив. Все его элементы расположены подряд по строкам. Кроме числа строк и числа столбцов имеется параметр step, равный расстоянию между строками. Этот параметр не меньше числа столбцов, но может быть его больше. В последнем случае в конце каждой строки имеется неиспользуемое пространство.
Предположим, вы создали некоторую матрицу (матрица A на рисунке выше), указав число ее строк и столбцов и опционально начальное значение для элементов матрицы. Параметр step вычисляется автоматически, выделяется буфер память нужного размера, при необходимости заполняется заданным значением. Счетчик ссылок приравнивается к 1. Если эта матрица присваивается другой матрице (матрица B на рисунке), то физического копирования данных не происходит, но на 1 увеличивается счетчик ссылок, а указатель данных указывает на то же место в памяти. Как только вы завершаете работу с каким либо объектом, счетчик ссылок уменьшается на 1. При достижении значения 0 память освобождается.
Допустим, вы нашли лицо на изображении и хотите найти на нем глаза. В этом случае вам нужно не все изображение, а только его часть, соответствующая лицу. Для этого удобно создать матрицу, являющуюся частью другой матрицы, при этом можно избежать копирования данных (матрица C на рисунке). Заметим, что параметр step для такой подматрицы будет равен параметру step исходной матрицы. Указатель на данные будет указывать на начало подматрицы. Счетчик ссылок после создания такой подматрицы также увеличивается на 1.
Если необходимо настоящее копирование данных, нужно использовать метод clone(), например:
cv::Mat M2 = M.clone();
Любому элементу матрицы можно присвоить значение. Делается это с помощью метода .at(y,x), где y – номер строки, x – номер столбца. Рассмотрим небольшой пример.
Mat M(480,640,CV_8UC1); // Создаем изображение 640x480 Rect roi(100, 200, 20, 20); // Определяем ROI Mat subM = M(roi); // Выделяем ROI в отдельную матрицу subM.at<uchar>(y,x)=255; // Изменяем пиксель (x,y) в subM и (x+100, y+200) в M
Так как в данном примере данные одни и те же, то изменяя подматрицу subM, вы изменяете и матрицу M. Продолжим этот пример и покажем, как работать с итераторами. Пусть в выбранном ROI необходимо оценить "резкость", определяемую как сумму модулей градиентов, вычисленных в каждом пикселе. Эта задача может быть полезной для реализации автофокуса (автофокус соответствует локальному максимуму функции "резкости"). Необходимо пробежаться по всем пикселам, найти в каждом из них градиент, вычислить его модуль и прибавить к сумматору. Для того чтобы пройтись по всем элементам матрицы, удобно использовать итераторы, похожие на итераторы из стандартной библиотеке stl:
Mat_<Vec3b>::iterator it= subM.begin<Vec3b>(),
itEnd = subM.end<Vec3b>();
float contrast = 0.f;
for(; it != itEnd; ++it)
{
uchar* ptr = &(*it);
int dx = ptr[1] – ptr[-1],
dy = ptr[subM.step] – ptr[-subM.step];
contrast += sqrtf((float)(dx*dx + dy*dy));
}
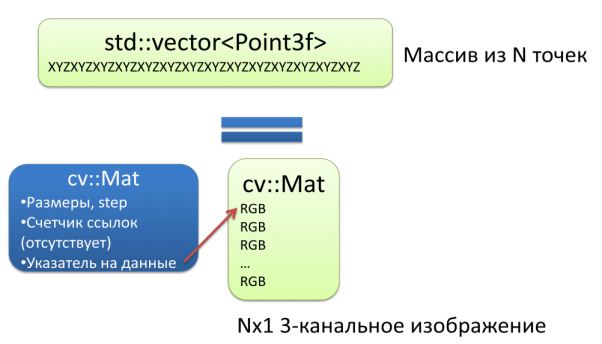
Кроме матриц библиотека OpenCV умеет работать с обычными STL векторами. При этом внутри библиотеки вектора часто обрабатываются как обычные матрицы (cv::Mat). То есть, для входного вектора внутри библиотеки дополнительно создается заголовок cv::Mat, который указывает на те же данные (данные не копируются). По завершении обработки временный заголовок удаляется.
1.4.3. Пример: поиск плоских объектов
В качестве практического примера использования OpenCV c С++ рассмотрим задачу поиска на изображении плоских объектов. Пусть имеется некоторое изображение плоского объекта, например, передняя грань коробки. Требуется найти этот объект на другом большом изображении некоторой сложной сцены. Коробка может быть загорожена другими объектами, ориентирована произвольным образом в пространстве. Освещение сцены может быть иным.
Основная идея метода – нахождение особых точек, т. е. точек, примечательных для данного объекта, за которые можно "зацепиться". Однородные участки поверхности для идентификации объекта обычно не подходят, так как могут совпасть с чем угодно. Если возьмем окрестность более интересных точек – то случайное совпадение маловероятно. Мы находим точки, строим их описание (дескрипторы), и пытаемся найти похожие точки на втором изображение. После чего отфильтровываем неправильно сопоставленные точки, исходя из гипотезы что объект жесткий (недеформируемый) и поэтому все точки на нем должны преобразовываться от одного кадра к другому согласованно. В случае плоского объекта это должно быть перспективное преобразование (гомография).
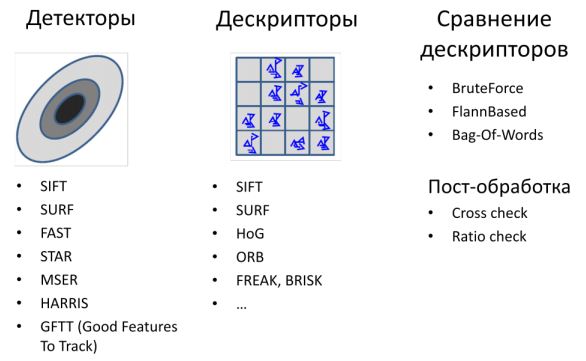
Все необходимое для реализации этого метода есть в модуле features2d. Он позволяет находить особые точки, строить их дескрипторы, применять методы сравнения дескрипторов.
Приведем код, решающий данную задачу:
// Загружаем изображения:
Mat img1 = imread(argv[1], CV_LOAD_IMAGE_GRAYSCALE);
Mat img2 = imread(argv[2], CV_LOAD_IMAGE_GRAYSCALE);
// Находим особые точки на каждом изображении
// Вычисляем их дескрипторы:
Ptr<Feature2D>
surf=Algorithm::create<Feature2D>("Feature2D.SURF");
vector<KeyPoint> keypoints1, keypoints2;
Mat descriptors1, descriptors2;
surf->operator()(img1, Mat(), keypoints1, descriptors1); surf->operator()(img2, Mat(), keypoints2, descriptors2);
// Находим наилучшее соответствие между особыми точками
// на изображениях
vector<DMatch> matches;
BFMatcher(NORM_L2, true).match(descriptors1, descriptors2,
matches);
// Находим оптимальное преобразование,
// согласующееся с большинством пар точек.
vector<Point2f> pt1, pt2;
for( size_t i = 0; i < matches.size(); i++ ) {
pt1.push_back(keypoints1[matches[i].queryIdx].pt);
pt2.push_back(keypoints2[matches[i].trainIdx].pt);
}
// H – это матрица оптимального перспективного
// преобразования от img1 к img2
Mat H = findHomography(pt1, pt2, RANSAC, 10);
Мы загружаем оба изображения. Находим особые точки и вычисляем их дескрипторы. При этом создаем экземпляр алгоритма Feature2D, используя параметры по умолчанию. В результате получаем 2 "списка" особых точек и 2 "списка" их дескрипторов: keypoints1, keypoints2, descriptors2, descriptors2, при этом keypoints1, keypoints2 – это векторы, содержащие номера особых точек, а descriptors2, descriptors2 – матрицы, строки которых содержат их дескрипторы. На рисунке указаны найденные особые точки.
После этого, сравнивая каждый набор дескрипторов из первого изображения, с каждым таким набором из второго изображения, находим наилучшее соответствие между особыми точками.
На рисунке графически изображено найденное соответствие.
Далее находим матрицу наилучшего перспективного преобразования (гомографии), осуществляющую это соответствие.
На рисунке отмечены "правильные" пары особых точек, т. е. пары, подчиняющиеся найденному перспективному преобразованию. Обратите внимание на пару точек (самый верхний отрезок), найденную ошибочно (эти точки принадлежат разным объектам), но геометрически не противоречащую остальным парам.
После того как матрица гомографии найдена само расположение коробки в пространтсве можно найти с помощью функции solvePnP().
Заметим, что данный метод работает также для склейки панорам, если снимаемая сцена (например пейзаж) находится достаточно далеко от точки съемки, чтобы считать ее плоской.
В случае неплоских объектов, "правильные" пары можно найти с помощью findFundamentalMat() вместо findHomography(), после чего опять использовать solvePnP().





 "
"