|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
Детекторы и дескрипторы ключевых точек. Алгоритмы классификации изображений. Задача детектирования объектов на изображениях и методы её решения
2. Обзор дескрипторов ключевых точек
Результатом работы детекторов является множество особых точек, для которых необходимо построить математическое описание. В настоящем разделе делается обзор некоторых существующих дескрипторов.
Входными данными дескриптора является изображение и набор особых точек, выделенных на заданном изображении. Выходом дескриптора является множество векторов признаков для исходного набора особых точек. Необходимо отметить, что какие-то дескрипторы решают одновременно две задачи – поиск особых точек и построение описателей этих точек.
Признаки (описатели) строятся на основании информации об интенсивности, цвете и текстуре особой точки. Но особые точки могут представляться углами, ребрами или даже контуром объекта, поэтому, как правило, вычисления выполняются для некоторой окрестности. В идеале хорошие признаки должны обладать рядом свойств:
- Повторямость. На изображениях одного и того же объекта или сцены, сделанных с разных точек зрения и при разных условиях освещенности, большинство признаков должно быть продетектировано.
- Локальность. Признаки должны быть максимально локальными, чтобы снизить вероятность перекрытий.
- Репрезентативность. Количество признаков должно быть достаточным, чтобы разумное число признаков детектировалось даже на небольшом изображении объекта.
- Точность. Признаки должны быть точно продетектированными по отношению к масштабу и форме объекта.
- Эффективность. Для приложений реального времени критично, чтобы процедура вычисления признаков не требовала значительных вычислительных затрат.
2.1. Дескриптор SIFT
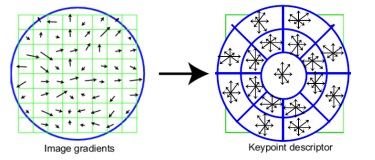
Для формирования дескриптора SIFT (Scale Invariant Feature Transform) [ 105 , 73 , 109 ] сначала вычисляются значения магнитуды и ориентации градиента в каждом пикселе, принадлежащем окрестности особой точки размером  пикселей. Магнитуды градиентов при этом учитываются с весами, пропорциональными значению функции плотности нормального распределения с математическим ожиданием в рассматриваемой особой точке и стандартным отклонением, равным половине ширины окрестности (веса Гауссова распределения используются для того, чтобы уменьшить влияние на итоговый дескриптор градиентов, вычисленных в пикселях, находящихся дальше от особой точки).
пикселей. Магнитуды градиентов при этом учитываются с весами, пропорциональными значению функции плотности нормального распределения с математическим ожиданием в рассматриваемой особой точке и стандартным отклонением, равным половине ширины окрестности (веса Гауссова распределения используются для того, чтобы уменьшить влияние на итоговый дескриптор градиентов, вычисленных в пикселях, находящихся дальше от особой точки).
В каждом квадрате размером  пикселя вычисляется гистограмма ориентированных градиентов путем добавления взвешенного значения магнитуды градиента к одному из 8 бинов гистограммы. Чтобы уменьшить различные "граничные" эффекты, связанные с отнесением похожих градиентов к разным квадратам (что может возникнуть вследствие небольшого сдвига расположения особой точки) используется билинейная интерполяция: значение магнитуды каждого градиента добавляется не только в гистограмму, соответствующую квадрату, к которому данный пиксель относится, но и к гистограммам, соответствующим соседним квадратам. При этом значение магнитуды добавляется с весом, пропорциональным расстоянию от пикселя, в котором вычислен данный градиент, до центра соответствующего квадрата. Все вычисленные гистограммы объединяются в один вектор, размером, равным
пикселя вычисляется гистограмма ориентированных градиентов путем добавления взвешенного значения магнитуды градиента к одному из 8 бинов гистограммы. Чтобы уменьшить различные "граничные" эффекты, связанные с отнесением похожих градиентов к разным квадратам (что может возникнуть вследствие небольшого сдвига расположения особой точки) используется билинейная интерполяция: значение магнитуды каждого градиента добавляется не только в гистограмму, соответствующую квадрату, к которому данный пиксель относится, но и к гистограммам, соответствующим соседним квадратам. При этом значение магнитуды добавляется с весом, пропорциональным расстоянию от пикселя, в котором вычислен данный градиент, до центра соответствующего квадрата. Все вычисленные гистограммы объединяются в один вектор, размером, равным  (число бинов)
(число бинов) 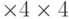 (число квадратов).
(число квадратов).
Полученный дескриптор преобразуется, чтобы уменьшить возможные эффекты от изменения освещенности. Изменение контраста изображения (значение интенсивности каждого пикселя умножается на некоторую константу) приводит к такому же изменению в значениях магнитуд градиентов. Поэтому очевидно, что данный эффект может быть нивелирован путем нормализации дескриптора таким образом, чтобы его длина стала равна единице. Изменения яркости изображения (к значению интенсивности каждого пикселя прибавляется некоторая константа) не влияют на значения магнитуд градиентов. Таким образом, SIFT-дескриптор является инвариантным по отношению к аффинным изменениям освещенности. Однако могут возникать и нелинейные изменения в освещенности вследствие, например, различной ориентации источника света по отношению к поверхностям трехмерного объекта. Данные эффекты могут вызвать большое изменение в отношении магнитуд некоторых градиентов (при этом оказывают незначительное влияние на ориентацию вектора градиента). Чтобы избежать этого, используют отсечение по некоторому порогу (по результатам экспериментов показано, что оптимальным является значение 0.2), которое применяют к компонентам нормализованного дескриптора. После применения порога дескриптор вновь нормализуется. Таким образом, уменьшается значение больших магнитуд градиентов и увеличивается значение распределения ориентаций данных градиентов в окрестности особой точки.
2.2. Дескриптор PCA-SIFT
Дескриптор PCA-SIFT [ 105 , 64 ] по существу является модификацией SIFT. На начальном этапе аналогично вычисляются значения магнитуды и ориентации градиента. Только для каждой особой точки рассматривается окрестность размером  пиксель с центром в точке, которая является особой. По факту строится карта градиентов вдоль вертикального и горизонтального направлений. Как следствие, получается вектор, содержащий
пиксель с центром в точке, которая является особой. По факту строится карта градиентов вдоль вертикального и горизонтального направлений. Как следствие, получается вектор, содержащий 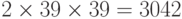 элементов. Далее выполняется построение SIFT дескриптора согласно схеме, описанной в предыдущем разделе. Для результирующего набора SIFT дескрипторов осуществляется снижение размерности векторов до 32 элементов посредством анализа главных компонент (Principal Component Analysis, PCA).
элементов. Далее выполняется построение SIFT дескриптора согласно схеме, описанной в предыдущем разделе. Для результирующего набора SIFT дескрипторов осуществляется снижение размерности векторов до 32 элементов посредством анализа главных компонент (Principal Component Analysis, PCA).
2.3. Дескриптор SURF
Дескриптор SURF (Speeded up Robust Features) [ 14 , 109 ] относится к числу тех дескрипторов, которые одновременно выполняют поиск особых точек и строят их описание, инвариантное к изменению масштаба и вращения. Кроме того, сам поиск ключевых точек обладает инвариантностью в том смысле, что повернутый объект сцены имеет тот же набор особых точек, что и образец.
Определение особых точек на изображении выполняется на основании матрицы Гессе (FAST-Hessian detector, [ 109 ]). Использование Гессиана обеспечивает инвариантность относительно преобразования типа "поворот", но не инвариантность относительно изменения масштаба. Поэтому SURF применяет фильтры разного масштаба для вычисления Гессиана. Предположим, что исходное изображение задается матрицей интенсивностей  , текущий рассматриваемый пиксель обозначим через
, текущий рассматриваемый пиксель обозначим через 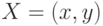 , а
, а  – масштаб фильтра. Тогда матрица Гессе имеет вид:
– масштаб фильтра. Тогда матрица Гессе имеет вид:
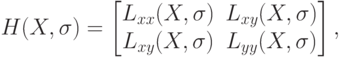
где 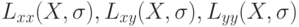 – свертки аппроксимации второй производной Гауссова ядра с изображением
– свертки аппроксимации второй производной Гауссова ядра с изображением  . Детерминант матрицы Гессе достигает экстремума в точках максимального изменения градиента яркости. Поэтому SURF пробегается фильтром с Гауссовым ядром по всему изображению и находит точки, в которых достигается максимальное значение детерминанта матрицы Гессе. Отметим, что такой проход выделяет как темные пятна на белом фоне, так и светлые пятна на темном фоне.
. Детерминант матрицы Гессе достигает экстремума в точках максимального изменения градиента яркости. Поэтому SURF пробегается фильтром с Гауссовым ядром по всему изображению и находит точки, в которых достигается максимальное значение детерминанта матрицы Гессе. Отметим, что такой проход выделяет как темные пятна на белом фоне, так и светлые пятна на темном фоне.
Далее для каждой найденной особой точки вычисляется ориентация – преобладающее направление перепада яркости. Понятие ориентации близко к понятию направления градиента, но для определения ориентации особой точки применяется фильтр Хаара [ 114 ].
На основании имеющейся информации выполняется построение дескрипторов для каждой особой точки:
- Вокруг точки строится квадратная окрестность размером
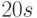 , где
, где  – масштаб, на котором получено максимальное значение детерминанта матрицы Гесса.
– масштаб, на котором получено максимальное значение детерминанта матрицы Гесса. - Полученная квадратная область разбивается на блоки, в результате область будет разбита на
 региона.
региона. - Для каждого блока вычисляются более простые признаки. Как следствие, получается вектор, содержащий 4 компоненты: 2 – это суммарный градиент по квадранту, 2 – сумма модулей точечных градиентов.
- Дескриптор формируется в результате склеивания взвешенных описаний градиента для 16 квадрантов вокруг особой точки. Элементы дескриптора взвешиваются на коэффициенты Гауссова ядра. Веса необходимы для большей устойчивости к шумам в удаленных точках.
- Дополнительно к дескриптору заносится след матрицы Гессе. Эти компоненты необходимы, чтобы различать темные и светлые пятна. Для светлых точек на темном фоне след отрицателен, для темных точек на светлом фоне – положителен.
Отметим, что SURF используется для поиска объектов. Тем не менее, дескриптор никак не использует информацию об объектах. SURF рассматривает изображение как единое целое и выделяет особенности всего изображения, поэтому он плохо работает с объектами простой формы.
2.4. Дескриптор GLOH
Дескриптор GLOH (Gradient location-orientation histogram) [ 77 ] является модификацией SIFT-дескриптора, который построен с целью повышения надежности. По факту вычисляется SIFT дескриптор, но используется полярная сетка разбиения окрестности на бины (рис. 3.2): 3 радиальных блока с радиусами 6, 11 и 15 пикселей и 8 секторов. В результате получается вектор, содержащий 272 компоненты, который проецируется в пространство размерности 128 посредством использования анализа главных компонент (PCA).
2.5. Дескриптор DAISY
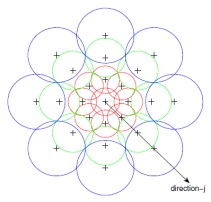
Детектор DAISY [ 107 ] изначально вводится для решения задачи сопоставления изображений (matching) в случае значительных внешних изменений, т.е. данный дескриптор в отличие от ранее рассмотренных работает на плотном множестве пикселей всего изображения. При этом авторы DAISY в работе [ 107 ] показали, что дескриптор работает в 66 раз быстрее, чем SIFT, запущенный на плотном множестве пикселей. В DAISY использованы идеи построения SIFT и GLOH дескрипторов. Аналогично GLOH выбирается круговая окрестность особой точки, при этом бины представляются не частичными секторами, а окружностями (рис. 3.3).
Для каждого такого бина выполняется та же последовательность действий, что и в алгоритме SIFT, но взвешенная сумма магнитуд градиентов заменяется сверткой исходного изображения с производными Гауссова фильтра, взятыми по 8 направлениям. Авторы [ 107 ] показали, что построенный дескриптор обладает инвариантностью, как и SIFT, и GLOH, при этом для решения задачи сопоставления (matching) в случае, когда все пиксели считаются особыми, требует меньших вычислительных затрат.
2.6. Дескриптор BRIEF
Цель создания BRIEF-дескриптора (Binary Robust Independent Elementary Features) [ 22 ] состояла в том, чтобы обеспечить распознавание одинаковых участков изображения, которые были сняты с разных точек зрения. При этом ставилась задача максимально уменьшить количество выполняемых вычислений. Алгоритм распознавания сводится к построению случайного леса (randomize classification trees) или наивного Байесовского классификатора на некотором тренировочном множестве изображений и последующей классификации участков тестовых изображений. В упрощенном варианте может использоваться метод ближайшего соседа для поиска наиболее похожего патча в тренировочной выборке. Небольшое количество операций обеспечивается за счет представления вектора признаков в виде бинарной строки, а как следствие, использования в качестве меры сходства расстоянии Хэмминга.
Схема построения векторов признаков достаточно простая. Изображение разбивается на патчи (отдельные перекрывающиеся участки). Допустим патч  имеет размеры
имеет размеры  пикселей. Из патча выбирается некоторым образом множество пар пикселей
пикселей. Из патча выбирается некоторым образом множество пар пикселей  для которых строится набор бинарных тестов:
для которых строится набор бинарных тестов:

где 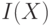 – интенсивность пикселя
– интенсивность пикселя  . Для каждого патча выбирается множество, содержащее
. Для каждого патча выбирается множество, содержащее  пар точек, которые однозначно определяют набор бинарных тестов. Далее на основании этих тестов строится бинарная строка:
пар точек, которые однозначно определяют набор бинарных тестов. Далее на основании этих тестов строится бинарная строка:

Авторы [ 22 ] приводят результаты экспериментов (качества распознавания) при выборе пар точек согласно закону равномерного распределения в патче, а также нормального распределения с разными значениями математического ожидания и среднеквадратичного отклонения. Отметим, что при одинаковых условиях проведения экспериментов на некоторых тестовых изображениях точность детектирования с помощью BRIEF почти в 1.5 раза выше, чем с использованием SURF-дескрипторов.