Параллельные алгоритмы

Вычисление определенного интеграла

Задача вычисления определенного интеграла

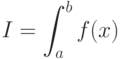( 3.11)

встречается в самых разных приложениях. Численные методы позволяют вычислить интеграл с заданной точностью, сводя вычисление интеграла к суммированию:

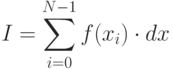( 3.12)

Геометрически значение интеграла задает площадь фигуры, образованной графиком подынтегральной функции f(x). Простейший численный метод - метод прямоугольников - вычисляет значение интеграла, как сумму площадей N прямоугольников, у которых основание равно dx, а высота равна значению подынтегральной функции в точке . При выбранном значении N значение dx и координата вычисляются по следующим формулам:

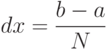( 3.13)

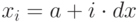
Если выбрать N достаточно большим, то формула (3.12) дает хорошую аппроксимацию значения интеграла. Рис. 3.1 иллюстрирует сущность метода прямоугольников.

Рис. 3.1. Метод прямоугольников численного вычисления интеграла

На рисунке N равно двум и приближенное значение интеграла равно сумме площадей двух выделенных прямоугольников. Конечно же, при таком малом N трудно ожидать хорошей аппроксимации. Значение N следует существенно увеличить. Но как велико должно быть N? Это зависит как от величины интервала интегрирования, так и от поведения функции. Для осциллирующих функций N может быть очень велико.

Численный метод интегрирования предполагает итерирование по N. Это означает построение цикла, на каждой итерации которого значение N увеличивается (обычно в два раза). Если значения вычисленных сумм на соседних итерациях по модулю отличаются на величину меньшую заданной точности, то итерирование прекращается.

Метод прямоугольников хорош тем, что нетрудно написать реализацию, в которой на каждом шаге цикла по N значения функции рассчитываются только в новых точках. Сумма, вычисленная на предыдущей итерации, используется для вычисления нового значения.

Последовательный алгоритм в этом случае имеет временную сложность, заданную соотношением:

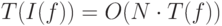( 3.14)

Здесь N - это то конечное значение, при котором достигается требуемая точность. Цикл итерирования по N не вносит дополнительной сложности вычисления.

Давайте построим реализацию этого алгоритма. Первым делом зададим класс, описывающий подынтегральные функции:

public delegate double Integral_function(double x);

Все функции этого класса принимают один аргумент типа double и возвращают значение такого же типа.

Построим теперь класс NewIntegral, содержащий различные методы вычисления интеграла. Вот как выглядит общая часть этого класса, содержащая описание полей класса, методов свойств и конструктора объектов:

/// <summary>
    /// Вычисление определенного интеграла 
    /// разными методами
    /// </summary>
    public class NewIntegral
    {
        double a, b;    //пределы интегрирования
        Integral_function f;    //подынтегральная функция
        int p;          //число сегментов разбиения 
        double eps;     //точность вычисления
        double result;  //результат вычисления
        object locker = new object();
        double[] results;
        public double Result
        {
            get { return result; }
        }
        /// <summary>
        /// конструктор 
        /// </summary>
        /// <param name="a">нижний предел интегрирования</param>
        /// <param name="b">верхний предел интегрирования</param>
        /// <param name="p">число сегментов разбиения интервала
                                     интегрирования</param>
        /// <param name="f">подынтегральная функция</param>
        /// <param name="eps">точность вычисления интеграла</param>
        public NewIntegral(double a, double b, int p,
            Integral_function f, double eps)
        {
            this.a = a;
            this.b = b;
            this.p = p;
            this.f = f;
            this.eps = eps;
            results = new double[p];
        }

Добавим теперь в наш класс метод, реализующий последовательное вычисление интеграла по рассмотренной выше схеме прямоугольников:

/// <summary>
        /// Последовательный алгоритм
        /// </summary>
        /// <param name="a">начало отрезка интегрирования</param>
        /// <param name="b">конец отрезка интегрирования</param>
        void DefiniteIntegral(double a, double b, out double result)
        {
            int n = 2;
            double dx = (b - a) / 2;
            double S0 = 0, S = 0;
            double x = 0;
            bool success = false;
            for (int i = 0; i < n; i++)
            {
                x = a + i * dx;
                S0 += f(x);
            }
            S0 *= dx;
            while (!success)
            {
                n = 2 * n;
                dx = dx / 2;
                S = 0;
                for (int i = 1; i < n; i += 2)
                {
                    x = a + i * dx;
                    S += f(x);
                }
                S = S * dx + S0 / 2;
                if (Math.Abs(S - S0) > eps)
                    S0 = S;
                else
                    success = true;
            }
            result = S;
        }

Простой и эффективный алгоритм 3.9 полностью реализует описанную выше идею. Вначале вычисляется сумма при n, равном 2. Затем в цикле по while осуществляется итерирование по n. На каждой итерации используется ранее посчитанная сумма, к которой добавляются слагаемые, построенные для новых точек разбиения отрезка интегрирования.

Заметьте, подынтегральная функция f задана как поле класса.

Алгоритм 3.9 прост и эффективен для последовательного выполнения, но требует модификации для случая параллельного выполнения. К счастью, он допускает естественное распараллеливание. Более того, распараллеливание можно вести на двух уровнях. Во-первых, интервал интегрирования можно разбить на р отрезков и независимо вычислять интеграл на соответствующем отрезке. Далее останется только суммировать полученные значения. При этом на каждом отрезке можно использовать одну и ту же последовательную версию. Поскольку объем требуемой работы на каждом отрезке уменьшается, то при параллельном выполнении можно ожидать уменьшения общего объема работы.

Распараллеливание можно продолжить, если вместо последовательной версии вычисления интеграла использовать версию, распараллеливающую процесс вычисления суммы. О том, как можно распараллелить конечную сумму, достаточно подробно сказано в предыдущих разделах этой главы.

Приведу метод, в котором распараллеливание ведется за счет разбиения интервала интегрирования на p отрезков:

/// <summary>
        /// Последовательный алгоритм
        /// Вычисление с разбиением интервала интегрирования
        /// на p сегментов
        /// </summary>
        public void SequenceIntegralWithSegments()
        {           
            double dx = (b - a) / p;           
            double start = 0, finish = 0;
            for (int i = 0; i < p; i++)
            {
                start = a + i * dx;
                finish = start + dx;
                DefiniteIntegral(start,
                   finish, out results[i]);
            }
            result = 0;
            for (int i = 0; i < p; i++)
            {
                result += results[i];
            }
        }

В цикле по числу отрезков вызывается последовательный алгоритм, вычисляющий значение интеграла на соответствующем отрезке. Этот цикл допускает распараллеливание. При наличии нескольких процессоров все они могут параллельно вычислять интеграл на своем отрезке интегрирования.

Заметьте, этот вариант алгоритма оказывается предпочтительнее и в случае проведения вычислений одним процессором. Причина в том, что на разных отрезках интегрирования функция может вести себя по-разному. Поскольку для каждого отрезка эффективно подбирается свое число N - число разбиений интервала интегрирования в методе прямоугольников, то общее время решения задачи может быть уменьшено.