Параллельные алгоритмы

Вычисление числа ПИ

Для параллельных вычислений классической тестовой задачей является задача вычисления числа ПИ. Обсудим и мы некоторые алгоритмы решения этой задачи, тем более что вся необходимая подготовка для ее решения уже выполнена.

Число ПИ и тригонометрические функции

Число ПИ естественным образом появляется при вычислении тригонометрических функций. Поскольку синус тридцати градусов равен одной второй, то вычислить ПИ можно по формуле:

( 3.15)

Ранее мы рассмотрели алгоритм вычисления функции ArcSin, способы распараллеливания этого алгоритма, и трудности, возникающие при распараллеливании.

Число ПИ и определенный интеграл

Вспомним, чему равна производная функции ArcTg(x)

( 3.16)

Отсюда непосредственно следует:

( 3.17)

Опять-таки, интеграл мы уже умеем считать, и знаем, как можно распараллелить алгоритм вычисления.

Существует и множество других разложений, позволяющих вычислить число ПИ с некоторой точностью. Одно из них в качестве примера использовалось нами при рассмотрении алгоритмов суммирования рядов (алгоритмы 3.5 и 3.6).

Алгоритмы линейной алгебры

Многие алгоритмы линейной алгебры легко распараллеливаются достаточно естественным образом. Все суперкомпьютеры при анализе их эффективности проходят тест Linpack, представляющий пакет различных алгоритмов линейной алгебры. Давайте рассмотрим некоторые классические алгоритмы линейной алгебры и обсудим возможности их распараллеливания.

Умножение матриц

Пусть матрица C размерности [m, n] является произведением двух прямоугольных матриц A и B, имеющих соответственно размерности [m, q] и [q, n]. Каждый элемент матрицы C является скалярным произведением двух векторов, заданных соответствующей строкой матрицы A и столбца матрицы B:

( 3.18)

Очевидно, что временная сложность последовательного алгоритма равна:

( 3.19)

Что может дать распараллеливание? В идеальном случае, когда у нас в распоряжении суперкомпьютер или, еще лучше, метакомпьютер с неограниченным числом процессоров, все элементы матрицы C можно считать параллельно, что в m*n раз сокращает время вычислений. Если же для вычисления суммы (3.18) применять пирамидальный алгоритм, то сложность умножения матриц становится равной:

Ускорение сверхзамечательное, но и его можно улучшить! Если использовать векторные процессоры, то вычисление скалярного произведения (3.18) становится элементарной операцией и тогда:

Все прекрасно. Одна беда - эффективность крайне низкая, поскольку потребуется m*n*q/2 векторных процессоров. Конечно же, если задача важна, а именно такие задачи решаются на суперкомпьютерах, то ускорение важнее эффективности.

Если же в нашем распоряжении есть компьютер с конечным и относительно небольшим числом процессоров - p, существенно меньшим m, то время умножения матрицы можно сократить в p раз. Распараллеливание проще всего выполнить естественным образом, разбив матрицу A на полосы примерно одинаковой ширины. Если m не кратно p, то ширина полос может отличаться на единицу. Если например p равно 8, а n - 100, то четыре полосы могут иметь по 12 строк, а другие четыре полосы - по 13 строк. Каждый из 8 процессоров будет выполнять умножение своей полосы на матрицу B, получая соответствующую полосу матрицы C. В результате их совместной и параллельной работы задача умножения матриц будет решена. Алгоритм распараллеливания настолько прост, что я не буду приводить его код. По сути, он немногим отличается от последовательного алгоритма.

Алгоритм умножения слабо заполненных матриц

Давайте рассмотрим более интересную задачу умножения слабо заполненных матриц, у которых большинство элементов равны нулю. Это позволит нам рассмотреть алгоритмы со сложно организованными данными, использующими не только массивы, но и списки и структуры. Когда на практике приходится иметь дело с очень большими матрицами, то как правило они являются слабо заполненными. Иногда они могут иметь специальную блочную структуру с нулевыми блоками. Но будем рассматривать общий случай, не учитывающий возможную структуру строения матрицы.

Слабо заполненную матрицу будем хранить в виде массива из n элементов. В зависимости от того, как мы хотим хранить матрицу - по строкам или по столбцам, параметр n будет задавать число строк или число столбцов матрицы, и каждый элемент массива задает соответственно строку или столбец слабо заполненной матрицы. Каждый элемент этого массива представляет собой список структур. Каждая структура хранит два числа - значение ненулевого элемента и его индекс в строке или в столбце.

Если перемножаемые матрицы A и B заполнены на 10%, то такое представление матриц позволяет примерно в 5 раз сократить требуемую для их хранения память. Существенно сократится и время умножения матриц, поскольку все действия будут выполняться только над ненулевыми элементами.

Будем предполагать, что нули равномерно распределены в слабо заполненной матрице. Пусть p - вероятность того, что элемент такой матрицы не равен нулю, и эта вероятность мала. Что можно сказать о степени заполнения матрицы C = A * B? Нетрудно видеть, что для больших значений n произведение слабо заполненных матриц этим свойством обладать не будет. Вероятность того, что элемент матрицы C не равен нулю, можно посчитать по формуле:

( 3.20)

При n = 100 и p = 0,1 вероятность 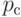= 0,634, но при n = 1000 она практически приближается к единице и равна 0,9999.

Ситуация меняется, если вероятность p является убывающей функцией от n. Пусть, например, p = 1/n, тогда

( 3.21)

Учитывая соотношения (3.20) и (3.21), можно сформулировать следующее утверждение:

Теорема:

Если при умножении слабо заполненных матриц A и B вероятность ненулевого элемента p постоянна, то с ростом размера матриц n вероятность заполнения результирующей матрицы C стремится к единице.

Если при умножении слабо заполненных матриц A и B вероятность ненулевого элемента p зависит от n и равна 1/n, то результирующая матрица C также является слабо заполненной с той же вероятностью заполнения, как и исходные матрицы .

Из теоремы следует, что разумно строить разные алгоритмы, для случая, когда произведение умножаемых матриц является плотно заполненной матрицей, и для случая, когда это произведение является слабо заполненной матрицей.

Начнем с первого случая и построим алгоритм для случая умножения слабо заполненных матриц, полагая, что их произведение является плотно заполненной матрицей. Первый сомножитель - матрицу A - будем хранить по строкам, а второй сомножитель - матрицу B - по столбцам. Каждую из этих матриц будем представлять в виде одномерного массива, элементы которого являются списками с ненулевыми элементами соответствующих строк и столбцов. Результирующая матрица C будет представлена традиционным способом в виде двумерного массива. Вот пример возможной программы на C#:

/// <summary>
        /// Умножение слабо заполненных матриц
        /// [n * m] * [m * q] = [n * q]
        /// </summary>
        /// <param name="A"></param>
        /// <param name="B"></param>
        /// <param name="C"></param>
        public void MultMatr(ArrayList[] A, ArrayList[] B, double[,] C)
        {           
            ArrayList listA, listB;
            Item itemA, itemB;
            int na = 0, nb = 0;
            int ia = 0, ib = 0;
            //Цикл по числу строк матрицы А
            for(int i =0; i < A.Length; i++)
            {
                listA = A[i];   //i-я строка А как список ненулевых элементов
                na = listA.Count;
                // Цикл по числу столбцов матрицы В
                for (int j = 0; j < B.Length; j++)
                {
                    listB = B[j];   //j-й столбец
                    nb = listB.Count;
                    ia = 0; ib = 0;
                    C[i, j] = 0;
                    while (ia < na & ib < nb)
                    {
                        itemA = (Item)listA[ia];
                        itemB = (Item)listB[ib];
                        if (itemA.index == itemB.index)
                        {
                            C[i, j] += itemA.val * itemB.val;
                            ia++;                           
                            ib++;                            
                        }
                        else
                            if (itemA.index < itemB.index)
                                ia++;                 
                            else
                                ib++; 
                    }
                }
            }
        }

Циклы for в этой программе допускают распараллеливание, позволяя все элементы результирующей матрицы C считать параллельно и одновременно. Понятно, что внутренний цикл while требует последовательного выполнения. Поэтому, если бы в нашем распоряжении были бы n*m свободных процессоров, то время вычисления матрицы C определялось бы временем работы внутреннего цикла и зависело бы как от размера матриц n, так и от вероятности заполнения, так что временную сложность можно было бы представить как O(p * n).

Следует отметить, что эта программа является оптимальной и для случая ее выполнения одним процессором.

Если ориентироваться на многоядерные компьютеры с фиксированным числом процессоров, то разумно рассмотреть алгоритм, предполагающий управляемое программистом распараллеливание. В этом случае естественный способ распараллеливания состоит в разбиении исходной матрицы A на полосы. Каждый процессор для умножения своей полосы может использовать выше приведенный алгоритм умножения прямоугольных матриц.

Вот пример возможной записи такой программы на C#:

/// <summary>
 /// Умножение слабо заполненных матриц
 /// [n * m] * [m * q ] = [n * q]
 /// Умножение идет p полосами 
 /// Предполагается, что каждую полосу умножает один процессор
 /// </summary>
 /// <param name="A"></param>
 /// <param name="B"></param>
 /// <param name="C"></param>
 /// <param name="p">число полос</param>
 public void MultMatrBar(ArrayList[] A, ArrayList[] B, double[,] C, int p)
        {          
            int n, m, q;
            n = A.Length;
            m = n / p;
            ArrayList[] barA = new ArrayList[m];
            q = B.Length;
            double[,] barC = new double[m, q];

            //Цикл по числу полос кроме последней
            for (int i = 0; i < p - 1; i++)
            {
                Array.Copy(A, i * m, barA, 0, m);
                MultMatr(barA, B, barC);
                Array.Copy(barC, 0, C, i * q, m * q); 
            }
            // ширина последней полосы
            // может отличаться 
            n = n - m * (p - 1);
            barA = new ArrayList[n];
            barC = new double[n, q];
            Array.Copy(A,(p - 1) * m, barA, 0, n);
            MultMatr(barA, B, barC);
            Array.Copy(barC, 0, C, (p - 1) * q, n * q); 
        }

Оставляю читателям в качестве упражнения написать алгоритмы и разработать соответствующие программы для случая, когда матрица C является слабо заполненной и представляется массивом списков, содержащих только ненулевые элементы этой матрицы.