Параллельные вычисления

Свойства параллельных вычислений

В предыдущем разделе введены три параметра, характеризующие модель параллельных вычислений, - 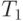, , 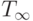- и заданы некоторые соотношения между ними. Продолжим эту тему и введем еще ряд характеристик. Все вводимые характеристики рассматриваются как функции параметра n, характеризующего сложность решаемой задачи. Обычно n понимается как объем входных данных.

Ускорение

Ускорение 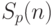определяют как отношение:

( 1.24)

Важно правильно интерпретировать это отношение. Числитель и знаменатель, вообще говоря, рассчитываются для двух разных алгоритмов. Когда задача ориентирована на выполнение одним процессором, то можно построить алгоритм, оптимальный для последовательного выполнения. Использование нескольких процессоров, одновременно ведущих вычисления, требует другого алгоритма, предусматривающего распараллеливание. Построение хороших параллельных алгоритмов - это не простая задача. Чаще всего, хороший последовательный алгоритм не является таковым для параллельного выполнения.

Если у нас есть некоторая задача, и речь идет о том, какого ускорения можно добиться при распараллеливании, то в формуле (24) следует сравнивать время наилучшего последовательного алгоритма, для которого достаточно одного процессора, и время наилучшего параллельного алгоритма, который может использовать p имеющихся процессоров.

Какое ускорение является оптимальным? Ответ на этот вопрос дают оценки для , полученные в предыдущем разделе. Из нижней оценки следует, что ускорение не может превосходить числа процессоров:

( 1.25)

Иногда эта оценка нарушается, и ускорение реально может быть больше p. В этом случае говорят о гиперускорении. Гиперускорение может возникнуть, если добавление процессоров влияет не только на вычисления. Например, появляется дополнительная память, возможно, другие устройства, способствующие ускорению решения задачи.

Максимальное ускорение для задачи задается соотношением:

( 1.26)

Эффективность

Эффективность определяют как отношение:

( 1.27)

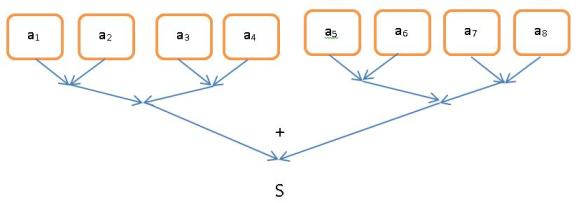
Добиваться высокого ускорения следует, но не любой ценой. При оптимальном ускорении эффективность равна 1. Если же эффективность существенно ниже 1, то часто число процессоров целесообразно уменьшить, используя их более эффективно. Поясним ситуацию примером. Рассмотрим классическую задачу вычисления суммы элементов массива. Последовательный алгоритм, используя один процессор, вычисляет сумму за время порядка O(n). Схема вычисления показана на Рис. 1.3

Рис. 1.3. Последовательное суммирование

Вычисление суммы можно распараллелить, построив пирамидальный алгоритм, который будет вычислять сумму за время O(log n), но для него на первом шаге потребуется n/2 процессоров, которые будут вычислять суммы пар элементов массива. На следующем шаге, число процессоров сократится вдвое, когда вычисляются суммы четверок. Для получения окончательного результата на последнем шаге потребуется всего один процессор. Схема вычисления показана на Рис. 1.4

увеличить изображение
Рис. 1.4. Схема пирамидального параллельного алгоритма вычисления суммы элементов

Ускорение для этого алгоритма при вычислении суммы большого числа элементов прекрасное:

При n, равном 2²⁰, например, ускорение более 2¹⁵, составляет десятки тысяч раз. Но и процессоров требуется такого же порядка. Посчитаем эффективность для этого случая:

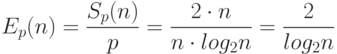
Для нашего примера эффективность будет равна 0,1. Возможно, более разумно в этой ситуации использовать конечное число процессоров. Например, имея 16 процессоров, можно разделить массив на 16 частей, для каждой из них процессоры вычислят частные суммы, а потом останется сложить эти частные суммы. В этом случае ускорение будет равно 16, но эффективность практически равна 1.

Упущенная эффективность

На проблему эффективности можно смотреть и с другой точки зрения. Пусть в нашем распоряжении есть многоядерный компьютер. Возникает естественный вопрос, насколько эффективно используются его возможности?

Введем в рассмотрение меру неиспользованных возможностей - упущенной выгоды - U(n), определив ее следующим образом:

( 1.28)

Полагая, что оптимальное время, которое можно достичь, используя p процессоров, дается нижней оценкой для , получим:

( 1.29)

Если для компьютера с p ядрами время решения задачи оптимально и сокращается в p раз в сравнении с решением задачи на одноядерном компьютере, то наши потери равны нулю, возможности компьютера полностью используются. Если же задача решается за время 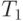- столь же долго, как на одноядерном компьютере, то потери пропорциональны числу неиспользованных ядер.