Параллельные вычисления

Теорема_1

Время 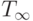задается максимально нагруженным путем в графе зависимостей.

Прежде всего, докажем, что при неограниченном числе процессоров оптимальное расписание каждого процессора содержит не более одного модуля на каждом уровне. Доказательство дается индукцией по числу уровней. Для уровня 1 утверждение справедливо, поскольку на этом уровне число процессоров совпадает с числом модулей этого уровня для оптимального расписания. Пусть утверждение справедливо на уровне j. Покажем, что оно остается справедливым и для модулей следующего уровня j + 1. Действительно, рассмотрим процессор Pr, выполняющий i-й модуль уровня j - . Когда этот процессор завершит работу, то может оказаться, что появятся готовые к выполнению m модулей уровня j +1, ожидавших завершения работы . Только один из этих модулей включается в оптимальное расписание процессора Pr, а остальные будут включены в расписание свободных процессоров, участвующих в работе. Если таковых не окажется, то всегда можно добавить новые процессоры, так что все модули, ожидавшие завершения работы модуля , начнут выполняться одновременно. Отсюда по индукции следует справедливость утверждения для всех уровней. Отсюда же следует, что 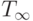не может быть больше времени, задаваемого критическим путем.

Покажем теперь, что оптимальное расписание может быть составлено таким образом, чтобы критический путь был назначен одному процессору. Пусть процессор Ps - тот процессор, которому назначен 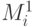первого уровня, лежащий на критическом пути. Спускаясь по уровням, этому процессору будем назначать модуль, лежащий на критическом пути. Так построенное расписание сохраняет свойство оптимальности, поскольку процессор Ps не простаивает, и ни какой другой процессор не может начать выполнять модули, лежащие на критическом пути, раньше процессора Ps. Заметьте, критический путь, вообще говоря, может быть не единственным.

Сложнее получить формулу для вычисления . Проблема составления оптимального расписания в этих условиях относится к NP - полным проблемам, что означает, отсутствие алгоритма полиномиальной сложности, и для решения задачи необходимы переборные алгоритмы. Этим мы не будем заниматься.

Займемся тем, что покажем справедливость ранее полученных оценок (8) для в случае, когда время выполнения модулей различно и в графе зависимостей для каждого модуля задано время его работы:

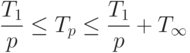( 1.12)

Дадим вначале графическую интерпретацию. Задание нижней и верхней оценки для означает, что эта функция ограничена двумя гиперболами. Функция убывающая. В начальной точке при p=1 по определению , так что функция находится в заданном коридоре. Это же справедливо и для конечных точек, для всех p, больших некоторого значения p*, при котором . Остается показать, что утверждение верно и для остальных значений 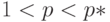. Рис. 1.2 иллюстрирует поведение .

увеличить изображение
Рис. 1.2. Поведение функции Tp(p)

Приведем пример. Рассмотрим двух уровневую систему модулей, граф зависимостей которых показан на Рис. 1.1.

Нетрудно посчитать, что в этом случае:

Для случая двух процессоров для этого конкретного примера несложно задать оптимальное расписание. Для первого процессора последовательность выполняемых им модулей может быть следующей:

Для второго процессора последовательность следующая:

Время работы первого процессора равно 15, второго - 15. Следовательно, 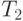равно 15. Критический путь входит в расписание второго процессора. Подключение второго процессора в этой задаче позволяет вдвое уменьшить время выполнения в сравнении со случаем использования только одного процессора. Подключение третьего процессора, хотя и не столь эффективно, но позволит свести время выполнения до минимально возможного результата - 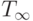. Добавление других процессоров не имеет смысла, поскольку не позволяет сократить время решения задачи.

После рассмотрения примера, перейдем к получению оценок.

Оценка снизу

Лемма 1

Для справедлива оценка

( 1.13)

Докажем справедливость оценки. Пусть p процессоров выполняют работу согласно оптимальному расписанию, и ни один из процессоров не простаивает до окончания всей работы. Поскольку в результате все модули будут выполнены, и ни один модуль не будет выполняться дважды, то суммарное время работы всех процессоров равно :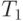

( 1.14)

Поскольку - это максимальное значение, затраченное одним из процессоров, на выполнение своей работы:

( 1.15)

Справедливость нижней оценки

( 1.16)

следует из общих свойств суммы компонентов. Максимальный компонент всегда больше или равен среднего арифметического значения суммы.

Если некоторые процессоры могут простаивать, то время может только увеличиваться, что гарантирует выполнения условия (16).

Равенство достигается в единственном случае, когда все компоненты суммы имеют одно и то же значение. Содержательно это означает, что все процессоры одновременно начинают свою работу и одновременно ее заканчивают. В этом случае общее время выполнения работы сокращается в p раз.

Оценка сверху

Пусть работу выполняют p процессоров. Составление расписания означает, что граф зависимостей разбивается на p непересекающихся подграфов. Все модули каждого из подграфов выполняются одним процессором. Подграф с максимальным временем выполнения для данного разбиения будем называть максимально нагруженным подграфом. Оптимальное расписание предполагает такое разбиение, при котором максимально нагруженный подграф выполняется за минимально возможное время. Итак, будем предполагать, что граф зависимостей G разбит на непересекающиеся подграфы :

( 1.17)

Не снижая общности, будем полагать, что максимально нагруженным подграфом является подграф .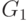

Лемма 2

Для справедлива оценка

( 1.18)

Доказательство от противного. Покажем, что в этом случае разбиение не является оптимальным и может быть улучшено, что приведет к уменьшению времени .

Итак, предположим, что

( 1.19)

Отсюда следует:

( 1.20)

Пусть 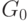- минимально нагруженный подграф, тогда время его выполнения не больше среднего времени выполнения, так что имеем:

( 1.21)

Подграфу 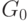можно передать часть работ подграфа 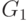, уменьшив суммарное время работы. Действительно, подграф 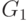можно представить в виде:

( 1.22)

Здесь Path это часть пути или некоторый путь, начинающийся на первом уровне, который заведомо меньше критического пути. При передаче его подграфу 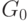время выполнения этого подграфа останется меньше времени выполнения подграфа 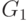. Общее время выполнения работ при этом уменьшится. Следовательно, пришли к противоречию с утверждением об оптимальности расписания, что доказывает справедливость соотношения:

( 1.23)

В заключение дадим некоторые практические рекомендации, следующие из полученных оценок. Выигрыш, который можно получить, используя дополнительные процессоры, зависит от разницы между общим временем выполнения всех модулей программы - 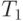и временем выполнения критического пути в графе зависимостей - .

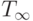Эта разница максимальна для крайнего случая, когда все модули могут выполняться независимо, и в графе зависимостей все модули находятся на одном первом уровне. Критический путь в этом случае состоит из одного модуля, требующего максимального времени своего выполнения. Так что 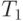- это время выполнения всех модулей, а 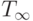- это время выполнения одного модуля. Привлечение p процессоров может дать существенный эффект, уменьшая время выполнения практически до среднего времени выполнения одного модуля .

Эта разница минимальна для другого крайнего случая - строго последовательной программы, когда N модулей программы расположены на N уровнях, и критический путь задает выполнение всех модулей. В этом случае 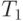и 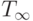совпадают и, как следствие, равно 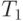при любом числе процессоров, так что привлекать дополнительные процессоры в этом случае бессмысленно.

Для строго последовательной программы, когда i-й модуль зависит от модуля i-1, все три характеристики будут совпадать. Для строго последовательной программы дополнительные процессоры не позволяют уменьшить время выполнения программы в сравнении со временем выполнения этой же программы одним процессором. Так, например, задача о "Ханойской башне" на суперкомпьютере с сотнями тысяч процессоров будет решаться столь же долго, как и на компьютере с одним процессором. Это вытекает из сути задачи, - перенос следующего кольца требует завершение переноса предыдущего кольца, - параллельно эту работу выполнять нельзя.