Параллельные вычисления

Оценки ускорения. Законы Амдаля и Густавсона - Барсиса

Ранее получены оценки для времени решения задачи при использовании p процессоров. При этом предполагалось, что задачу можно разделить на модули, задав граф зависимостей, определяющий возможный порядок вызова модулей. Представляет интерес рассмотрения случая, когда задачу можно разделить на две части, из которых одна часть требует последовательного выполнения, а вторая может быть полностью распараллелена. Законы Амдаля и Густавсона - Барсиса позволяют получить оценки для ускорения в зависимости от доли последовательных вычислений в общем времени решения задачи. Законы отличаются лишь тем, как определяется доля последовательных вычислений.

Закон Амдаля

Пусть время решения задачи одним процессором можно представить как сумму времен решения последовательной части и части, допускающей распараллеливание:

Разделив обе части уравнения на 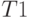, перейдем к долям времени:

Время решения задачи p процессорами также представим двумя частями:

Последовательную долю нельзя уменьшить увеличением числа процессоров, поэтому . Для параллельной части существует оценка, так что имеет место соотношение:

Переходя к ускорению, получим:

( 1.30)

Соотношение (30) называется законом Амдаля. Оно говорит, что ускорение ограничено сверху величиной, зависящей от доли последовательных вычислений. Если, например, последовательные вычисления занимают 10% от общего времени вычисления, то за счет распараллеливания нельзя добиться более чем десятикратного ускорения времени работы, сколь много процессоров бы не привлекалось.

Пессимистический характер закона Амдаля может быть сглажен, если вспомнить, что все характеристики следует рассматривать, как функции от n - параметра характеризующего объем используемых данных. В этом случае закон Амдаля выглядит так:

( 1.31)

На практике часто бывает, что последовательная часть задачи постоянна и не зависит от объема данных. В этом случае q(n) - убывающая функция, тогда для больших n можно добиться хорошего ускорения, не вступая в противоречие с законом Амдаля.

Закон Густавсона -Барсиса

Запишем оптимальное время работы при использовании p процессоров в виде суммы времен двух частей - параллельной и последовательной:

С учетом того, что последовательная часть выполняется p процессорами столь же долго, как одним процессором, а время параллельной части в оптимальном случае можно уменьшить в p раз, получим:

Разделив обе части уравнения на , перейдем к долям времени:

Рассмотрим теперь отношение:

Переходя к ускорению, получим

( 1.32)

Соотношение (32) выражает закон Густавсона-Барсиса, задавая оценку сверху для ускорения. Когда доля g стремится к единице, то и ускорения нет, оно ограничено единицей. Если же доля стремится к нулю, то ускорение, как и положено, ограничено числом используемых процессоров p.

Как и в законе Амдаля, характеристики следует рассматривать как функции параметра n:

( 1.33)

Два способа распараллеливания

Говоря о распараллеливании, различают два основных способа, позволяющих проводить параллельные вычисления, - распараллеливание по задачам и распараллеливание по данным.

Модель, рассмотренная выше, соответствовала случаю распараллеливания по задачам. В этой модели разные модули одной программы могли выполняться параллельно.

Рассмотрим теперь альтернативную ситуацию, когда выполняется распараллеливание по данным. В этом случае некоторое множество данных необходимо обработать одним модулем.

Распараллеливание по данным

Пусть необходимо решить задачу D на некотором конечном множестве данных . Зачастую, эффективный последовательный алгоритм решения этой задачи можно получить, если удается свести решение исходной задачи к решению k подзадач - , где каждая подзадача означает решение исходной задачи D, но на подмножестве данных . Наиболее эффективно, когда все подзадачи имеют один и тот же размер.

Справедлива простая, но крайне важная в теории алгоритмов

Теорема:

Если задачу D(X) можно свести к решению k подзадач одинаковой размерности и за линейное время из решений k подзадач можно получить общее решение исходной задачи, то временная сложность решения исходной задачи T(n) дается формулой:

( 1.34)

Здесь с - некоторая константа.

Для простоты будем полагать, что . Тогда с учетом сделанных предположений

Продолжая разворачивать этот процесс, дойдем до времени T(1), которое можно считать без ограничения общности константой, равной c. Таким образом, получим:

( 1.35)

Эффективный последовательный алгоритм предполагает рекурсивное определение. За счет сведения исходной задачи к решению нескольких задач меньшей размерности удается существенно снизить временную оценку сложности решения задачи в сравнении со случаем, когда задача решается для полного набора данных.

Классическим примером являются алгоритмы сортировки. В сортировке слиянием исходное множество разделяется на два подмножества практически одинаковой мощности (размер может отличаться на единицу). Слияние двух отсортированных подмножеств можно выполнить за линейное время. Поэтому временная сложность этой сортировки в соответствии с соотношением (35) задается формулой . В то же время сложность таких простых алгоритмов сортировки как, например, пузырьковая сортировка задается соотношением . При больших n, например при , время сортировки слиянием может быть в тысячи раз меньше времени пузырьковой сортировки.

Этот пример показывает, что и последовательные алгоритмы могут эффективно использовать распараллеливание по данным. А что могут дать в этой ситуации параллельные алгоритмы, использующие наличие k процессоров.

Пусть у нас есть компьютер, имеющий k ядер, и нужно решить задачу на множестве данных размерности . Самое простое решение состоит в том, чтобы разбить исходное множество на k подмножеств одинаковой размерности . Затем применять эффективный рекурсивный последовательный алгоритм, решая параллельно на всех ядрах исходную задачу для соответствующего подмножества. После этого за линейное время объединить полученные решения. Учитывая ранее полученные соотношения, временная сложность такого алгоритма дается соотношением:

( 1.36)

Сравнивая соотношения (35) и (36), можно видеть, что за счет использования k ядер можно в k раз уменьшить сложность алгоритма. Заметьте, рассматриваемая версия алгоритма использует рекурсию только в последовательной версии, запускаемой на каждом ядре. Использование рекурсии в параллельных алгоритмах не всегда приводит к повышению эффективности.