|
Добрый день. Вопрос №1 Какова стоимость получения диплома о мини-МБА по данному курсу? Или ориентироваться на указанную на сайте? Вопрос №2 Возможно ли начать обучение без потери результатов, не отправив документы на зачисление, а отправку выполнить позже? |
Тестовые примеры. Классы эквивалентности. Ручное тестирование в MVSTE
5.1. Проверка домашнего задания
Обсуждение спецификации на программу "Калькулятор". Студенты описывают выявленные в спецификации ошибки и обосновывают их. Студентам выдается правильная версия спецификации.
5.2. Тестовые примеры
5.2.1. Разработка тестовых примеров
Непосредственно для тестирования программного обеспечения необходимо определить проверочные задания, выполняемые системой или ее отдельной частью. Такие задачи называются тестовыми примерами.
Можно выделить два подхода к созданию тестовых примеров – исходя из функциональных требований (или из любой другой документации описывающей систему) и исходя из кода. Построение тестовых примеров, исходя из кода, и построение покрытия кода мы будем изучать позднее, а сейчас рассмотрим подробнее первый случай. При тестировании функциональности программы применяется подход "черного ящика", то есть для каждого требования к системе формируются тест-требования, которые, как правило, детализируют функциональные требования так, что на одно функциональное требование может приходиться несколько тест-требований. Сами тест-требования определяют, что должно быть протестировано, но не определяют, как. Конкретные значения задаются в тестовых примерах. Таким образом, одному тест-требованию может соответствовать сразу несколько тестовых примеров.
Каждый тестовый пример состоит из набора входных значений и набора ожидаемых выходных значений. Рассмотрим спецификацию из "Место верификации среди процессов разработки программного обеспечения" .
Начнем мы с тестирования отдельных составляющих программы (в данном случае – модуль математика) на допустимые данные и, в частности, на допустимые граничные данные.
Рассмотрим пример. Для этого возьмем требование 4.2.4.1.
Требование 4.2.4.1: Для чисел, меньших либо равных MAXINT и больших либо равных MININT, частное которых меньше либо равна MAXINT и больше либо равна MININT и делитель не равен 0, функция деления должна возвращать правильное частное с точки зрения математики.
Функция, которую будем тестировать:
/// <summary>
/// частное
/// </summary>
/// <param name="a">делимое</param>
/// <param name="b">делитель</param>
/// <returns>частное</returns>
public static long Div(long a, long b)В принципе, тестирование такой функции легко автоматизируется при помощи Unit Testing, так как у нее уровень доступа public, т.е. к ней можно обратиться из любого класса. К тому же она является статической, что позволит вызывать ее, не создавая экземляр класса CalcClass. Однако на этом семинаре мы рассмотрим ручное тестирование.
Прежде всего по этому функциональному требованию составим тест-требования. На первый взгляд, очевидно, что вопрос для проверки звучит так: "Проверить, что для чисел, меньших либо равных MAXINT и больших либо равных MININT, частное которых меньше либо равно MAXINT и больше либо равно MININT и делитель не равен 0, функция деления возвращает правильное частное с точки зрения математики". Однако, это не совсем так. Фраза "меньших либо равных" сразу же наводит на мысль о проверке двух случаев – 1) хотя бы одно из чисел строго равно MAXINT и 2) все числа меньше, чем MAXINT.
Замечание. Стоит заметить, что сейчас мы пишем очень подробные тест-требования, которые практически сразу можно отобразить в тестовые примеры. Такая ситуация наблюдается, например, в проектах, в которых тест-требования отсутствуют, а тестовые примеры пишутся сразу на основании функциональных требований.
Тест-требования
- Проверить, что для чисел, меньших MAXINT и больших 0, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делимого, меньшего MAXINT и большего 0, и делителя, меньшего 0 и большего MININT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делимого, меньшего 0 и большего чем MININT, и делителя, большего 0 и меньшего MAXINT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для чисел, меньших 0 и больших MININT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делимого, равного 0, и делителя, меньшего MAXINT и большего 0, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делимого, равного 0, и делителя, большего MININT и меньшего 0, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делимого, равного MAXINT, и делителя, меньшего MAXINT и большего MININT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делимого, равного MININT, и делителя, меньшего MAXINT и большего MININT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делителя, равного MAXINT, и делимого, меньшего MAXINT и большего MININT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делителя, равного MININT, и делимого, меньшего MAXINT и большего MININT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делителя, равного MAXINT, и делимого, равного MININT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делителя, равного MAXINT, и делимого, равного MAXINT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делителя, равного MININT, и делимого, равного MININT, функция деления возвращает правильное частное с точки зрения математики.
- Проверить, что для делителя, равного MININT, и делимого, равного MAXINT, функция деления возвращает правильное частное с точки зрения математики.
Замечание: на самом деле, еще можно проверить, что функция корректно работает с однозначными и многозначными числами. К тому же надо убедиться, что она правильно обрабатывает все цифры в числах, а, например, не генерирует исключение, если одно из чисел содержит цифру 9, или результат ее работы не зависит от того, делится ли одно число на другое нацело или нет.
Составим тестовые примеры и запишем их в виде таблицы (табл.5.1).
| № | Входные значения: делимое, делитель | Ожидаемый результат | Номер тест-требования | Примечания |
|---|---|---|---|---|
| 1) | 43 / 21 | 2 | 1) | Самый частый случай – корректные входные данные |
| 2) | 87/-56 | -1 | 2) | -//- |
| 3) | -9/2 | -4 | 3) | -//- |
| 4) | -4321/-50 | 86 | 4) | -//- |
| 5) | 0/1234567890 | 0 | 5) | Часто ошибки проявляются при нулевых значениях переменных |
| 6) | 0/-1098765432 | 0 | 6) | -//- |
| 7) | 2147483647/95 | 22605091 | 7) и 1) | Проверка граничных условий |
| 8) | -2147483648/9 | -238609294 | 8) и 2) | -//- |
| 9) | 99/2147483647 | 0 | 9) и 1) | -//- |
| 10) | -87/-2147483648 | 0 | 10) и 4) | -//- |
| 11) | -2147483648/2147483647 | -1 | 11) | А здесь - ошибка |
| 12) | 2147483647/2147483647 | 1 | 12) | -//- |
| 13) | -2147483648/-2147483648 | 1 | 13) | Ошибка |
| 14) | 2147483647/-2147483648 | 0 | 14) | Ошибка |
Примечание. Здесь стоит так или иначе сымитировать работу функции и исследовать ее функциональность вместе со студентами.
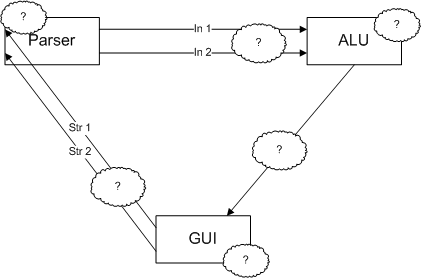
Заметим, что, мы не можем точно сказать, где произошла ошибка, — это хорошо видно из рис.5.1.
Части рисунка, помеченные вопросом – те части программы, в которых могла быть ошибка. Это сами вычисления, преобразование типов, ошибка GUI или передачи параметров (возможно, с некорректным преобразованием типов). О выявленных ошибках составляется отчет, который отдается разработчикам. При этом исправление ошибки в обязанности тестировщика не входит, так как он занимается именно тестированием, а не отладкой приложения.
В первом тесте мы ввели два числа и получили верный результат. Все остальные тесты точно такие же. Но перебрать их все не получится, так как всевозможных комбинаций – 429496736 * 429496735= 184467445805156960. Очевидно, что большинство входных значений приведут к одному и тому же результату, и нет смысла проверять их все. Если программа пройдет первый тест, то она, вероятнее всего, пройдет и остальные.
Если от двух тестовых примеров ожидается получить один и тот же результат, значит, они принадлежат одному классу. Такие множества примеров называются классами эквивалентности. Классы эквивалентности — это, в первую очередь, способ уменьшения необходимого числа тестовых примеров. При тестировании достаточно выполнить только один тестовый пример для каждого класса эквивалентности. Разбиение на классы эквивалентности особенно полезно, когда на вход системы может быть подано большое количество различных значений; тестирование каждого возможного значения привело бы к слишком большому объему тестирования.