|
Добрый день. Подскажите пожалуйста, я прошел ваш курс Введение в линейную алгебру: Информация, - сдал экзамен и у меня высветилось окно, где необходимо оформить доставку сертификата. Однако, я случайно закрыл это окно и теперь не могу найти этот подраздел, чтобы оформить доставку. Где можно это найти? |
Матрицы. Основные определения и виды матриц. Действия над матрицами. Понятие ранга матрицы. Операции над матрицами. Понятие и нахождение обратной матрицы
Матрицы. Основные определения и типы матриц
Определение 1. Матрицей A называется любая прямоугольная таблица, составленная из чисел aij, которые называют элементами матрицы и обозначается
 |
( 2.1) |
Заметим, что элементами матрицы могут быть не только числа. Представим себе, что вы описываете книги, которые стоят на вашей книжной полке. Пусть у вас на полке порядок и все книги стоят на строго определенных местах. Таблица, которая будет содержать описание вашей библиотеки (по полкам и следованию книг на полке), тоже будет матрицей. Но такая матрица будет не числовой. Другой пример. Вместо чисел стоят разные функции, объединенные между собой некоторой зависимостью. Полученная таблица также будет называться матрицей. Иными словами, Матрица, это любая прямоугольная таблица, составленная из однородных элементов. Здесь и далее мы будем говорить о матрицах, составленных из чисел.
Вместо круглых скобок для записи матриц применяют квадратные скобки или прямые двойные вертикальные линии
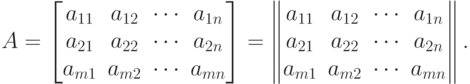 |
( 2.1*) |
Определение 2. Если в выражении (1) m = n, то говорят о квадратной матрице, а если 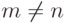 , то о прямоугольной.
, то о прямоугольной.
В зависимости от значений m и n различают некоторые специальные виды матриц:
-
Матрица - строка (или строковая матрица), состоящая из одной строки. Это прямоугольная матрица размером 1 x n.
A=(a11 a12 ... an).
-
Матрица - столбец ( столбцевая матрица), состоящая только из одного столбца. Это также прямоугольная матрица размером m x 1
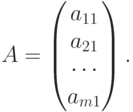
- Матрица, состоящая из одного элемента. A=(a11)1x1=a11.
-
Нулевая матрица, состоящая из одних нулей, в матричной алгебре играет роль 0, обозначается V.

-
Единичная матрица, состоящая из нулей, кроме главной диагонали, на которой стоят единицы. Обозначается E и играет роль единицы в матричной алгебре
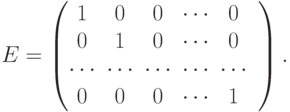
-
Диагональная матрица, квадратная порядка n, состоящая из нулей и на главной диагонали стоят не равные нулю элементы (не обязательно единицы)
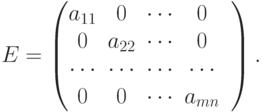
Важнейшей характеристикой квадратной матрицы является ее определитель или детерминант, который составляется из элементов матрицы и обозначается
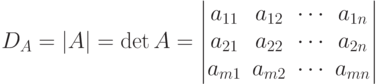
Очевидно, что DE=1 ; 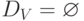 .
.
Определение 3. Если  , то матрица A называется невырожденной или не особенной.
, то матрица A называется невырожденной или не особенной.
Определение 4. Если detA = 0, то матрица A называется вырожденной или особенной.
Определение 5. Две матрицы A и B называются равными и пишут A = B, если они имеют одинаковые размеры и их соответствующие элементы равны, т.е.
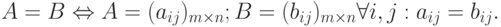
Например, матрицы 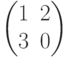 и
и 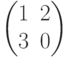 равны, т.к. они равны по размеру и каждый элемент одной матрицы равен соответствующему элементу другой матрицы. А вот матрицы
равны, т.к. они равны по размеру и каждый элемент одной матрицы равен соответствующему элементу другой матрицы. А вот матрицы 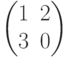 и
и  нельзя назвать равными, хотя детерминанты обеих матриц равны, и размеры матриц одинаковые, но не все элементы , стоящие на одних и тех же местах равны. Матрицы
нельзя назвать равными, хотя детерминанты обеих матриц равны, и размеры матриц одинаковые, но не все элементы , стоящие на одних и тех же местах равны. Матрицы 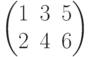 и
и 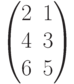 разные, так как имеют разный размер. Первая матрица имеет размер 2х3, а вторая 3х2. Хотя количество элементов одинаковое – 6 и сами элементы одинаковые 1, 2, 3, 4, 5, 6, но они стоят на разных местах в каждой матрице. А вот матрицы
разные, так как имеют разный размер. Первая матрица имеет размер 2х3, а вторая 3х2. Хотя количество элементов одинаковое – 6 и сами элементы одинаковые 1, 2, 3, 4, 5, 6, но они стоят на разных местах в каждой матрице. А вот матрицы 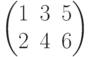 и
и 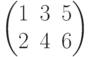 равны, согласно определению 5.
равны, согласно определению 5.
Определение 6. Если зафиксировать некоторое количество столбцов матрицы A и такое же количество ee строк, тогда элементы, стоящие на пересечении указанных столбцов и строк образуют квадратную матрицу n - го порядка, определитель которой 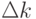 называется минором k – го порядка матрицы A.
называется минором k – го порядка матрицы A.
Пример. Выписать три минора второго порядка матрицы
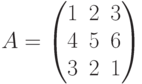
Решение. 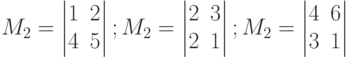 .
.
