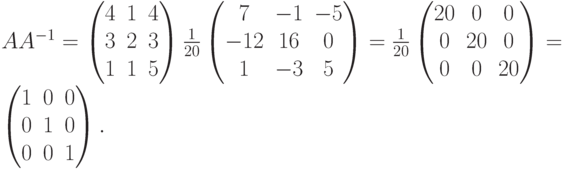НОУ ИНТУИТ | Введение в линейную алгебру. Лекция 3: Матрицы. Основные определения и виды матриц. Действия над матрицами. Понятие ранга матрицы. Операции над матрицами. Понятие и нахождение обратной матрицы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.10.2007 | Доступ: свободный | Студентов: 4493 / 787 | Оценка: 4.09 / 3.28 | Длительность: 11:25:00

Тема: Математика

Специальности: Математик

Теги: линейные пространства, метод Гауса, определители, векторы, матрицы

|

Вам нравится? Нравится 45 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Операции над матрицами

Определение 9. Суммой двух матриц одинакового размера A=(a_ij) и B=(b_ij) называется матрица C, у которой (c_ij)=(a_ij+b_ij), и записывают C = A + B.

Пример. Найти A + B, если

$A= \begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 2 & 1 & 0 \end{pmatrix}, \quad B= \begin{pmatrix} 1 & 0 & 1 \\ 0 & 0 & 1 \\ 3 & 2 & 0 \end{pmatrix}.$

Решение.

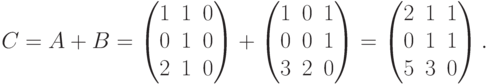
$C = A + B = \begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 2 & 1 & 0 \end{pmatrix} + \begin{pmatrix} 1 & 0 & 1 \\ 0 & 0 & 1 \\ 3 & 2 & 0 \end{pmatrix} = \begin{pmatrix} 2 & 1 & 1 \\ 0 & 1 & 1 \\ 5 & 3 & 0 \end{pmatrix}.$

Можно убедится самостоятельно в справедливости равенств

A + B = B + A ;
(A + B) + C = A + (B + C).

Определение 10. Произведением матрицы A=(a_ij) на число k называется такая матрица C=(c_ij), у которой (c_ij) = (ka_ij).

Для операции произведение матрицы на число справедливы следующие соотношения:

kA=Ak ;
k(A+B)=Ak+Bk ;
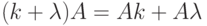$(k+\lambda )A=Ak+A\lambda$ ;
$k(\lambda A)=\lambda kA=\lambda (kA)$ .

Определение 11. Матрица B, у которой все элементы равны элементам матрицы A по абсолютной величине, но имеют противоположные знаки по сравнению со знаками соответствующих элементов матрицы A, называется противоположной матрице A и записывается B=(-1)(a_ij).

Заметим, что умножение любой матрицы на нулевую дает в результате нулевую матрицу, как и в обычной алгебре, т.е. 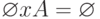$\varnothing xA=\varnothing$ .

Если A - квадратная матрица, то тогда также очевидно равенство

$det(\lambda A)=\lambda ^{n}detA ,$

где n - размер матрицы A.

Определение 12. Если A=(a_ij)_mxp, а B=(b_ij)_pxn, то произведением матрицы A на матрицу B назовем матрицу C, каждый элемент которой вычисляют по формуле:

C = AxB = (a_ij)_mxpx(b_ij)_pxn=(a_s1b_1k+a_s2b_2k+...+a_skb_sk)_mxn=(c_ij)_mxn

Из определения 12 видно, что каждый элемент матрицы C = AB, расположенный в s -ой строке и k -ом столбце равен сумме произведений элементов s -ой строки матрицы A на элементы k -го столбца матрицы B.

При перемножении матриц можно воспользоваться следующей таблицей. Покажем это на примере.

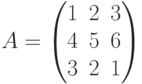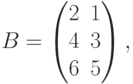Пусть требуется перемножить матрицы $A=\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 3 & 2 & 1 \\ \end{pmatrix}$ и $B=\begin{pmatrix} 2 & 1\\ 4 & 3 \\ 6 & 5 \\ \end{pmatrix},$ т.е. найти AB . Составим таблицу: слева запишем элементы матрицы А (которую умножают), а снизу – элементы матрицы В (на которую умножают):

1	2	3
4	5	6
3	2	1
			2	1
			4	3
			6	5

Результат будем записывать в выделенных ячейках, по формуле – сумма произведений соответствующих элементов:

1	2	3	1x2+2x4+3x6	1x1+2x3+3x5
4	5	6	4x2+5x4+6x6	4x1+5x3+6x5
3	2	1	3x2+2x4+1x6	3x1+2x3+1x5
			2	1
			4	3
			6	5

Произведя вычисления, получаем:

1	2	3	28	22
4	5	6	64	49
3	2	1	20	14
			2	1
			4	3
			6	5

Это и будет искомая матрица (в выделенных ячейках). Это способ очень наглядный и удобный, позволяет избежать ошибок при перемножении матриц.

Известны следующие очевидные свойства произведений матриц

Переместительный закон не выполняется, т.е. 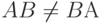$AB \ne BА$ . Поэтому различают умножение на матрицу слева или справа;
(A+B)C=AC+BC
(AB)C=A(BC)=ABC

Определение 13. Если AB = BA, то такие матрицы A и B называют перестановочными или коммутативными.

Очевидно, что коммутативной с единичной будет любая матрица подходящего размера AE = EA = A.

Теорема. Определитель произведения двух квадратных матриц равен произведению определителей этих матриц, т.е. det(AB) = detAxdetB.

Определение 14. Если в некоторой матрице A поменять местами столбцы и строки, то полученная матрица будет называться транспонированной и обозначается A_т.

Определение 15. Если выполняется равенство A = A_т, то такая матрица называется симметрической.

Определение 16. Обратной по отношению к матрице A называется такая матрица, для которой выполняется равенство AA^-1 = A^-1A = E.

Определение 17. Матрица, которая имеет обратную называется обратимой или не особенной.

Теорема. Для того, чтобы матрица A имела обратную матрицу A^-1 необходимо и достаточно, чтобы она была бы невырожденной, т.е. $detA \ne 0$ .

Доказательство. Необходимость. Пусть существует матрица A^-1, тогда

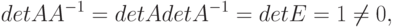
$detAA^{-1} = detAdetA^{-1} = detE = 1 \ne 0 ,$

т.е. ни один из сомножителей не должен быть равен нулю, следовательно, $detA \ne 0$ .

Достаточность. Пусть $detA \ne 0$ . Надо доказать, что существует обратная матрица A^-1. Покажем это на примере квадратной матрицы третьего порядка. Пусть дана матрица

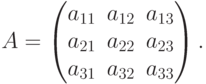
$A= \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}.$

Найдем миноры второго порядка этой матрицы. Очевидно, что таких миноров будет 9: A_is = (-1)^i+s M_is. Составим присоединенную матрицу из полученных алгебраических дополнений, которая обычно обозначается как

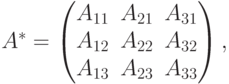
$A^*= \begin{pmatrix} A_{11} & A_{21} & A_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33} \end{pmatrix},$

затем найдем произведение

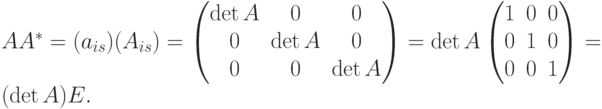
$AA^*=(a_{is})(A_{is})= \begin{pmatrix} \det A & 0 & 0 \\ 0 & \det A & 0 \\ 0 & 0 & \det A \end{pmatrix} = \det A \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} =(\det A)E.$

Т.е. AA^*=(detA)E, следовательно $E=A\frac{1}{\det A}A^*$ , откуда по определению обратной матрицы получаем

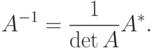$A^{-1}=\frac{1}{\det A}A^*.$

( 2.2)

Теорема доказана. Заметим, что формула (2) известна как популярная расчетная формула для получения обратной матрицы.

Эта важная теорема дает нам простой алгоритм вычисления обратной матрицы, который можно сформулировать так.

Вычислить detA ;^{1Этот пункт является обязательным в данном алгоритме. При равенстве нулю детерминанта делается вывод о том, что обратной матрицы не существует и решение не продолжается. Если детерминант отличен от нуля, то обратная матрица существует и может быть найдена по указанной схеме.}
Вычислить все алгебраические дополнения матрицы A ;
Найти обратную матрицу по формуле 2.

Пример. Найти обратную матрицу для 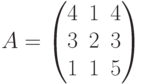$A= \begin{pmatrix} 4 & 1 & 4 \\ 3 & 2 & 3 \\ 1 & 1 & 5 \end{pmatrix}$ и выполнить проверку.

Решение. Вычисляем

$\det A = \begin{vmatrix} 4 & 1 & 4 \\ 3 & 2 & 3 \\ 1 & 1 & 5 \end{vmatrix} =20 \ne 0,$

следовательно, обратная матрица существует. Найдем присоединенную матрицу A^*. Для этого вычислим все миноры второго порядка матрицы A и алгебраические дополнения:

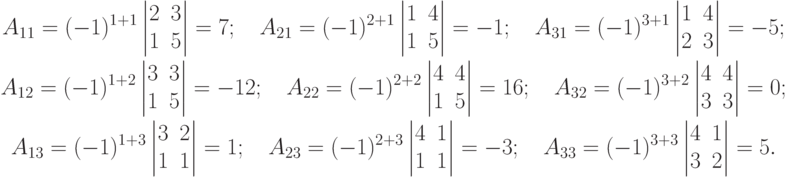
$\begin{gathered} A_{11}=(-1)^{1+1} \begin{vmatrix} 2 & 3 \\ 1 & 5 \end{vmatrix} =7; \quad A_{21}=(-1)^{2+1} \begin{vmatrix} 1 & 4 \\ 1 & 5 \end{vmatrix} =-1; \quad A_{31}=(-1)^{3+1} \begin{vmatrix} 1 & 4 \\ 2 & 3 \end{vmatrix} =-5; \\ A_{12}=(-1)^{1+2} \begin{vmatrix} 3 & 3 \\ 1 & 5 \end{vmatrix} =-12; \quad A_{22}=(-1)^{2+2} \begin{vmatrix} 4 & 4 \\ 1 & 5 \end{vmatrix} =16; \quad A_{32}=(-1)^{3+2} \begin{vmatrix} 4 & 4 \\ 3 & 3 \end{vmatrix} =0; \\ A_{13}=(-1)^{1+3} \begin{vmatrix} 3 & 2 \\ 1 & 1 \end{vmatrix} =1; \quad A_{23}=(-1)^{2+3} \begin{vmatrix} 4 & 1 \\ 1 & 1 \end{vmatrix} =-3; \quad A_{33}=(-1)^{3+3} \begin{vmatrix} 4 & 1 \\ 3 & 2 \end{vmatrix} =5. \end{gathered}$

Составим

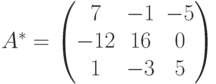
$A^*= \begin{pmatrix} 7 & -1 & -5 \\ -12 & 16 & 0 \\ 1 & -3 & 5 \end{pmatrix}$

и найдем по формуле (2) обратную матрицу:

$A^{-1}=\frac{1}{20} \begin{pmatrix} 7 & -1 & -5 \\ -12 & 16 & 0 \\ 1 & -3 & 5 \end{pmatrix}$

Проверка

$AA^{-1}= \begin{pmatrix} 4 & 1 & 4 \\ 3 & 2 & 3 \\ 1 & 1 & 5 \end{pmatrix} \frac{1}{20} \begin{pmatrix} 7 & -1 & -5 \\ -12 & 16 & 0 \\ 1 & -3 & 5 \end{pmatrix} =\frac{1}{20} \begin{pmatrix} 20 & 0 & 0 \\ 0 & 20 & 0 \\ 0 & 0 & 20 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}.$

Дальше >>

Авторизоваться

Введение в линейную алгебру

Матрицы. Основные определения и виды матриц. Действия над матрицами. Понятие ранга матрицы. Операции над матрицами. Понятие и нахождение обратной матрицы

Операции над матрицами

Вопросы и ответы