|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Интегрирование логарифмических и экспоненциальных функций. Решение дифференциального уравнения Риша
Решение дифференциального уравнения Риша
27.1. ТЕОРЕМА (Риш).
Пусть  . Тогда можно за конечное число шагов
найти элементы
. Тогда можно за конечное число шагов
найти элементы  и систему линейных
уравнений
и систему линейных
уравнений  от
от  неизвестных с коэффициентами в
поле
неизвестных с коэффициентами в
поле  , такие, что уравнение
, такие, что уравнение
 |
( 27.1) |
 и
и 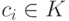 тогда и только
тогда, когда
тогда и только
тогда, когда  , где
, где  и константы
и константы 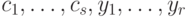 удовлетворяют системе
удовлетворяют системе  .
.ДОКАЗАТЕЛЬСТВО. Основание индукции: 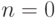 ,
,  .
.
Доказательство теоремы в этом случае проведем в два этапа: сначала избавляемся от знаменателей, затем решаем полиномиальное уравнение.
Этап 1.
Пусть  удовлетворяет уравнению (27.1). Мы можем записать
удовлетворяет уравнению (27.1). Мы можем записать  ,
и пусть
,
и пусть 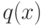 - неприводимый в кольце
- неприводимый в кольце ![K[x]](/sites/default/files/tex_cache/a77a9131b3530308247cff0e3c92321a.png) многочлен со старшим коэффициентом равным 1, делящий
многочлен со старшим коэффициентом равным 1, делящий 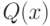 . Предположим, что
. Предположим, что  делит
делит 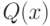 , а
, а  не
делит
не
делит 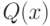 . Воспользуемся техникой
. Воспользуемся техникой  -адических
расширений и запишем
-адических
расширений и запишем
 |
( 27.2) |
![A, B, C\in K[x]](/sites/default/files/tex_cache/78236e96eb2bbb8e3bdda93a03a0aba4.png) ,
,  ,
,  ,
,  , а
точками обозначены
слагаемые, имеющие в знаменателе
, а
точками обозначены
слагаемые, имеющие в знаменателе  в меньшей степени, чем главный
член (эти слагаемые могут также включать степенной ряд).
Заметим, что
в меньшей степени, чем главный
член (эти слагаемые могут также включать степенной ряд).
Заметим, что  и
и  нам известны, т.\;к. известна
функция
нам известны, т.\;к. известна
функция  , а также нам известно ограничение на
, а также нам известно ограничение на  сверху (максимальное
значение
сверху (максимальное
значение  соответствующего показателя для
функций
соответствующего показателя для
функций  ). Поскольку
). Поскольку  могут принимать любые
значения,
могут принимать любые
значения,  может не
совпадать с
может не
совпадать с  . Подставляя выражения (27.2) в уравнение (27.1), получим
. Подставляя выражения (27.2) в уравнение (27.1), получим |
( 27.3) |
 является неприводимым, следовательно, выписанные
слагаемые не допускают сокращения числителя и знаменателя (
является неприводимым, следовательно, выписанные
слагаемые не допускают сокращения числителя и знаменателя (  не
делит ни
не
делит ни 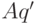 , ни
, ни 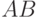 ). Выделяя главный член
разложения по
). Выделяя главный член
разложения по  , получим или
, получим или
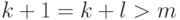 . Последняя возможность встречается только в том
случае, когда два старших члена в соотношении (27.3) взаимно
сократятся, т. е.
. Последняя возможность встречается только в том
случае, когда два старших члена в соотношении (27.3) взаимно
сократятся, т. е.  делит
делит  , следовательно,
, следовательно,  делит
делит 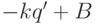 , а так как
, а так как  и
и  , то
, то  , т. е.
, т. е.  . Таким образом, число
. Таким образом, число  ограничено сверху числом
ограничено сверху числом  , где
, где  появляется только
в том случае, если оно является целым числом. Мы получили вычислимую границу
для
появляется только
в том случае, если оно является целым числом. Мы получили вычислимую границу
для  и можем в уравнении
(27.1) перейти к новой неизвестной
функции
и можем в уравнении
(27.1) перейти к новой неизвестной
функции  , знаменатель которой не делится на
, знаменатель которой не делится на  .
.Заметим, что множитель  может появиться в
может появиться в  только в том случае, если на
только в том случае, если на  делится знаменатель хотя бы одного
из элементов
делится знаменатель хотя бы одного
из элементов  . Действительно, в противном случае
. Действительно, в противном случае  и если
и если  , то слагаемое
, то слагаемое  не может ни с чем
сократиться. Таким образом, у нас имеется только конечное число неприводимых
сомножителей
не может ни с чем
сократиться. Таким образом, у нас имеется только конечное число неприводимых
сомножителей  , которые могут появляться в
знаменателе элемента
, которые могут появляться в
знаменателе элемента  , и степени этих сомножителей ограничены
вычисляемыми константами
, и степени этих сомножителей ограничены
вычисляемыми константами 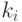 . Положим
. Положим  . Тогда
. Тогда  является многочленом (для любого
решения
является многочленом (для любого
решения  исходного уравнения).
исходного уравнения).
После подстановки  в уравнение (27.1) и умножения получившегося уравнения на
в уравнение (27.1) и умножения получившегося уравнения на  ,
получаем уравнение вида
,
получаем уравнение вида
 |
( 27.4) |
![R,V,T_i\in K[x]](/sites/default/files/tex_cache/53d0e66567a17a88791556e4ef3b7a06.png) и не зависят от
и не зависят от  ,
которые все еще не определены.
,
которые все еще не определены.Этап 2.
Тот же метод применим для ограничения сверху степени неизвестного многочлена  . Запишем
. Запишем
 |
( 27.5) |
 , а имеем
ограничение
, а имеем
ограничение  . Подставляя
(27.5) в уравнение (27.4), получим
. Подставляя
(27.5) в уравнение (27.4), получим |
( 27.6) |
Сравнивая старшие одночлены в правой и левой частях, снова получаем две возможности:
 |
( 27.7) |
 |
( 27.8) |
 , а именно,
, а именно, |
( 27.9) |
 . Раскрывая скобки и приравнивая коэффициенты при
одинаковых степенях переменной
. Раскрывая скобки и приравнивая коэффициенты при
одинаковых степенях переменной  в уравнении (27.6), получаем требуемую систему
в уравнении (27.6), получаем требуемую систему  линейных уравнений.
линейных уравнений.Шаг индукции: Предположим, теорема доказана для дифференциального
поля  , и докажем
ее для дифференциального поля
, и докажем
ее для дифференциального поля  , где для
упрощения записи мы будем использовать обозначение
, где для
упрощения записи мы будем использовать обозначение  .
Случаи, когда
.
Случаи, когда  является логарифмом и экспонентой, будем
рассматривать раздельно.
является логарифмом и экспонентой, будем
рассматривать раздельно.
Случай 1.  .
.
Доказательство следует тем же путем, что и при 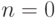 .
.
Этап 1 проходит практически без изменений. Отметим только, что без потери
общности мы можем считать многочлен  нормированным,
т. е. его старший коэффициент равен 1. В этом случае
нормированным,
т. е. его старший коэффициент равен 1. В этом случае  (мы рассматриваем операцию дифференцирования в
дифференциальном поле
(мы рассматриваем операцию дифференцирования в
дифференциальном поле  , т. е.
, т. е. 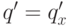 , если
, если  - некоторое поле функций, а степени многочленов
рассматриваем
относительно переменной
- некоторое поле функций, а степени многочленов
рассматриваем
относительно переменной  ).
).
Логика этапа 2 остается такой же, но уравнение (27.6) принимает теперь вид
 |
( 27.10) |
Здесь нужно рассматривать отдельно два подслучая:  и
и 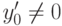 . Как и прежде, пусть
. Как и прежде, пусть 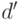 обозначает верхнюю
границу для
обозначает верхнюю
границу для  .
.
Выделяя старшие одночлены в слагаемых и сравнивая их степени, получаем следующие ограничения:
если 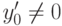 , то либо
, то либо  либо
либо  ;
;
если  , то либо
, то либо  либо
либо  .
.
Как и в случае 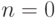 , вторая возможность в обоих случаях требует
более детального рассмотрения.
, вторая возможность в обоих случаях требует
более детального рассмотрения.
Подслучай 1 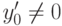 . Неравенство
. Неравенство  может иметь место только тогда, когда
может иметь место только тогда, когда

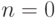 мы приравниваем нулю два
старших коэффициента, поскольку
старший коэффициент не зависит от
мы приравниваем нулю два
старших коэффициента, поскольку
старший коэффициент не зависит от  . Соответственно, этим же
объясняется замена неравенства
. Соответственно, этим же
объясняется замена неравенства  на
на  .)
.)Второе уравнение можно переписать в виде

 , переписываем это уравнение в виде
, переписываем это уравнение в виде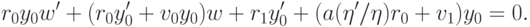
 из первого уравнения, получаем
из первого уравнения, получаем

 , и по предположению индукции мы можем его
проинтегрировать. Согласно принципа Лиувилля результат интегрирования
(определенный с точностью до аддитивной константы)
представляется в виде суммы рациональной функции (из поля
, и по предположению индукции мы можем его
проинтегрировать. Согласно принципа Лиувилля результат интегрирования
(определенный с точностью до аддитивной константы)
представляется в виде суммы рациональной функции (из поля  , а
точнее его конечного расширения, получаемого присоединением
конечного числа алгебраических над
, а
точнее его конечного расширения, получаемого присоединением
конечного числа алгебраических над  констант) и логарифмической
части. Эта логарифмическая часть определена однозначно, и если
ее нельзя представить в виде
констант) и логарифмической
части. Эта логарифмическая часть определена однозначно, и если
ее нельзя представить в виде  , где
, где  -
целое положительное число, то старший член решения уравнения
-
целое положительное число, то старший член решения уравнения |
( 27.11) |
![R,V,T_i\in \EuScript D[\theta]](/sites/default/files/tex_cache/48c3101d3fe2cfecde10023a787423ce.png) и не зависят от
и не зависят от  , не
может иметь вид
, не
может иметь вид 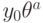 , где
, где 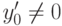 и
и  удовлетворяет
неравенству
удовлетворяет
неравенству  .
.Подслучай 2  . Неравенство
. Неравенство  может иметь место только тогда, когда
может иметь место только тогда, когда

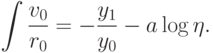
 . Заметим, что в
этом случае мы снова воспользовались предположением индукции
для выполнения операции интегрирования. Отметим также, что для каждого
конкретного уравнения вида (27.11) нужно
рассматривать
не более одного интеграла, в зависимости от того, какое условие
. Заметим, что в
этом случае мы снова воспользовались предположением индукции
для выполнения операции интегрирования. Отметим также, что для каждого
конкретного уравнения вида (27.11) нужно
рассматривать
не более одного интеграла, в зависимости от того, какое условие  или
или 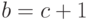 имеет место; если ни одно из этих
равенств не
выполняется, то
имеет место; если ни одно из этих
равенств не
выполняется, то  .
.Окончание доказательства этапа 2 ничем не отличается от случая 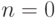 .
.
Случай 2.  , т. е.
, т. е. 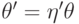 .
.
В этом случае при дифференцировании степень многочлена от  не понижается, поэтому доказательство этапа 1, проведенное
выше, дословно не проходит (там существенно используется, что
не понижается, поэтому доказательство этапа 1, проведенное
выше, дословно не проходит (там существенно используется, что  ). В данном случае нужно вместо
). В данном случае нужно вместо 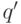 рассматривать
остаток от деления
рассматривать
остаток от деления 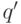 на
на  , т. е. такой многочлен
, т. е. такой многочлен  , что
, что  и
и  . Случай
. Случай 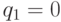 соответствует тому, что
соответствует тому, что  , где
, где  .
Следовательно,
.
Следовательно,  равняется отношению старших коэффициентов
многочленов
равняется отношению старших коэффициентов
многочленов 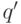 и
и  . Поскольку мы предполагаем, что
старший коэффициент многочлена
. Поскольку мы предполагаем, что
старший коэффициент многочлена  равен 1,
равен 1,  равно старшему
коэффициенту многочлена
равно старшему
коэффициенту многочлена 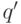 , который равен
, который равен 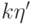 ,
где
,
где  степень многочлена
степень многочлена  (и
(и 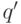 ).
Решение дифференциального уравнения
).
Решение дифференциального уравнения  определено с точностью до мультипликативной константы
и имеет вид
определено с точностью до мультипликативной константы
и имеет вид  . Из условия
нормированности следует, что
. Из условия
нормированности следует, что 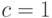 , а из неприводимости
, а из неприводимости  следует, что
следует, что 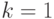 .
.
Для неприводимых многочленов  отличных от
отличных от  этап 1 проходит с заменой
этап 1 проходит с заменой 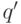 на
на  , поскольку
единственное место, где
мы по-существу пользовались тем, что
, поскольку
единственное место, где
мы по-существу пользовались тем, что 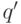 - ненулевой
многочлен, степень которого меньше степени
- ненулевой
многочлен, степень которого меньше степени  , это уравнение
(27.3), главный член первого слагамого в котором теперь принимает вид
, это уравнение
(27.3), главный член первого слагамого в котором теперь принимает вид 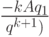 , главный член первого
слагамого в котором теперь принимает
вид
, главный член первого
слагамого в котором теперь принимает
вид  .
.
Таким образом, на этапе 2 нам нужно рассматривать обобщенные многочлены,
т. е. выражения вида  и
ограничивать их степени сверху и снизу. Вычисления для верхней и нижней оценок
абсолютно аналогичны. Заметим, что дифференцируя
одночлен
и
ограничивать их степени сверху и снизу. Вычисления для верхней и нижней оценок
абсолютно аналогичны. Заметим, что дифференцируя
одночлен  , мы получаем одночлен той же степени
(
, мы получаем одночлен той же степени
(  ), при этом нулевой результат может получиться только
при
), при этом нулевой результат может получиться только
при  ,
поскольку
,
поскольку  и решение
дифференциального уравнения
и решение
дифференциального уравнения  имеет
вид
имеет
вид 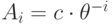 , что при
, что при  не принадлежит
полю
не принадлежит
полю  .
.
Детали доказательства оставляются читателю в качестве упражнения.
