|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Проблема представления данных
Кольца вычетов и конечные поля.
Кольца вычетов и конечные поля представляют собой наиболее простые объекты с точки зрения задачи представления данных. Каждому элементу такого
кольца или поля, состоящего из n элементов, можно сопоставить,
например, взаимно однозначно неотрицательное целое число из отрезка [0, n - 1]. Для колец вычетов — это сопоставление каждому
классу вычетов его единственного элемента, лежащего в [0, n - 1],
при этом арифметические операции над такими "числами" выполняются как операции над целыми числами по модулю n. Часто в
качестве системы представителей кольца вычетов 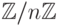 выбирается отрезок [-(n-1)/2, (n-1)/2] при нечетном n и [-n/2+1, n/2] при
четном n. Арифметические операции +, -, * реализуются очевидным образом, для реализации операции деления обычно используется расширенный алгоритм Евклида (см.
"Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация"
).
выбирается отрезок [-(n-1)/2, (n-1)/2] при нечетном n и [-n/2+1, n/2] при
четном n. Арифметические операции +, -, * реализуются очевидным образом, для реализации операции деления обычно используется расширенный алгоритм Евклида (см.
"Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация"
).
Хотя элементы конечного поля из n элементов также находятся
во взаимнооднозначном соответствии с целыми числами из отрезка [0, n - 1], это соответствие не является таким же естественным, в
частности, арифметические операции выполняются по более сложным правилам. Чаще используются другие формы представления,
например, для записи элементов простого поля из p элементов ис
пользуется система вычетов по модулю p, а поле GF(pk) представляется в виде факторкольца кольца многочленов ![\mathbb Zp[x]](/sites/default/files/tex_cache/cdb150597e19633d8f122edeb86ff148.png) по идеалу,
порожденному некоторым неприводимым по модулю p многочленом
степени k.
по идеалу,
порожденному некоторым неприводимым по модулю p многочленом
степени k.
Сформулируем основные результаты о конечных полях.
- Любая конечная область целостности является полем (следует из взаимной однозначности умножения на любой ненулевой элемент).
- Характеристика конечного поля является простым числом (следует из отсутствия делителей нуля).
- Любое конечное поле GF(q) характеристики p состоит из q = pk элементов, где k — натуральное число (поскольку
оно является векторным пространством над
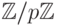 , k — размерность этого пространства).
, k — размерность этого пространства). - Мультипликативный порядок любого ненулевого элемента поля GF(q) делит q - 1 (ненулевые элементы образуют по умножению группу порядка q - 1 ).
- Мультипликативная группа поля GF(q) является циклической, т. е. существует элемент порядка q-1 (следует из однозначности разложения на множители многочленов xm-1 над любым полем).
- Любые два конечных поля, содержащих одинаковое число элементов, изоморфны (следует из однозначности поля разложения для многочлена xq-1 - 1 ).
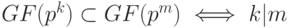
Таким образом, существует два принципиально разных подхода к построению канонического представления элементов конечного поля GF(pk):
- (векторное представление) выбрать элемент x такой, что
его степени x0 = 1, x, x2, . . . , xk-1 порождают наше поле
как векторное пространство над простым подполем
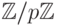 ,
и любой элемент записывать как вектор в этом базисе;
,
и любой элемент записывать как вектор в этом базисе; - (степенное представление) найти примитивный элемент
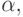 порождающий мультипликативную группу этого поля, и любой элемент поля представлять в виде степени элемента
порождающий мультипликативную группу этого поля, и любой элемент поля представлять в виде степени элемента 
Отметим, что переход от степенного представления к векторному достаточно прост, а обратный переход (вычисление дискретного логарифма) — очень сложен. Сложность этой задачи используется в криптографии для построения систем кодирования с открытым ключом.
1.4. УПРАЖНЕНИЯ.
- Показать, что кольцо вычетов по модулю p2 не изоморфно конечному полю из p2 элементов.
- Составить таблицу умножения и деления для колец
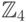 и
и 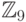 и для полей GF(4) и GF(9).
и для полей GF(4) и GF(9). - Для заданной матрицы размера p2 x p2, где p = 2 или 3, проверить, является ли она таблицей умножения в поле GF(p2) при какой-либо нумерации элементов этого поля.
- Реализовать алгоритм деления в кольце вычетов
 (учесть
возможность получения неоднозначного результата).
(учесть
возможность получения неоднозначного результата). -
Китайская теорема об остатках. Дано k взаимно простых
натуральных чисел mi > 1. Для любого набора из k целых
чисел ai, 1 <= i <= k, найти
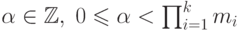 , такое,
что
, такое,
что  для всех i от 1 до k.
для всех i от 1 до k. - Обобщить предыдущую задачу на случай, когда числа mi не обязательно взаимно просты.
- Найти все неприводимые над полем
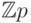 многочлены степени n ( n небольшое).
многочлены степени n ( n небольшое). - Найти число неприводимых над полем
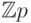 многочленов степени n.
многочленов степени n.
Рациональные числа.
Множество рациональных чисел  определяется как фактормножество множества пар
определяется как фактормножество множества пар 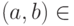
 x
x  ,
,  , по отношению эквивалентности:
, по отношению эквивалентности:  .
Если у нас фиксирована каноническая форма целого числа, то каноническую форму рационального числа мы можем получить, например, выбирая из эквивалентных пар целых чисел (a, b) такую, у
которой b > 0 и НОД(a, b) = 1. Все сказанное выше о представлении
целых чисел относится и к представлению рациональных чисел.
.
Если у нас фиксирована каноническая форма целого числа, то каноническую форму рационального числа мы можем получить, например, выбирая из эквивалентных пар целых чисел (a, b) такую, у
которой b > 0 и НОД(a, b) = 1. Все сказанное выше о представлении
целых чисел относится и к представлению рациональных чисел.
Естественно, приведенная выше каноническая форма рационального числа не является единственно возможной. Из школьного курса известно, что любое рациональное число можно представить в виде бесконечной десятичной периодической дроби. Также известно, что любая бесконечная периодическая дробь представляет рациональное число, причем соответствие между рациональными дробями и бесконечными десятичными периодическими дробями не является взаимно однозначным: рациональные числа, знаменатели которых имеют вид 2n5m, могут быть представлены периодическими дробями с периодами (0) и (9).
1.5. УПРАЖНЕНИЯ. Пусть m — натуральное число, m > 1, рассматриваемое как основание системы счисления.
- Доказать, что рациональные числа могут быть представлены бесконечными периодическими m -ичными дробями, причем неоднозначно.
- Доказать, что любая бесконечная периодическая m -ичная дробь представляет некоторое рациональное число.
- Установить взаимнооднозначное соответствие между множеством рациональных дробей и некоторым подмножеством бесконечных периодических m -ичных дробей.
- Написать программу перевода рациональных чисел в бесконечные периодические m -ичные дроби и обратно.
Часто рациональные числа представляют в виде суммы целого
числа и правильной дроби, т. е. положительного рационального числа 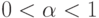 . Исследователи утверждают, что в древнем Египте
имелись обозначения только для дробей с числителем 1, остальные
числа представлялись в виде суммы таких дробей.
. Исследователи утверждают, что в древнем Египте
имелись обозначения только для дробей с числителем 1, остальные
числа представлялись в виде суммы таких дробей.
1.6. УПРАЖНЕНИЯ.
- Доказать, что любое положительное рациональное число
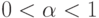 можно представить в виде суммы обратных величин различных натуральных чисел.
можно представить в виде суммы обратных величин различных натуральных чисел. - Показать, что такое представление не единственно.
- Описать алгоритм, выбирающий из всех возможных представлений такого вида единственное.
- Написать программу, представляющую любое положительное рациональное число
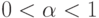 в виде суммы обратных
величин различных натуральных чисел.
в виде суммы обратных
величин различных натуральных чисел.
