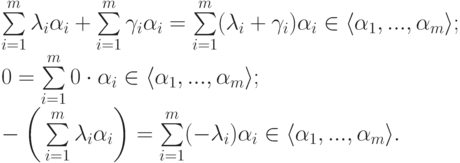НОУ ИНТУИТ | Введение в алгебру. Лекция 9: Линейное пространство строк над полем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5319 / 590 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

Теги: beta, алгебра, алгоритмы, гомоморфизм групп, гомоморфизм группоидов, группоид, изоморфизм группоидов, инъекция, коэффициентами системы, моноид, полугруппа, расширенная матрица, старший коэффициент, элементы

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматривается линейное пространство строк над полем. Приведены определения возможных операций над строками, рассмотрен ряд характерных задач, доказаны основные теоремы, а также приведены задачи для самостоятельного рассмотрения

Ключевые слова: коэффициентами системы, расширенная матрица, поле, операции, сложение строк, линейное пространство над полем, линейная оболочка строк

Линейное пространство строк над полем

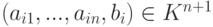Систематическое рассмотрение строки коэффициентов $(a_{i1},...,a_{in})\in K^n$ i -го уравнения a_i1x₁+...+a_inx_n=b_i ( i -я строка матрицы A=(a_ij) коэффициентов системы линейных уравнений), строки $(a_{i1},...,a_{in},b_i)\in K^{n+1}$ всех коэффициентов i -го уравнения (включая свободный член b_i i -й строки расширенной матрицы A=(a_ij,b_i) системы линейных уравнений), строки 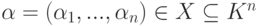$\alpha=(\alpha_1,...,\alpha_n)\in X\subseteq K^n$ , являющейся решением системы линейных уравнений, с операциями сложения и умножения на элементы из поля K естественно подвело нас к определению линейного пространства строк Kⁿ.

Пусть K - поле (например, K= R - поле действительных чисел). Рассмотрим

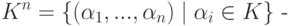
$K^n= \{(\alpha_1,...,\alpha_n)\mid \alpha_i\in K\} \text{ -}$

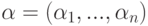совокупность всех упорядоченных строк $\alpha=(\alpha_1,...,\alpha_n)$ длины n элементов 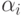$\alpha_i$ , i=1,...,n, поля K. На множестве Kⁿ определены следующие операции.

Сложение строк (бинарная операция):если
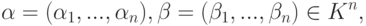
$\alpha=(\alpha_1,...,\alpha_n),\beta=(\beta_1,...,\beta_n)\in K^n,$
то
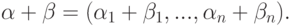
$\alpha+\beta=(\alpha_1+\beta_1,...,\alpha_n+\beta_n).$
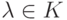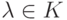Для каждого элемента $\lambda\in K$ (унарная) операция умножение строк на элемент $\lambda\in K$ }: если
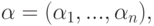
$\alpha=(\alpha_1,...,\alpha_n),$
то
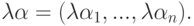
$\lambda\alpha=(\lambda\alpha_1,...,\lambda\alpha_n).$

Свойства операций

(1.1) Ассоциативность сложения строк: если 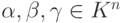$\alpha,\beta,\gamma\in K^n$ , то $(\alpha+\beta)+\gamma=\alpha+(\beta+\gamma)$ .

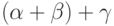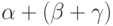Действительно, на i -м месте в $(\alpha+\beta)+\gamma$ и в $\alpha+(\beta+\gamma)$ имеем $(\alpha_i+\beta_i)+\gamma_i=\alpha_i+(\beta_i+\gamma_i)$ (ассоциативность сложения в поле K ).

(1.2) Коммутативность сложения строк: если 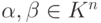$\alpha,\beta\in K^n$ , то $\alpha+\beta=\beta+\alpha$ .

Действительно, на i -м месте в $\alpha+\beta$ и в $\beta+\alpha$ имеем $\alpha_i+\beta_i=\beta_i+\alpha_i$ (коммутативность сложения в поле K ).

(1.3) Нулевая строка (0,...,0) в Kⁿ является нейтральным элементом для операции сложения в Kⁿ, поскольку 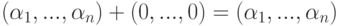$(\alpha_1,...,\alpha_n)+(0,...,0)=(\alpha_1,...,\alpha_n)$ для любой строки $(\alpha_1,...,\alpha_n)\in K^n$ .

(1.4) Для любой строки 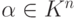$\alpha\in K^n$ существует противоположная строка $\delta$ такая, что $\alpha+\delta=(0,...,0)$ .

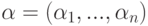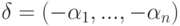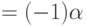Действительно, если $\alpha=(\alpha_1,...,\alpha_n)$ , то для $\delta=(-\alpha_1,...,-\alpha_n)$ ( ${}=(-1)\alpha$ ) имеем $\alpha+\delta=(0,...,0)$ .

Таким образом, свойства (1.1)-(1.4) означают, что множество строк Kⁿ с операцией сложения строк является коммутативной группой.

(2.1) Если 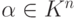$1\in K$ , $\alpha\in K^n$ , то $1\cdot\alpha=\alpha$ .

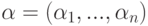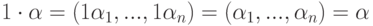Действительно, для $\alpha=(\alpha_1,...,\alpha_n)$ имеем $1\cdot\alpha=(1\alpha_1,...,1\alpha_n)=(\alpha_1,...,\alpha_n)= \alpha$ .

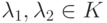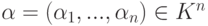(2.2) Если $\lambda_1,\lambda_2\in K$ , $\alpha=(\alpha_1,...,\alpha_n)\in K^n$ , то $\lambda_1(\lambda_2\alpha)=(\lambda_1\lambda_2)\alpha$ .

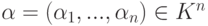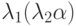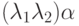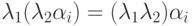Действительно, для $\alpha=(\alpha_1,...,\alpha_n)\in K^n$ на i -м месте в $\lambda_1(\lambda_2\alpha)$ и в $(\lambda_1\lambda_2)\alpha$ имеем $\lambda_1(\lambda_2\alpha_i)=(\lambda_1\lambda_2)\alpha_i$ (ассоциативность умножения в поле K ).

(3.1) Если 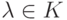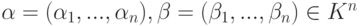$\lambda\in K$ , $\alpha=(\alpha_1,...,\alpha_n), \beta=(\beta_1,...,\beta_n)\in K^n$ , то $\lambda(\alpha+\beta)=\lambda\alpha+\lambda\beta$ .

Действительно, на i -м месте в 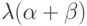$\lambda(\alpha+\beta)$ и в $\lambda\alpha+\lambda\beta$ имеем $\lambda(\alpha_i+\beta_i)=\lambda\alpha_i+\lambda\beta_i$ (дистрибутивность в поле K ).

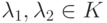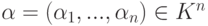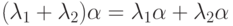(3.2) Если $\lambda_1,\lambda_2\in K$ , $\alpha=(\alpha_1,...,\alpha_n)\in K^n$ , то $(\lambda_1+\lambda_2)\alpha=\lambda_1\alpha+\lambda_2\alpha$ .

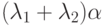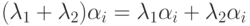Действительно, на i -м месте в $(\lambda_1+\lambda_2)\alpha$ и в $\lambda_1\alpha+\lambda_2\alpha$ имеем $(\lambda_1+\lambda_2)\alpha_i=\lambda_1\alpha_i+\lambda_2\alpha_i$ (дистрибутивность в поле K ).

Определение 4.1.1. Множество V с операцией сложения и операциями умножения на элементы $\lambda$ поля K, удовлетворяющее свойствам (1.1)-(1.4), (2.1), (2.2), (3.1), (3.2), называется линейным пространством над полем K .

Итогом наших проверок является

Теорема 4.1.2. Множество Kⁿ строк длины n элементов поля K с операцией сложения и с операциями умножения на элементы $\lambda$ поля K является линейным пространством над полем K.

Определение 4.1.3. Если

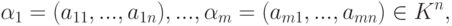
$\alpha_1=(a_{11},...,a_{1n}),...,\alpha_m=(a_{m1},...,a_{mn}) \in K^n,$

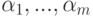
то совокупность всех линейных комбинаций строк $\alpha_1,...,\alpha_m$

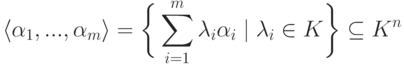
$\langle \alpha_1,...,\alpha_m\rangle= \biggl\{\,\sum\limits_{i=1}^{m}\lambda_i\alpha_i\mid \lambda_i\in K\biggr\}\subseteq K^n$

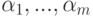называется линейной оболочкой строк $\alpha_1,...,\alpha_m$ .

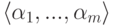Лемма 4.1.4. Если $\alpha_1,...,\alpha_m\in K^n$ , то линейная оболочка $\langle \alpha_1,...,\alpha_m\rangle$ является линейным пространством (подпространством в линейном пространстве строк Kⁿ ).

Доказательство. Для 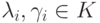$\lambda_i,\gamma_i\in K$ имеем:

$\begin{gathe} \sum\limits_{i=1}^{m}\lambda_i\alpha_i+ \sum\limits_{i=1}^{m}\gamma_i\alpha_i= \sum\limits_{i=1}^{m}(\lambda_i+\gamma_i)\alpha_i\in \langle \alpha_1,...,\alpha_m\rangle; \\ 0=\sum\limits_{i=1}^{m}0\cdot \alpha_i\in \langle \alpha_1,...,\alpha_m\rangle; \\ -\biggl(\,\sum\limits_{i=1}^{m}\lambda_i\alpha_i\biggr)= \sum\limits_{i=1}^{m}(-\lambda_i)\alpha_i\in \langle \alpha_1,...,\alpha_m\rangle. \end{gathe}$

Дальше >>

Авторизоваться

Введение в алгебру

Линейное пространство строк над полем

Линейное пространство строк над полем

Свойства операций

Вопросы и ответы