НОУ ИНТУИТ | Введение в алгебру. Лекция 3: Кольца. Поля. Идеалы и гомоморфизмы колец

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5310 / 589 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

Теги: beta, алгебра, алгоритмы, гомоморфизм групп, гомоморфизм группоидов, группоид, изоморфизм группоидов, инъекция, коэффициентами системы, моноид, полугруппа, расширенная матрица, старший коэффициент, элементы

|

Вам нравится? Нравится 68 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются понятия колец. Приведены основные определения и свойства элементов кольца, рассмотрены ассоциативные кольца. Рассмотрен ряд характерных задач, доказаны основные теоремы, а также приведены задачи для самостоятельного рассмотрения

Ключевые слова: кольцо ассоциативное с единицей, коммутативным, группа, корректность, операции, законы ассоциативности, Законы дистрибутивности, подкольцо, элемент нильпотентный, степень нильпотентности элемента, идемпотент, функция Эйлера, поле, доказательство, поле вычетов, простое число, делителем, пересечение, натуральное число, идеал кольца левый, идеал кольца двусторонний, подгруппа, идеал кольца главный, гомоморфизм колец, ядро, изоморфизм колец, отображение

Кольца

Множество R с двумя бинарными операциями (сложением + и умножением $\cdot$ ) называется ассоциативным кольцом с единицей , если:

относительно сложения (R,+) - абелева (т. е. коммутативная) группа;
умножение - ассоциативная операция, и существует нейтральный элемент 1 (т. е. 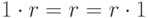$1\cdot r=r=r\cdot 1$ для всех 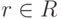$r\in R$ ), называемый единицей;
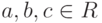сложение и умножение связаны законами дистрибутивности (a+b)c=ac+bc, c(a+b)=ca+cb для всех $a,b,c\in R$ .

Если операция умножения коммутативна, то кольцо 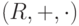$(R,{+},{\cdot})$ называется коммутативным кольцом. Коммутативные кольца являются одним из главных объектов изучения в коммутативной алгебре и алгебраической геометрии.

Замечания 1.10.1.

Исследуются и неассоциативные кольца. Например, если вместо ассоциативности 2) умножение удовлетворяет тождеству Якоби a(bc)+b(ca)+c(ab)=0 для всех 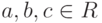$a,b,c\in R$ и ab=-ba для всех $a,b\in R$ , то такое кольцо называется кольцом Ли.
Рассматриваются также и ассоциативные кольца без единицы. Например, четные числа R=2Z являются ассоциативным коммутативным кольцом без единицы.

Примеры 1.10.2 (примеры ассоциативных колец).

Кольцо 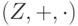$(Z,{+},{\cdot})$ целых чисел; поля Q, R.
Кольцо непрерывных вещественных функций C[0,1] на отрезке [0,1] (для $f,g\in C[0,1]$ , $x\in [0,1]$ : (f+g)(x)=f(x)+g(x), (fg)(x)=f(x)g(x) ).
Кольцо многочленов R[x] с действительными коэффициентами.
Кольцо вычетов 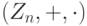$(Z_n,{+},{\cdot})$ по модулю n.

Мы уже убедились, что группа вычетов (Z_n,+)={C₀,C₁,...,C_n-1}, C_k=k+nZ, по модулю n с операцией сложения 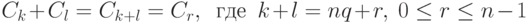$C_k+C_l=C_{k+l}=C_r,\ \ \text{где}\ \ k+l=nq+r,\ 0 \leq r \leq n-1$ , является коммутативной группой (см. пример 1.9.4, 2)).

Определим операцию умножения, полагая 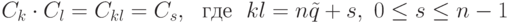$C_k\cdot C_l=C_{kl}=C_s,\ \ \text{где}\ \ kl=n\tilde q+s,\ 0 \leq s \leq n-1$ . Проверим корректность этой операции. Если C_k=C_k', C_l=C_l', то k'=k+nu, l'=l+nv, 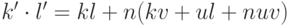$k'\cdot l'=kl+n(kv+ul+nuv)$ , и поэтому C_k'l'=C_kl.

Так как (C_kC_l)C_m=C_(kl)m=C_k(lm)=C_k(C_lC_m), C_kC_l=C_kl=C_lk=C_lC_k, C₁C_k=C_k=C_kC₁, (C_k+C_l)C_m=C_(k+l)m=C_km+lm=C_kC_m+C_lC_m, то $(Z_n,{+},{\cdot})$ является ассоциативным коммутативным кольцом с единицей C₁ кольцом вычетов по модулю n ).

Свойства колец (R,+,.)

Так как (R,+) - абелева группа, то: существует, и единственный, нейтральный элемент относительно сложения 0 ; для любого $a\in R$ существует, и единственный, противоположный элемент -a (т. е. a+(-a)=0 ); уравнение x+b=a имеет, и единственное, решение x=a-b=a+(-b).
Справедлив обобщенный закон ассоциативности для умножения, т. е. результат произведения для n сомножителей не зависит от расстановки скобок; единичный элемент 1 - единственный нейтральный элемент (см. теорему 1.3.2).
Проводя индукцию по n, убеждаемся в том, что (a₁+...+a_n)b = a₁b+...+a_nb; b(a₁+...+a_n) = ba₁+...+ba_n.
Так как a0=a(0+0)=a0+a0, то a0=0. Аналогично, 0a=0.
Так как ab+(-a)b=(a+(-a))b=0b=0, то (-a)b=-ab. Аналогично, a(-b)=-ab. Поэтому (-a)(-b)=-(a(-b))=-(-ab)=ab.
(a-b)c=(a+(-b))c=ac+(-b)c=ac-bc, c(a-b)=c(a+(-b))=ca+c(-b)=ca-cb, т. е. дистрибутивность для разности.

Лемма 1.10.3 (бином Ньютона). Пусть R - кольцо с 1, 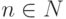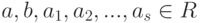$n\in N$ , $a,b,a_1,a_2,...,a_s\in R$ . Тогда:

если ab=ba, то $(a+b)^n=\sum_{k=0}^{n}C_n^k a^k b^{n-k},\ \ \text{где}\ \ C_n^k=\frac{n!}{k!(n-k)!},\ \ C_n^0=1;$
если a_ia_j=a_ja_i для всех i, j, то 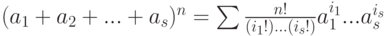$(a_1+a_2+...+a_s)^n = \sum \frac{n!}{(i_1!)... (i_s!)}a_1^{i_1}... a_s^{i_s}$ , где суммирование происходит по всем s -строчкам (i₁,i₂,...,i_s) таким, что i₁+i₂+...+i_s=n.

Доказательство.

Индукция по n с учетом равенства 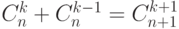$C_n^k+C_n^{k-1}=C_{n+1}^{k+1}$ для k<n и применением перестановочности элементов a и b и закона дистрибутивности.
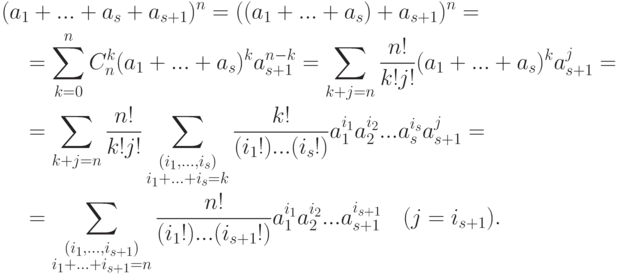
Индукция по s ; s=2 - пункт 1); если утверждение верно для s, то по 1): $\begin{align*} & (a_1+...+a_s+a_{s+1})^n=((a_1+...+a_s)+a_{s+1})^n={} \\ & \quad {}=\sum_{k=0}^{n} C_n^k (a_1+...+a_s)^k a_{s+1}^{n-k}= \sum_{k+j=n} \frac{n!}{k!j!}(a_1+...+a_s)^k a_{s+1}^j={} \\ & \quad {}=\sum_{k+j=n} \frac{n!}{k!j!} \sum_{\substack{(i_1,...,i_s)\\ i_1+...+i_s=k}} \frac{k!}{(i_1!)... (i_s!)}a_1^{i_1}a_2^{i_2}... a_s^{i_s}a_{s+1}^j={} \\ & \quad {}=\sum_{\substack{(i_1,...,i_{s+1})\\ i_1+...+i_{s+1}=n}} \frac{n!}{(i_1!)... (i_{s+1}!)} a_1^{i_1}a_2^{i_2}... a_{s+1}^{i_{s+1}}\quad (j=i_{s+1}). \end{align*}$

Определение 1.10.4. Подмножество S кольца R называется подкольцом, если:

а) S - подгруппа относительно сложения в группе (R,+) ;

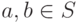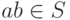б)для $a,b\in S$ имеем $ab\in S$ ;

в)для кольца R с 1 предполагается, что $1\in S$ .

Примеры 1.10.5 (примеры подколец). ${\mathbb Z} \subset {\mathbb Q} \subset {\mathbb R}$

Задача 1.10.6. Описать все подкольца в кольце вычетов Z_n по модулю n.

Замечание 1.10.7. В кольце Z₁₀ элементы, кратные 5, образуют кольцо с 1, не являющееся подкольцом в Z₁₀ (у этих колец различные единичные элементы).

Определение 1.10.8. Если R - кольцо, $a,b\in R$ и $a\ne 0$ , $b\ne 0$ , ab=0, то элемент a называется левым делителем нуля в R, элемент b называется правым делителем нуля в R.

Замечание 1.10.9. В коммутативных кольцах, естественно, нет различий между левыми и правыми делителями нуля.

Пример 1.10.10. В Z, Q, R нет делителей нуля.

Пример 1.10.11. Кольцо непрерывных функций C[0,1] имеет делители нуля. Действительно, если

то 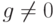$f\ne 0$ , $g\ne 0$ , fg=0.

Пример 1.10.12. Если n=kl, 1<k,l<n, то 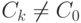$C_k\ne C_0$ , $C_l\ne C_0$ , но C_kC_l=C₀, т. е. кольцо вычетов Z_n по составному числу n имеет делители нуля.

Лемма 1.10.13. Если в кольце R нет (левых) делителей нуля, то из ab=ac, где 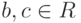$0\ne a\in R$ , $b,c\in R$ , следует, что b=c (т. е. возможность сокращать на ненулевой элемент слева, если нет левых делителей нуля; и справа, если нет правых делителей нуля).

Доказательство. Если ab=ac, то a(b-c)=0. Так как a не является левым делителем нуля, то b-c=0, т. е. b=c.

Определение 1.10.14. Элемент $x\in R$ называется нильпотентным, если xⁿ=0 для некоторого $0<n\in N$ . Наименьшее такое натуральное число n называется степенью нильпотентности элемента .

Ясно, что нильпотентный элемент является делителем нуля (если n>1, то 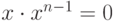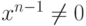$x\cdot x^{n-1}=0$ , $x^{n-1}\ne 0$ ). Обратное утверждение неверно (в Z₆ нет нильпотентных элементов, однако 2, 3, 4 - ненулевые делители нуля).

Упражнение 1.10.15. Кольцо Z_n содержит нильпотентные элементы тогда и только тогда, когда n делится на m², где 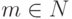$m\in N$ , $m\ne 1$ .

Определение 1.10.16. Элемент x кольца R называется идемпотентом, если x²=x . Ясно, что 0²=0, 1²=1. Если x²=x и 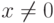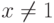$x\ne 0$ , $x\ne 1$ , то x(x-1)=x²-x=0, и поэтому нетривиальные идемпотенты являются делителями нуля.

Через U(R) обозначим множество обратимых элементов ассоциативного кольца R, т. е. тех 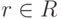$r\in R$ , для которых существует обратный элемент s=r^-1 (т. е. rr^-1=1=r^-1r ).

Лемма 1.10.17. U(R) является группой относительно операции умножения.

Доказательство.

1) Если $r,s\in U(R)$ , то $rs\in U(R)$ , поскольку (rs)^-1=s^-1r^-1.
2) $1\in U(R)$ .
3) Если $r\in U(R)$ , то (r^-1)^-1=r, т. е. $r^{-1}\in U(R)$ .

Пример 1.10.18. U(Z)={1,-1}, $U(Q)=Q^*=Q\setminus\{0\}$ , U(R)=R^*.

Пример 1.10.19. $U(C[0,1])=\{f\in C[0,1]\mid f(x)\ne 0\ \forall x\in [0,1]\}$ .

Пример 1.10.20. Пусть Z_m={C₀,C₁,...,C_m-1}, C_k=k+mZ, - кольцо вычетов по модулю m. Отметим, что 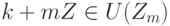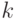$k+mZ\in U(Z_m)$ , $k\inZ$ , тогда и только тогда, когда (k+mZ)(l+mZ)=1+mZ для некоторого 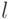$l\inZ$ , т. е. kl+mZ=1+mZ, что означает kl=1+mq, 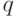$q\inZ$ , т. е. (k,m)=1.

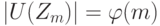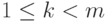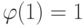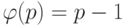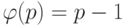Итак, $|U(Z_m)|=\varphi(m)$ , где $\varphi(m)$ - число натуральных чисел $1 \leq k<m$ , не имеющих нетривиальных общих делителей с числом m (функция Эйлера). В частности, $\varphi(1)=1$ , $\varphi(2)=1$ , $\varphi(3)=2$ , $\varphi(4)=2$ , $\varphi(p)=p-1$ для простого числа p. Более того, если $p\in N$ , то $\varphi(p)=p-1$ тогда и только тогда, когда p - простое число.

Задача 1.10.21. Докажите, что группа U(Z_n) циклическая тогда и только тогда, когда 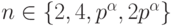$n\in \{2,4,p^{\alpha}, 2p^{\alpha}\}$ , где p - нечетное простое число.

Дальше >>

Авторизоваться

Введение в алгебру

Кольца. Поля. Идеалы и гомоморфизмы колец

Кольца

Свойства колец (R,+,.)

Вопросы и ответы