Основные алгебраические структуры и операции
Обобщенная ассоциативность (применение ассоциативной операции к n сомножителям при n >= 3
Рассмотрим ассоциативную операцию * на множестве M,  ,
, 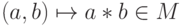 для
для 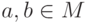 , при этом
, при этом
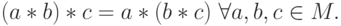
Для одного или двух сомножителей нет вопроса о различных расстановках скобок: a, a*b. Для трех сомножителей a, b, c существует всего две расстановки скобок (a*b)*c, a*(b*c), обозначающие применение бинарной операции * (каждый раз применяемой к двум элементам). На множестве из четырех элементов a1, a2, a3, a4 расстановок скобок уже значительно больше: ((a1*a2)*a3)*a4 (регулярная слева расстановка), (a1*a2)*(a3*a4), (a1*(a2*a3))*a4, a1*((a2*a3)*a4), a1*(a2*(a3*a4)) (регулярная справа расстановка).
Задача 1.3.1 (трудная).
Найти число всех различных расстановок скобок для применения бинарной операции на n сомножителях.
Определение ассоциативной бинарной операции ( (a*b)*c=a*(b*c) для всех  ) означает, что для трех сомножителей результат применения операции не зависит от расстановки скобок (т. е. порядка ее применения). Наша ближайшая цель - показать, что для ассоциативной бинарной операции это утверждение верно и для n сомножителей a1,a2,...,an (при всех расстановках скобок после соответствующего применения операции * мы получаем один и тот же элемент, который можно обозначить a1*a2*...*an, без указания расстановки скобок).
) означает, что для трех сомножителей результат применения операции не зависит от расстановки скобок (т. е. порядка ее применения). Наша ближайшая цель - показать, что для ассоциативной бинарной операции это утверждение верно и для n сомножителей a1,a2,...,an (при всех расстановках скобок после соответствующего применения операции * мы получаем один и тот же элемент, который можно обозначить a1*a2*...*an, без указания расстановки скобок).
Теорема 1.3.2.
Пусть * - бинарная ассоциативная операция на множестве M 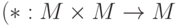 ,
, 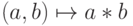 для
для 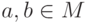 , и
, и  для всех
для всех 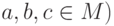 ,
, 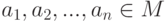 ,
,  . Тогда результат применения операции * к n сомножителям a1,a2,...,an не зависит от расстановки скобок.
. Тогда результат применения операции * к n сомножителям a1,a2,...,an не зависит от расстановки скобок.
Доказательство проведем индукцией по n по вполне упорядоченному множеству 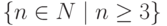 , это означает, что любое непустое подмножество этого множества имеет наименьший элемент.
, это означает, что любое непустое подмножество этого множества имеет наименьший элемент.
Начало индукции n=3 обеспечено определением ассоциативной операции.
Допустим, что утверждение верно для всех k, 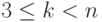 . Рассмотрим произвольную расстановку скобок на n сомножителях a1,a2,...,an, соответствующую применениям бинарной операции * (каждый раз к двум элементам). Наша цель - доказать, что результат применения операции * для произвольной расстановки скобок совпадает с результатом применения для регулярной слева расстановки скобок (... ((a1*a2)*a3)*...)*an. При этом для n=2 имеем a1*a2, а для n=1 имеем a1.
. Рассмотрим произвольную расстановку скобок на n сомножителях a1,a2,...,an, соответствующую применениям бинарной операции * (каждый раз к двум элементам). Наша цель - доказать, что результат применения операции * для произвольной расстановки скобок совпадает с результатом применения для регулярной слева расстановки скобок (... ((a1*a2)*a3)*...)*an. При этом для n=2 имеем a1*a2, а для n=1 имеем a1.
В каждой расстановке скобок есть последнее применение операции * (например: 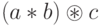 ;
;  ;
; 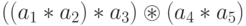 , здесь
, здесь  обозначает последнее применение операции * в каждой из приведенных расстановок). Таким образом, последнее применение операции * происходит к произведению k сомножителей a1,a2,...,ak с некоторой расстановкой скобок и к произведению (n-k) сомножителей ak+1,...,an с некоторой расстановкой скобок, при этом
обозначает последнее применение операции * в каждой из приведенных расстановок). Таким образом, последнее применение операции * происходит к произведению k сомножителей a1,a2,...,ak с некоторой расстановкой скобок и к произведению (n-k) сомножителей ak+1,...,an с некоторой расстановкой скобок, при этом 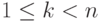 ,
,  . Результат произведения операции * в левом и правом блоке не зависит от расстановки скобок (возможно, k=1 или k=2 ; возможно, n-k=1 или n-k=2 ; если
. Результат произведения операции * в левом и правом блоке не зависит от расстановки скобок (возможно, k=1 или k=2 ; возможно, n-k=1 или n-k=2 ; если 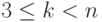 , то в силу индуктивного предположения; если
, то в силу индуктивного предположения; если  , то также в силу индуктивного предположения). Выберем в левом произведении регулярную слева расстановку скобок, а в правом произведении - регулярную справа расстановку скобок. Тогда имеем, применяя последовательно ассоциативность для трех сомножителей, [(... ((a1*a2)*a3)... ak-1)*ak]*[ak+1*(ak+2*(... (an-1*an)... ))]=[((... ((a1*a2)*a3)... ak-1)*ak)*ak+1]*[ak+2*(... (an-1*an)... )]=...= ((a1*a2)*a3)... an-1)*an
(в наших обозначениях, если k=1, то [a1]=a1 ; аналогично, если n-k=1, то [an]=an ).
, то также в силу индуктивного предположения). Выберем в левом произведении регулярную слева расстановку скобок, а в правом произведении - регулярную справа расстановку скобок. Тогда имеем, применяя последовательно ассоциативность для трех сомножителей, [(... ((a1*a2)*a3)... ak-1)*ak]*[ak+1*(ak+2*(... (an-1*an)... ))]=[((... ((a1*a2)*a3)... ak-1)*ak)*ak+1]*[ak+2*(... (an-1*an)... )]=...= ((a1*a2)*a3)... an-1)*an
(в наших обозначениях, если k=1, то [a1]=a1 ; аналогично, если n-k=1, то [an]=an ).
Итак, результат применения операции * в соответствии с исходной (произвольной) расстановкой скобок совпал с результатом применения при регулярной слева расстановке скобок. Таким образом, результат применения ассоциативной операции не зависит от расстановки скобок.
