| Гамбия |
Краткий обзор алгоритмов интеллектуального анализа данных. Алгоритмы взаимосвязей и кластеризации последовательностей
Алгоритм взаимосвязей
Алгоритм взаимосвязей или ассоциативных правил (AssociationRules) позволяет выявить часто встречающиеся сочетания элементов данных и использовать обнаруженные закономерности для построения прогноза. Классический пример - это анализ покупательской корзины, когда проводится поиск товаров, наиболее часто встречающихся в одном заказе (чеке, транзакции), после чего, на основе выявленных закономерностей становится возможной выдача рекомендаций. С помощью надстроек интеллектуального анализа данных для Excel подобная задача решается в "Использование инструментов "Prediction Calculator" и "ShoppingbasketAnalysis"" .
Пример набора правил, формируемых подобным, алгоритмом приведен на рис. 11.1. Предметная область - торговля велосипедами и связанными спортивными товарами. Для примера, первое правило говорит о том, что если в заказе присутствует держатель для велосипедной фляги и кепка, с высокой вероятностью будет приобретена и сама фляга.
Когда подобный набор правил сформирован, его можно использовать, например, для формирования рекомендаций. Скажем, покупателю держателя фляги и кепки, предложат обратить внимание и на имеющиеся фляги. Вопрос заключается в том, как сформировать подобные правила.
Для выявления часто встречающихся наборов объектов может использоваться алгоритм Apriori, реализация которого лежит в основе и MicrosoftAssociationRules, использующегося в SQLServer 2008 [1,2]. Алгоритм Apriori последовательно выделяет часто встречающиеся одно-, двух- и т.д., n-элементные наборы.На i-м этапе выделяются i-элементные наборы. Причем сначала выполняется формирование наборов-кандидатов, после чего для них рассчитывается поддержка.
Поддержка (англ. support) используется для измерения популярности набора элементов. Например, поддержка набора элементов {A,B} - общее количество транзакций, которые содержат как A, так и B.Чтобы сократить запись, здесь и далее указывается просто A и B, а не A=Existing, B=Existing, как на рис. 11.1 (existingс англ. "присутствует").
Чтобы количественно охарактеризовать правило, используется вероятность (англ. probability). Этот же показатель иногда называется достоверностью.
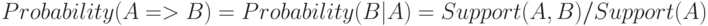
Вероятность для набора 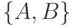 рассчитывается как отношение числа транзакций, содержащих этот набор, к общему числу транзакций.
рассчитывается как отношение числа транзакций, содержащих этот набор, к общему числу транзакций.
Чтобы оценить взаимную зависимость элементов используется важность (англ. importance) или показатель интереса.
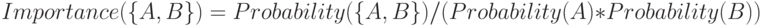
Если 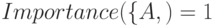 , то A и B - независимые элементы.
, то A и B - независимые элементы.  означает, что A и B имеют положительную корреляцию (клиент купивший товар A вероятно купит и B).
означает, что A и B имеют положительную корреляцию (клиент купивший товар A вероятно купит и B).  указывает на отрицательную корреляцию.
указывает на отрицательную корреляцию.
Для правил важность рассчитывается как логарифм отношения вероятностей:
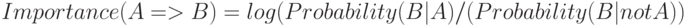
В данном случае равная 0 важность означается, что между A и B нет взаимосвязи. Положительная важность означает, что вероятность B повышается, когда справедливо A; отрицательная - вероятность B понижается, когда справедливо A.
Настройками пороговых значений можно регулировать максимальное число элементов в рассматриваемых наборах, минимальную вероятность при которой правило будет рассматриваться, минимальную поддержку для рассматриваемых наборов и т.д.
Кластеризация последовательностей
Как было рассмотрено выше, алгоритмами ассоциативных правил (взаимосвязей) выявляются часто встречающиеся наборы элементов. Задача кластеризации последовательностей в чем-то схожая - выявить часто встречающиеся последовательности событий. Важное различие заключается в том, что в данном случае учитывается, в какой очередности события происходят (или элементы добавляются в набор). Схожие последовательности объединяются в кластеры. Кроме анализа характеристик кластеров, возможно решение задачи прогнозирования наступления событий на основании уже произошедших ранее.
Примеры применения подобных алгоритмов - анализ переходов по страницам web-сайтов, анализ событий, предшествовавших сбоям в работе информационной системы, и т.д.
Используемый аналитическими службами SQLServer 2008 алгоритм Micorosoft Sequence Clustering - это гибридный алгоритм, сочетающий методы кластеризации с анализом марковских цепей. Анализируемое множество вариантов формируется с использованием вложенных таблиц. В таблице 11.1 представлен условный пример подобного варианта интеллектуального анализа. Важно, чтобы вложенная таблица содержала собственный идентификатор, который позволил бы определить последовательность элементов.
| Идент. Пользователя | Расположение | Идент. послед. | Тематика |
|---|---|---|---|
| 1 | Санкт-Петербург | 1 | Главная страница |
| 2 | Велосипеды | ||
| 3 | Запчасти | ||
| 4 | Велосипеды |
С помощью марковских моделей анализируется направленный граф, хранящий переходы между различными состояниями. Алгоритм MicrosoftSequenceClustering использует марковские цепи n-го порядка.Число n говорит о том, сколько состояний использовалось для определения вероятности текущих состояний. В модели первого порядка вероятность текущего состояния зависит только от предыдущего состояния. В марковской цепи второго порядка вероятность текущего состояния зависит от двух предыдущих состояний, и так далее. Вероятности перехода между состояниями хранятся в матрице переходов. По мере удлинения марковской цепи размер матрицы растет экспоненциально, соответственно растет и время обработки, что надо учитывать при решении практических задач.
Далее алгоритм изучает различия между всеми возможными последовательностями, чтобы определить, какие последовательности лучше всего использовать в качестве входных данных для кластеризации. Созданный алгоритмом список вероятных последовательностей используется в качестве входных данных для применяемого по умолчанию EM-метода кластеризации (англ. Expectation Maximization, максимизации ожидания). Целями кластеризации являются как связанные, так и не связанные с последовательностями атрибуты. У каждого кластера есть марковская цепь, представляющая полный набор путей, и матрица, содержащая переходы и вероятности последовательности состояний. На основе начального распределения используется правило Байеса для вычисления вероятности любого атрибута, в том числе последовательности, в конкретном кластере.