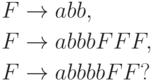|
Упражнение 2.1.25 |
Основные свойства автоматных языков
3.4. Примеры неавтоматных языков
Пример 3.4.1.
Рассмотрим язык 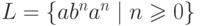 над алфавитом
над алфавитом  .
Утверждение леммы 3.3.1
не выполняется ни для какого натурального числа p.
Действительно, если w = abpap,
то x = abk, y = bm, z = bp-k-map
для некоторых
.
Утверждение леммы 3.3.1
не выполняется ни для какого натурального числа p.
Действительно, если w = abpap,
то x = abk, y = bm, z = bp-k-map
для некоторых  и
и  или
или 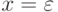 , y = abl, z = bp-lap
для некоторого
, y = abl, z = bp-lap
для некоторого  .
В обоих случаях
.
В обоих случаях  .
Таким образом,
язык L
не является автоматным.
.
Таким образом,
язык L
не является автоматным.
Упражнение 3.4.2.
Пусть 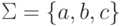 .
При каких словах
.
При каких словах  и
и  язык
язык  является автоматным?
является автоматным?
Замечание 3.4.3. Условие, сформулированное в лемме 3.3.1, является необходимым для автоматности, но не достаточным.
Пример 3.4.4.
Пусть  .
Рассмотрим язык L = {akbman | k=0 или m=n}.
Положим p = 1.
Тогда для любого слова
.
Рассмотрим язык L = {akbman | k=0 или m=n}.
Положим p = 1.
Тогда для любого слова 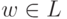 длины не меньше p
найдутся слова
длины не меньше p
найдутся слова 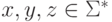 ,
соответствующие утверждению леммы 3.3.1.
Тем не менее язык L
не является автоматным, так как
,
соответствующие утверждению леммы 3.3.1.
Тем не менее язык L
не является автоматным, так как

Лемма 3.4.5*. Пусть L - автоматный язык над алфавитом  . Тогда найдется такое положительное целое число p, что для любого слова
. Тогда найдется такое положительное целое число p, что для любого слова 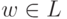 можно подобрать слова
можно подобрать слова 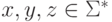 , для которых верно xyz = w,
, для которых верно xyz = w, ![| y | \geqslant [ | w | / p ]](/sites/default/files/tex_cache/3157a353c1a1c3131000c0547474c9fa.png) и
и 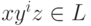 для всех
для всех  .
Здесь [m]
означает целую часть числа m.
.
Здесь [m]
означает целую часть числа m.
Доказательство.
Пусть L
распознается конечным автоматом  ,
содержащим только переходы с метками длины единица.
Положим p = |Q|.
Пусть слово w
является меткой успешного пути
,
содержащим только переходы с метками длины единица.
Положим p = |Q|.
Пусть слово w
является меткой успешного пути 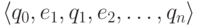 .
Обозначим l = [|w|/p].
Если l = 0,
то положим
.
Обозначим l = [|w|/p].
Если l = 0,
то положим 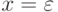 и
и  .
Пусть
.
Пусть  .
Согласно принципу Дирихле найдутся такие натуральные числа j и k,
что
.
Согласно принципу Дирихле найдутся такие натуральные числа j и k,
что  и qjl = qkl.
Выберем слова x, y и z
так, что |x| = jl, |y| = kl - jl
и xyz = w.
и qjl = qkl.
Выберем слова x, y и z
так, что |x| = jl, |y| = kl - jl
и xyz = w.
Упражнение 3.4.6. Является ли автоматным язык

Упражнение 3.4.7. Является ли автоматным язык

Упражнение 3.4.8. Является ли автоматным язык
 множества
множества  и
и  равномощны?
равномощны?
Упражнение 3.4.9. Является ли автоматным язык
 множества
множества  и
и  равномощны?
равномощны?
Упражнение 3.4.10. Является ли автоматным язык

Упражнение 3.4.11. Является ли автоматным язык, порождаемый грамматикой