|
Упражнение 2.1.25 |
Детерминированные контекстно-свободные языки
12.2*. Свойства класса детерминированных языков
Теорема 12.2.1. Каждый автоматный язык является детерминированным контекстно-свободным языком.
Доказательство. Утверждение следует из теоремы 2.7.1.
Лемма 12.2.2. Каждый детерминированный МП-автомат  эквивалентен некоторому детерминированному МП-автомату
эквивалентен некоторому детерминированному МП-автомату  , где для каждого перехода
, где для каждого перехода  выполняется неравенство
выполняется неравенство  .
.
Доказательство.
Пусть дан детерминированный МП-автомат 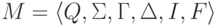 .
Назовем избытком
перехода
.
Назовем избытком
перехода

 .
Докажем лемму индукцией по сумме избытков всех переходов.
.
Докажем лемму индукцией по сумме избытков всех переходов.Шаг индукции. Пусть существует переход

Случай 1.  .
Обозначим первый символ слова x0 через a0.
Преобразуем МП-автомат M в эквивалентный ему
детерминированный МП-автомат
с меньшей суммой избытков всех переходов.
Для этого добавим новое состояние r и переход
.
Обозначим первый символ слова x0 через a0.
Преобразуем МП-автомат M в эквивалентный ему
детерминированный МП-автомат
с меньшей суммой избытков всех переходов.
Для этого добавим новое состояние r и переход  .
Каждый переход вида
.
Каждый переход вида  заменим на переход
заменим на переход  .
К полученному таким образом
детерминированному МП-автомату
применимо предположение индукции.
.
К полученному таким образом
детерминированному МП-автомату
применимо предположение индукции.
Случай 2.  .
Обозначим первый символ слова
.
Обозначим первый символ слова  через C0.
Преобразуем МП-автомат M
в эквивалентный ему
детерминированный МП-автомат
с меньшей суммой избытков всех переходов.
Для этого добавим новое состояние r
и переход
через C0.
Преобразуем МП-автомат M
в эквивалентный ему
детерминированный МП-автомат
с меньшей суммой избытков всех переходов.
Для этого добавим новое состояние r
и переход  .
Каждый переход вида
.
Каждый переход вида  заменим на переход
заменим на переход  .
К полученному таким образом
детерминированному МП-автомату
применимо предположение индукции.
.
К полученному таким образом
детерминированному МП-автомату
применимо предположение индукции.
Случай 3.
Существует переход  .
Тогда переходы
.
Тогда переходы  и
и  совместны.
Противоречие.
совместны.
Противоречие.
Случай 4.
Существуют переход  и переход
и переход  ,
где
,
где  и
и  .
Тогда переходы
.
Тогда переходы  и
и  совместны.
Противоречие.
совместны.
Противоречие.
Лемма 12.2.3. Каждый детерминированный МП-автомат  эквивалентен некоторому детерминированному МП-автомату
эквивалентен некоторому детерминированному МП-автомату  , где каждый переход
, где каждый переход  удовлетворяет условиям
удовлетворяет условиям  и
и  .
.
Доказательство.
Сначала применим лемму 12.2.2,
затем преобразуем МП-автомат так, чтобы
для каждого перехода  выполнялось неравенство
выполнялось неравенство  (см. пример 10.2.4),
и в заключение заменим каждый переход вида
(см. пример 10.2.4),
и в заключение заменим каждый переход вида  на два последовательных перехода
(см. пример 10.2.5).
на два последовательных перехода
(см. пример 10.2.5).
Лемма 12.2.4. Пусть  ,
, 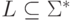 и язык
и язык  порождается некоторым детерминированным МП-автоматом.
Тогда этот язык порождается также
некоторым детерминированным МП-автоматом
порождается некоторым детерминированным МП-автоматом.
Тогда этот язык порождается также
некоторым детерминированным МП-автоматом  , где
, где  ,
,  ,
,

 ,
,  и каждый переход
и каждый переход
 и
и  .
.Доказательство.
Применив лемму 12.2.3,
получим детерминированный МП-автомат  .
Построим искомый МП-автомат
.
Построим искомый МП-автомат  ,
положив
,
положив  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,

Теорема 12.2.5. Язык 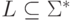 является детерминированным контекстно-свободным языком
тогда и только тогда, когда найдется такой детерминированный МП-автомат
является детерминированным контекстно-свободным языком
тогда и только тогда, когда найдется такой детерминированный МП-автомат  , что
, что

Доказательство. Достаточность проверяется легко. Докажем необходимость. Рассмотрим МП-автомат

Для любых  и
и  введем обозначение
введем обозначение

 для любых
для любых  ,
,  и
и  .
.Построим искомый МП-автомат  ,
положив
,
положив

 обозначается
множество всех подмножеств множества Q2.)
обозначается
множество всех подмножеств множества Q2.)Индукцией по количеству тактов работы можно доказать, что



 .
.Теорема 12.2.6. Пусть L - детерминированный контекстно-свободный язык. Тогда язык L не является существенно неоднозначным.
Доказательство. Пусть дан детерминированный контекстно-свободный язык L. Рассмотрим МП-автомат

 .
Стирая в этой грамматике все вхождения символа
.
Стирая в этой грамматике все вхождения символа  ,
получим контекстно-свободную грамматику G',
порождающую язык L.
,
получим контекстно-свободную грамматику G',
порождающую язык L.Так как
МП-автомат M
не содержит переходов,
ведущих из Q2
в Q1,
а символ  встречается только на переходах,
ведущих из Q1
в Q2,
то в каждом G' -выводе однозначно определяется правило,
которому в G
соответствует правило, содержащее
встречается только на переходах,
ведущих из Q1
в Q2,
то в каждом G' -выводе однозначно определяется правило,
которому в G
соответствует правило, содержащее  .
Поэтому существует естественное однозначное соответствие между
деревьями вывода в грамматике G'
и деревьями вывода в грамматике G
(при этом кроны соответствующих друг другу деревьев различаются только
символом
.
Поэтому существует естественное однозначное соответствие между
деревьями вывода в грамматике G'
и деревьями вывода в грамматике G
(при этом кроны соответствующих друг другу деревьев различаются только
символом  ).
Следовательно, грамматика G' тоже является однозначной.
).
Следовательно, грамматика G' тоже является однозначной.
Теорема 12.2.7. Дополнение каждого детерминированного контекстно-свободного языка является детерминированным контекстно-свободным языком.
Доказательство можно найти в [7, c. 110-116] или [2, c. 212-217].
Пример 12.2.8.
Язык  над алфавитом {a,b,c}
не является детерминированным контекстно-свободным языком,
так как его дополнение не является контекстно-свободным.
над алфавитом {a,b,c}
не является детерминированным контекстно-свободным языком,
так как его дополнение не является контекстно-свободным.
Теорема 12.2.9. Неверно, что для любых детерминированных контекстно-свободных языков L1 и L2 язык 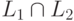 тоже является детерминированным контекстно-свободным языком.
тоже является детерминированным контекстно-свободным языком.
Доказательство. Достаточно рассмотреть детерминированные контекстно-свободные языки L1 и L2 из доказательства теоремы 9.5.1.
Теорема 12.2.10. Неверно, что для любых детерминированных контекстно-свободных языков L1 и L2 язык 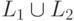 тоже является детерминированным контекстно-свободным языком.
тоже является детерминированным контекстно-свободным языком.
Доказательство. Утверждение следует из теорем 12.2.7 и 12.2.9 и закона де Моргана.
Упражнение 12.2.11. Является ли детерминированным
контекстно-свободный язык  ?
?

