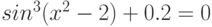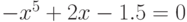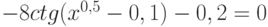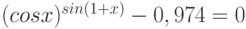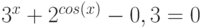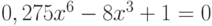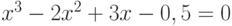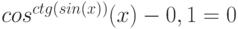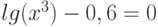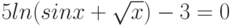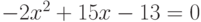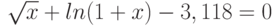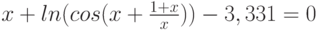|
Есть такие задания, и они никак не принимаются. Притом ошибки только по этим заданиям, в какой бы последовательности я их не заполнял. Как их заполнять??? Инструкций в заданиях нет. Там через запятые, подряд как число, через пробел, или надо текст весь писать через запятую или точку? Задание: Пронумеруйте шаги Создание имени путем выделения ячеек на листе: |
Анализ данных посредством инструмента "Подбор параметра"
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
При решении экономических и финансовых задач достаточно часто решение задачи приобретает вид математической модели (формулы), построенной на основе выявленных связей между изучаемыми элементами явления (результативного показателя) и самим явлением в целом. Изменяя составляющие элементы, можно проводить анализ изменения явления в целом. Таким образом, изучаются свойства и значения функции (явления) в тех или иных условиях. Этот анализ позволяет проводить инструмент MS Excel Подбор параметра. Рассмотрим возможности его применения на конкретных примерах.
Нахождение значения аргумента функции, соответствующего определённому значению функции
Использование функции Подбор параметра для нахождения значения аргумента функции, соответствующего заданному значению функции может быть представлено таким образом: поиск определенного результата для ячейки с помощью подбора значения другой ячейки.
Например, одна ячейка содержит формулу, в которой есть ссылки на другую ячейку.
Значение в ячейке С1 представляет собой среднее арифметическое значение в ячейках А1 и В1:
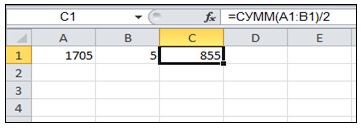
Допустим, что для целей исследования необходимо найти значение, которое должна принять ячейка А1, для того чтобы ячейка С1 приняла значение 855.
Безусловно, можно самостоятельно путём перебора значений в ячейке А1 достичь необходимый результат. Однако, в целях минимизации затрат времени следует воспользоваться функцией Подбор параметра.
Для этого необходимо:
1) выполнить команду Подбор параметра из меню Данные > Анализ "что-если".
В результате появится запрос Подбор параметра:

2) в поле Установить в ячейке ввести ссылку или имя ячейки, содержащую формулу, для которой следует подобрать параметр. Автоматически в поле Установить в ячейке отображается имя ячейки, которая была активной на момент выполнения команды Подбор параметра. Кнопка свёртывания окна диалога, расположенная справа от поля, позволяет временно убрать диалоговое окно с экрана, чтобы было удобнее выделить диапазон на листе. Выделив диапазон, следует нажать кнопку для вывода на экран диалогового окна.
3) в поле Значение ввести число, которое должно возвращать формула с искомым значением параметра. Например, 855.
4) в поле Изменяя значение ячейки указать ссылку на ячейку, содержащую параметр, значение которого требуется подобрать для получения требуемого результата. На эту ячейку прямо или косвенно должна ссылаться формула, содержащаяся в ячейке, адрес которой указан в поле Установить в ячейке. В нашем случае это А1.
В итоге диалоговое окно примет следующий вид:
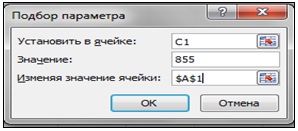
5) нажать кнопку ОК для закрытия диалогового окна. После выполнения этого действия появляется запрос Результат подбора параметра, а искомое значение параметра отображается в ячейке А1:

Использование функции Подбор параметра для нахождения значения аргумента функции при изменении вида ее графика
Допустим, что для решения поставленной задачи нам предстоит проанализировать построенный в Ms Excel график функции y = 3x-5 в диапазоне аргумента от –3 до 6.
Для этого следует:
1) в ячейки А1-А10 ввести значения от –3 до 6 с шагом 1; в ячейку В1 – ввести формулу 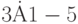 и путём перетаскивания маркера заполнения скопировать эту формулу на ячейки В2-В10. В результате соответствующий участок листа примет следующий вид:
и путём перетаскивания маркера заполнения скопировать эту формулу на ячейки В2-В10. В результате соответствующий участок листа примет следующий вид:
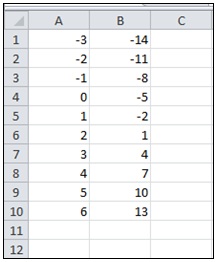
2) выделив диапазон В1-В10, выберите тип диаграммы "График" на вкладке Вставить в группе Диаграммы.
3) На вкладке Макет в группе Подписи нажмите кнопку Подписи данных, а затем выберите нужный параметр отображения.
4) На вкладке Конструктор в группе Данные нажмите Выбрать данные.
5) В появившемся окне Выбор источника данных выберите Подписи горизонтальной оси. Задайте диапазон подписей оси диапазон А1-А10.
В результате должен быть построен график функции:
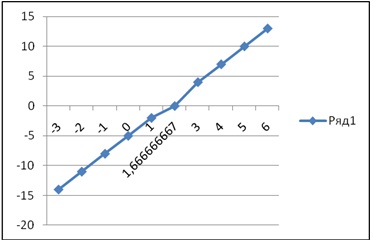
Далее предположим, что необходимо узнать значение аргумента данной функции, при котором значение самой функции будет равно 0.
Чтобы решить эту задачу с помощью построенного графика и функции Подбор параметра необходимо:
1) щелчком левой кнопки мыши на графике выделить ряд данных, содержащий маркер данных, который нужно изменить,
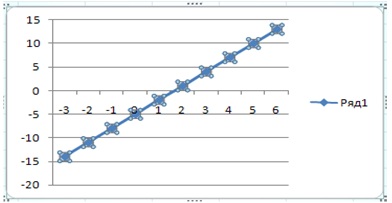
а затем выделить щелчком сам маркер
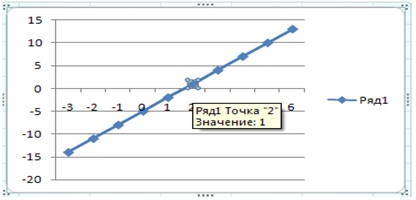
2) в меню Данные > Анализ выбрать функцию Поиск решения
3) если значение маркера данных получено из формулы, появится диалоговое окно Подбор параметра:

4) в поле Оптимизировать целевую функцию отображается ссылка на ячейку, содержащую формулу, в поле Значения – требуемая величина. Так, в данном случае следует указать ячейку В6 и значение "0" соответственно и нажать кнопку ОК.
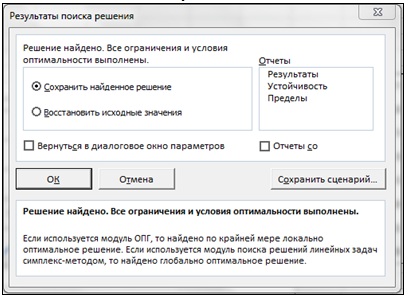
При поиске решения можно изменять только одну ячейку.
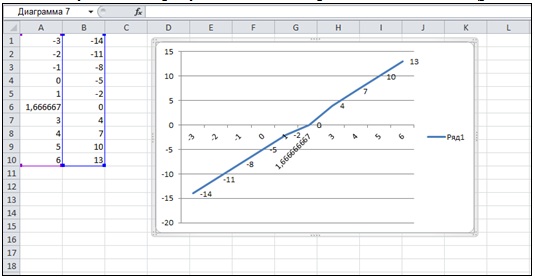
При этом исходное значение аргумента в ряде данных сменится на значение, полученное в результате поиска решения 1,666667 (рис. 11. рис. 11.11).
Решение уравнений
Поиск решения позволяет находить одно значение аргумента, соответствующее заданному значению функции (например, 0). Однако часто функция может принимать одно значение при нескольких значениях аргументов. То есть уравнение может иметь несколько корней. Например, функция 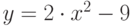 может принимать значение 0 при двух значениях аргументов.
может принимать значение 0 при двух значениях аргументов.
Однако, функция Поиск решения найдет только один корень уравнения – самый близкий к значению в ячейке, указанной в поле Оптимизировать целевую функцию.
Так, если попытаться решить указанное выше уравнение с помощью Ms Excel и встроенной в него функции Подбор параметра, то исходные данные можно представить в следующем виде:
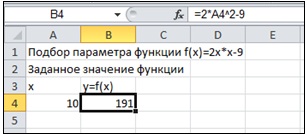
Выполнив команду Подбор параметра из меню Данные > Анализ "Что-если", необходимо заполнить поля диалогового окна следующим образом:
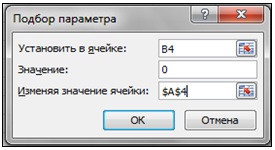
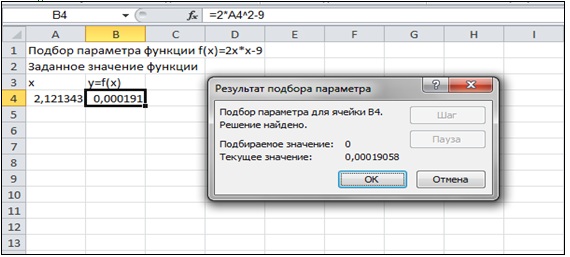
В результате найденным корнем уравнения будет значение 2,121343 в ячейке А4 (рис. 11. рис. 11.14).
Однако, это не единственный корень. В этом можно убедиться, решив уравнение или построив график функции 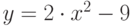 .
.
Для построения графика следует:
- в ячейки С4-С24 ввести значения от –10 до 10 с шагом 1; в ячейку D4 – ввести формулу 2*C4*C4-9 и путём перетаскивания маркера заполнения заполнить этой формулой ячейки D5-D24;
- выделив диапазон D4-D24, выбрать тип диаграммы График в меню Вставка > Диаграммы;
- На вкладке Конструктор в группе Данные нажмите Выбрать данные.
- В появившемся окне Выбор источника данных выберите Подписи горизонтальной оси. Задайте диапазон подписей оси диапазон С4-С24.
В результате должен быть построен график функции:
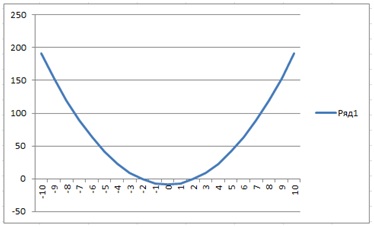
Из графика видно, что уравнение  имеет 2 корня, к тому же эти корни примерно равны –2 и 2. Одни корень 2,121343 нам уже известен.
имеет 2 корня, к тому же эти корни примерно равны –2 и 2. Одни корень 2,121343 нам уже известен.
Для поиска второго корня можно поступить двояко, используя пункт А или Б методических указаний ниже:
А. Изменим значение, например, в ячейке С12 (более близкое к ожидаемому корню). Выделим ячейку D12 и выполним команду Подбор параметра из меню Данные > Анализ "Что-если". Заполним поля запроса:
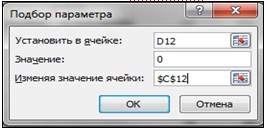
и после щелчка по кнопке ОК в ячейке С12 получим значение второго корня -2,12125:
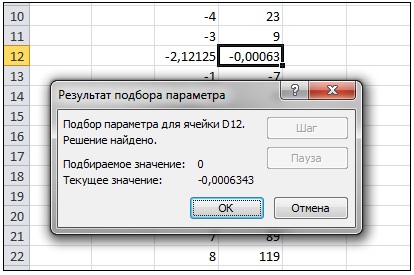
Б. Построим график функции в интервале от -10 до 10.
Щелчком левой кнопки мыши на графике выделим ряд данных, содержащий маркер данных, близкий ко второму корню:
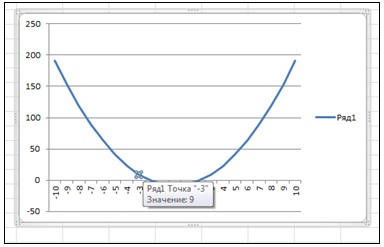
Сделаем активной ячейку D11 со значением функции, равным 9 и в меню Данные > Анализ "что-если" выберем Подбор параметра. Заполним поле Изменяя значение ячейки запроса:
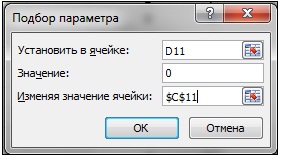
и щелкнув по кнопке ОК, в ячейке С11 получим значение второго корня -2,1213207:

Следует обратить внимание, что значения корня, полученные в п.А и п.Б имеют несущественное отличие. Это вызвано следующим обстоятельством. По умолчанию команда Подбор параметра прекращает итерационные вычисления, когда выполняется 100 итераций, либо при получении результата, который находится в пределах 0,001 от заданного целевого значения. Если нужна большая точность, можно изменить используемые по умолчанию параметры командой Параметры меню Файл > Формулы. Затем на вкладке Параметры вычислений в поле Предельное число итераций введите значение больше 100, а в поле Относительная погрешность – значение меньше 0,001.
Если Ms Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне запроса Результат подбора параметра и прервать вычисления, а затем нажать кнопку Шаг, чтобы просмотреть результаты каждой последовательной итерации. Когда Вы решаете задачу в пошаговом режиме, в этом окне запроса появляется кнопка Продолжить. Нажмите ее, когда решите вернуться в обычный режим подбора параметра.
Задание
Решить уравнение с использованием инструмента ExcelПодбор параметра двумя способами:
- подбором аргумента для конкретного значения функции;
- посредством изменения графика функции.
Удостовериться с помощью построения графика в количестве корней уравнения. Определить все корни.
Варианты.


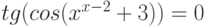
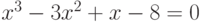
![$\sqrt[3]{x^{4}}-cos(x)+4= 0$](/sites/default/files/tex_cache/3628456d3e8f52959b344fc3b4923721.png)