НОУ ИНТУИТ | Языки логического программирования. Лекция 9: Язык Пролог: чистый недетерминированный Пролог и процедурная семантика

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 06.11.2008 | Уровень: специалист | Доступ: платный | ВУЗ: Ярославский Государственный Университет им. П.Г. Демидова

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать программу

Аннотация: Синтаксис программ и запросов: формальные определения. Подстановки: определение подстановки и результата ее применения к разным выражениям Пролога; частный случай и вариант; унификатор выражений и наиболее общий унификатор и их примеры; интерпретация программы и модель программы; основная модель программы; ответ и правильный ответ; множество всех правильных ответов. Процедурная семантика: отношение выводимости запросов; пространство вычислений и его представление в виде дерева. Адекватность процедурной семантики.

Ключевые слова: программа, атом, левая часть правила, заголовок, правая часть правила, тело правила, факт, предикатный символ, терм, запрос, множество термов программы, множество атомов программы, множество термов без переменных, множество атомов без переменных, семантика, подстановка, частный случай, унификатор выражений, НОУ, унификатор, интерпретация, подмножество, модель программы, множество, модель, множеств фактов без переменных, множество фактов без переменных, модель подстановки, правило без переменных, атом без переменных, заголовок правила, модель множества, основная модель, кортеж термов, правильный ответ, множество всех правильных ответов, арным отношением, шаг вычислений, элементарный шаг вычислений, LIPS, пространство вычислений, непустой запрос, пустой запрос, тупиковое вычисление, успешное вычисление, дерево вычислений, процедурная семантика, кортеж, ответ

Чистый недетерминированный Пролог

Синтаксис программ и запросов

Программа есть множество правил вида:

B₀ <- B₁,...,B_m (m >= 0);

где B₀, B₁,...,B_m – атомы, B₀ – левая часть правила ( заголовок ), B₁,...,B_m – правая часть правила ( тело правила ). Тело правила может быть пустым ( факт ).

Атом имеет следующий вид:

P (t₁,...,t_n);

где P – предикатный символ, $t_{i} (i \in \overline {1,n})$ – термы.

Терм – это либо переменная, либо константа, либо составной терм f(t₁,...,t_k) ; где f – функциональный символ, а 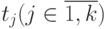$t_{j} (j \in \overline{1,k})$ – термы.

Запрос имеет вид:

<- C₁,...,C_r (r > 0);

где $C_{i} (i \in \overline{1,r})$ – атомы. Каждая программа фиксирует множество употребленных в ней предикатных символов. Только они могут использоваться в запросах к ней.

Введем обозначения:

T – множество термов программы ;

U – множество атомов программы ;

T_h – множество термов без переменных (основных);

U_h – множество атомов без переменных.

Подстановки

Семантика Пролога определяется через подстановки. Подстановка - это функция, действующая из множества X переменных в множество T термов программы:

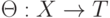
$\Theta : X \to T$

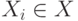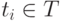(при этом каждой переменной $X_{i} \in X$ ставится в соответствие терм $t_{i} \in T$ ).

$\Theta$ как функция продолжается на множество всех интересующих нас выражений:

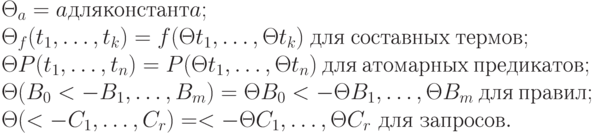
$\Theta _{a} = a для констант a; \\ \Theta _{f}(t_{1},\dots ,t_{k}) = f(\Theta t_{1},\dots ,\Theta t_{k}) \ для \ составных \ термов; \\ \Theta P (t_{1},\dots ,t_{n}) = P (\Theta t_{1},\dots ,\Theta t_{n}) \ для \ атомарных \ предикатов; \\ \Theta (B_{0} <- B_{1},\dots ,B_{m}) = \Theta B_{0} <- \Theta B_{1},\dots ,\Theta B_{m} \ для \ правил; \\ \Theta ( <- C_{1},\dots ,C_{r}) = <- \Theta C_{1},\dots ,\Theta C_{r} \ для \ запросов.$

Результат $\Theta _{e}$ применения подстановки $\Theta$ к выражению e называется частным случаем e. Частный случай есть вариант, если e и $\Theta _{e}$ различаются только именами переменных.

Унификатором выражений A₁ и A₂ называется подстановка $\Theta,$ для которой $\Theta A_{1} = \Theta A_{2}$ .

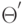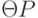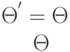Наиболее общим унификатором (НОУ) называется унификатор $\Theta,$ что для любого другого унификатора $\Theta ^{'}$ атом $\Theta ^{'} P$ является частным случаем $\Theta P$ (т. е. $\Theta ^{'} = \Theta ^{"}\Theta$ ).

Пример 1. Атомы P (f (X, a, g(b, Y)), b) и P (f (b,a,Z), X) имеют следующий НОУ:

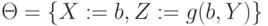
$\Theta = \{ X:=b, Z:=g(b, Y)\}$

и результат подстановки P( f(b, a, g(b, Y)), b). Функция

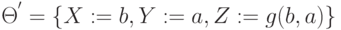
$\Theta ^{'} = \{ X:=b, Y:=a, Z:=g(b, a)\}$

является унификатором, но не НОУ (ее результат P( f(b, a, g(b, a)), b) - частный случай результата подстановки 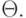$\Theta.$

Пример 2. Атомы P (a, b) и P (b, X) не имеют НОУ (первые термы у них - различные константы).

Перейдем теперь к интерпретациям. Подмножество

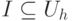
$I \subseteq U_{h}$

(атомов без переменных, т. е. фактов) называется интерпретацией программы.

Интерпретация I называется моделью программы S, если для любого правила 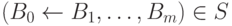$(B_{0} \leftarrow B_{1},\dots , B_{m}) \in S$ и любой подстановки $\Theta,$ где $\Theta B_{0}$ - атом без переменных, имеет место:

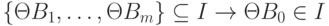$\{ \Theta B_{1},\dots , \Theta B_{m}\} \subseteq I \to \Theta B_{0} \in I$ .

Пусть M(S) - множество всех моделей программы S. Нетрудно видеть, что пересечение двух любых моделей программы S также является моделью этой программы. Действительно, пересечение двух моделей (и потому интерпретаций ) как множеств фактов без переменных также представляет собой множество фактов без переменных, а потому интерпретацию. Так как для исходных моделей подстановка превращает некоторое правило в правило без переменных, то атом без переменных в заголовке правила принадлежит обеим интерпретациям, а следовательно, их пересечению, что и требуется для подтверждения выполнения условия модели.

Наименьшая из всех моделей множества M(S) называется основной моделью I_S.

Рассмотрим запрос <- C₁,..., C_r, и пусть X₁,..., X_k - все переменные запроса и для некоторой подстановки $\Theta$ и интерпретации I имеет место включение

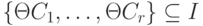
$\{ \Theta C_{1},\dots , \Theta C_{r}\} \subseteq I$

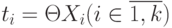(т. е. формула $\Theta C_{1},\dots , \Theta C_{r}$ - истинна в I). Тогда кортеж термов <t₁,..., t_k>, где $t_{i} = \Theta X_{i} (i \in \overline {1,k})$ , называется ответом на запрос интерпретации I.

Ответ называется правильным ответом, если он является ответом основной модели (и для любой другой, конечно).

Множество всех правильных ответов - это k -арное отношение на множестве T_h термов без переменных, т. е. на множестве всех объектов. Если k=0, то при 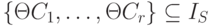$\{ \Theta C_{1},\dots , \Theta C_{r}\} \subseteq I_{S}$ ответ Да, а иначе ответ Нет (0-арное отношение).

Процедурная семантика

Прежде всего опишем шаг вычислений. Пусть запрос Q имеет вид

Q = <- C₁ ..., C_j,..., C_r

и в нем выделен атом C_j и правило

l^' = B₀ <- B₁,..., B_m (m >= 0),

которое является вариантом правила l программы (все переменные отличны от переменных запроса Q ).

Если $\Theta$ - НОУ для C_j и B₀, то будем говорить, что запрос

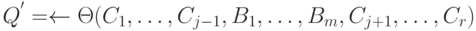
$Q^{'} = \leftarrow \Theta (C_{1},\dots , C_{j-1}, B_{1},\dots , B_{m}, C_{j+1},\dots , C_{r})$

выводим из Q (с помощью правила l и подстановки $\Theta$ ). Получение Q^' из Q - элементарный шаг вычислений в Прологе (он может закончиться и неудачей). Производительность Пролог-машины измеряют количеством таких шагов в секунду (единица LIPS - Logic Interference Per Second).

Пространством вычислений называется множество возможных запросов с заданным отношением выводимости. При вычислении запроса Q мы образуем последовательность запросов:

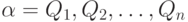
$\alpha = Q_{1}, Q_{2},\dots , Q_{n}$

так, что Q₁=Q и Q_i+1 выводим из Q_i (i=1, 2,...). Если из Q_n не выводим ни один запрос, то вычисления закончены (в некоторых случаях процесс вычислений может идти неограниченно). При окончании вычислений возможны 2 случая:

Q_n - непустой запрос, тогда вычисление тупиковое (неудачное).
Q_n - пустой запрос, тогда $\alpha$ успешное вычисление.

В случае тупикового вычисления мы выбираем следующее подходящее правило, а в случае успешного вычисления мы находим подстановку

$\Theta _{\alpha } = \Theta _{n-1}\Theta _{n-2}\dots \Theta _{2}\Theta _{1}$ ,

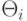где $\Theta _{i}$ - подстановка, с помощью которой запрос Q_i+1 выводим из запроса Q_i.

Пространство вычислений запроса естественно представить деревом, в котором вершины отвечают запросам, а дуги - выводимости. На рис. 9.1 приведено дерево вычислений для примера 2 из предыдущего раздела.

Рис. 9.1.

Адекватность процедурной семантики

Теперь нам надо показать, что в описанной процедурной семантике Пролога мы получаем все необходимое и только это.

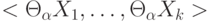Пусть X₁,..., X_k - все переменные запроса Q и $\alpha$ - успешное вычисление Q, а $\Theta _{\alpha }$ - соответствующая подстановка, полученная в процессе этого вычисления. Тогда кортеж $<\Theta _{\alpha } X_{1},\dots , \Theta _{\alpha } X_{k}>$ - ответ, выдаваемый вычислением $\alpha.$ Справедливы следующие утверждения:

Если <t₁,..., t_k> - ответ, то каждый его частный случай, не содержащий переменных, есть правильный ответ.
Каждый правильный ответ <t₁',..., t_k'> на запрос Q является частным случаем некоторого ответа <t₁,..., t_k>, выдаваемого успешным вычислением Q.

Таким образом, пространство вычислений полно с точки зрения логики процедурной семантики.

Упражнения

Постройте для упражнения 3.6.1 дерево вычислений.
Постройте для упражнения 3.6.2 дерево вычислений.
Постройте для упражнения 3.6.3 дерево вычислений.
Постройте для упражнения 3.6.4 дерево вычислений.
Для упражнения 3.9.5 укажите множество интерпретаций прогрммы, множество моделей прогрммы и основную модель.
Для упражнения 3.9.5 укажите один из правильных ответов и ответ, не являющийся правильным.

Дальше >>

Языки логического программирования

Языки логического программирования