Модель Бэкуса алгебры программ: основные конструкции

Общая характеристика модели Бэкуса

В 1978 году выдающийся американский информатик Дж. Бэкус, создатель первых языков программирования ФОРТРАН и АЛГОЛ, в докладе при вручении ему высшей премии по информатике - премии Алана Тьюринга - выдвинул модель алгебры программ. Эта модель является развитием идей языка Рефал в направлении введения форм - структур более мощных, чем функции.

Формы являются функциями высших порядков: если аргументами функции являются данные, то аргументами формы являются функции. Таким образом форма есть алгоритм (программа), который преобразует другой алгоритм (программу). Эта фундаментальная идея позволяет ввести алгебру форм, которая и является алгеброй программ.

Примеры форм известны из математических курсов:

1. Определенный интеграл есть форма, которая функции ставит в соответствие число.
2. Неопределенный интеграл есть форма, которая функции ставит в соответствие другую функцию (вернее даже - некоторое множество других функций).
3. Производная есть форма, которая одной функции ставит в соответствие другую функцию.

Заметим, что в Рефале есть одна форма apply, которая названа функцией порождения процесса (в модели Бэкуса она называется аппликацией). Аргументом этой формы является функциональный терм (другая функция), а значением этой формы - применение функции аргумента к своим данным, т. е. результат выполнения функционального терма.

В модели Бэкуса форма аппликации является фундаментальной наряду с еще 8 формами. Все другие формы строятся из комбинации фундаментальных, а в основу алгебры программ положены как аксиомы алгебраические законы тождества некоторых форм.

Отметим также, что под влиянием этой новой для языков программирования идеи форм в других языках программирования также стали вводиться конструкции форм. Так, например, в языке C++ Б.Страуструп ввел новую конструкцию, названную им алгоритмами, которые фактически являются формами.

Базис модели Бэкуса

В модели Бэкуса определяются 2 скалярных типа:

атом - для данных;

примитивная функция - для программ

и 2 структурных типа:

объект - для данных; конструируется из атомов;

формы - для программ; с их помощью создаются новые функции.

Атомами являются идентификаторы, числа, специальные знаки T и F, а также пустой кортеж, обозначаемый <>.

Объект - это атом или кортеж

<x₁,..., x_n>,

где - либо объект, либо неопределенность, которая изображается как <?>. Примеры объектов: 15, <AB, 1, 2>, <a, < <B, C>, D> >.

Аппликация обозначается как двоеточие ":". Если f - функция, а X - объект, то f:X - результат применения функции к объекту. Примеры:

• + (функция сложения) +:<1, 2> = 3.
• 1 (функция выбора 1-го элемента) 1:<A, B, C> = A.
• 2 (функция выбора 2-го элемента) 2:<A, B, C> = B.
• t1 (функция хвоста кортежа) t1:<A, B, C> = <B, C>.

Функции преобразуют объекты в объекты и сохраняют неопределенность ( f:<?> = <?> ). Результат применения функции к объекту является неопределенностью ( f:X = <?> ) в следующих случаях:

1. результат операции ":" равен <?> ;
2. незавершенная операция ":" (зацикливание).

Примитивные функции

Для описания примитивных функций воспользуемся синтаксисом условного выражения Маккарти:

P₁ -> E₁,..., P_n -> E_n, T -> E.

Здесь - логические условия, а 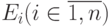- выражения. Семантика вычислений такова: вычисляются последовательно условия до тех пор, пока не найдется истинное значение ( T является тождественно истинным условием) и значение соответствующего выражения (после стрелки с этим условием) становится значением всего выражения. Будем условное выражение Маккарти записывать в виде:

P₁ -> E₁;...; P_n -> E_n; E.

При описании функции будем использовать двойное двоеточие как слово "есть" для отделения описываемой функции и описания при помощи выражения Маккарти:

f:X :: <описание функции>.

Тождественная функция

id:X :: X

Логические функции

Атом

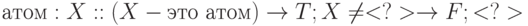
Пусто ( null )

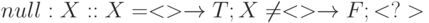
Число ( numb )

Равенство ( eq )

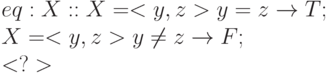
Неравенство ( ne )

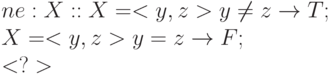
Арифметические операции и отношения

Cумма ( + )

+ : X :: X=<y,z> & numb(y) &  numb(z) -> y+z; <?>

Разность ( - )

- : X :: X=<y,z> & numb(y) &  numb(z) -> y-z; <?>

Произведение ( x )

x : X :: X=<y,z> & numb(y) &  numb(z) -> y*z; <?>

Частное ( )

Больше, чем ( gt )

gt:X  ::  X=<y,z> &  y>z  -> T; 
          X=<y,z> &  y<=z  -> F;
          <?>

Больше или равно ( ge )

ge:X  ::  X=<y,z> &  y>=z  -> T; 
          X=<y,z> &  y<z  -> F;
          <?>

Меньше, чем ( lt )

lt:X  ::  X=<y,z> &  y<z  -> T; 
          X=<y,z> &  y>=z  -> F;
          <?>

Меньше или равно ( le )

le:X  ::  X=<y,z> &  y<=z  -> T; 
          X=<y,z> &  y>z  -> F;
          <?>

Функции кортежей

Селекторы

1:X :: X=<x1,..., xn> -> x1; <?>
s:X :: X=<x1,..., xn> &  n >= s -> xs; <?>

Например,

5  5:<t1, t2,t3, t4, t5, e> = t5,
5  5:<e> = <?>.

Хвост

t1:X :: X=<x1> -> <>; 
        X=<x1,..., xn> &  n >= 2 -> <x2,..., xn>;
        <?>

Расписать левым - кортеж пар из 1-го аргумента и элементов 2-го ( distl )

distl : X :: X=<y,<> > -> ;
             X=<y, <z1,..., zn>>->
                               <<y,z1>,..., <y,zn>>;
             <?>

Расписать правым - кортеж пар из элементов 1-го аргумента и 2-го аргумента ( distr )

distr : X :: X=<<>,y> -> <>;
             X=<<z1,..., zn>, y>->
                                  <<z1, y>,..., <zn, y>>;
             <?>

Присоединить слева - 1-й аргумент ко 2-му ( appendl )

appendl : X :: X=<y, <>> -> <y>;
               X=<y, <z1,..., zn>> -> <y, z1,..., zn>;
               <?>

Присоединить справа - 2-й аргумент к 1-му ( appendr )

appendr : X :: X=<<>, y> -> <y>;
               X=<z1,..., zn>, y> -> <z1,..., zn, y>;
	       <?>

Следующие две функции хотя и задаются как примитивные, могут быть написаны с помощью языка модели Бэкуса (см. далее).

Длина кортежа ( long )

long : X :: X=<> -> 0; X=<x₁,..., x_n> -> n; <?>

Транспонирование матрицы ( trans )

trans : X :: X=<<x11,..., x1m>,
                <x21,..., x2m>, 
                ...
                <xn1,..., xnm>> ->

	     <<x11,..., xn1>,
              <x12,..., xn2>,
              ...
              <x1m,..., xnm>>;
             <?>

Матрица представляется в виде кортежа кортежей.

Конъюнкция ( & )

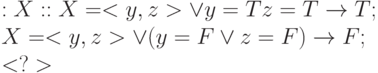
Дизъюнкция ( )

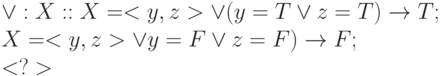
Отрицание ( not )

not : X :: X=T -> F;
           X=F -> T;
           <?>

Упражнения

1. С помощью условного выражения Маккарти и примитивных функций опишите функцию, которая перемножает 2 комплексных числа, заданных кортежами из вещественной и мнимой части.
2. С помощью условного выражения Маккарти и примитивных функций опишите функцию, которая проверяет является ли кортеж матрицы данных квадратной матрицей.
3. С помощью условного выражения Маккарти и примитивных функций опишите функцию, которая сравнивает на равенство 2 комплексных числа заданных кортежами из вещественной и мнимой части.
4. С помощью условного выражения Маккарти и примитивных функций опишите функцию, которая выбирает главную диагональ квадратной матрицы 2-го порядка.