| Россия, Москва |
Умножение чисел с фиксированной запятой в прямом и дополнительном кодах
Умножение с младших разрядов множителя чисел, заданных в дополнительном коде
При умножении чисел, заданных в дополнительном коде, с младших разрядов множителя, так же как и при умножении со старших разрядов множителя в формировании произведения участвует все число, включая его знак. Произведение также получается в дополнительном коде со знаком. Соответствующая формула умножения выглядит следующим образом:
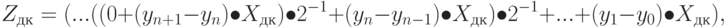 |
( 8.4) |
где y0 – знак множителя;
yn+1 – разряд, дополняющий множитель справа; для дополнительного кода yn+1 ≡ 0 при любом значении знака Yдк.
Так же, как и в предыдущем алгоритме, (yi+1-yi) может принимать три разных значения: (-1), (0), (+1), исходя из чего на каждом шаге вычислений к полученному на предыдущем шаге значению СЧП добавляется Xдк, ноль или (-Xдк) соответственно.
Следует отметить, что, в отличие от аналогичного способа умножения модулей сомножителей в прямом коде, здесь на последнем шаге сдвига вправо нет.
Пример 8.5.
Выполнить умножение с младших разрядов множителя следующих чисел с фиксированной запятой, заданных в дополнительном коде: Xдк = 0.1100; Yдк = 0.0111
Решение.
Пример 8.6.
Перемножим с младших разрядов самые большие (по модулю) числа, которые можно представить в дополнительном коде: Xдк = 0.1111; Yдк = 1.0000.
Решение.
Выполним проверку.
- Знаки сомножителей разные. Результат получился отрицательным.
- |X| = 15/1610; |Y| = 16/1610; |Z| = 0.111100002 = 240/25610.
Это соответствует ожидаемому результату.
Выполним проверку.
- Знаки сомножителей разные. Результат получился отрицательным.
- |X| = 15/1610; |Y| = 16/1610; |Z| = 0.111100002 = 240/25610.
Это соответствует ожидаемому результату.
Краткие итоги
В данной лекции рассмотрены способы умножения чисел с фиксированной запятой, заданных в прямом и дополнительном кодах. Рассмотрено умножение положительных и отрицательных чисел, заданных в прямом и дополнительном кодах, на 2±k как арифметический или логический сдвиг соответствующего числа. Показана связь различных алгоритмов умножения с используемой аппаратурой.
Вопросы и задания
- Назовите способы умножения чисел с фиксированной запятой.
- Какова будет длина произведения, если один сомножитель имеет длину n разрядов, а другой – k разрядов?
- Возможны ли в ЭВМ случаи перемножения операндов разной длины? Если возможны, то накладываются ли на их размеры какие-либо ограничения? Если невозможны, то почему?
- Что такое "укороченная разрядная сетка"? Каковы ее достоинства и недостатки? Где она применяется?
- Почему умножения числа на 2±i равносильно его сдвигу на соответствующее число разрядов влево или вправо?
- Чем отличается логический сдвиг двоичного числа от арифметического?
- Что происходит с разрядами числа, которые при сдвиге вправо выходят за пределы разрядной сетки?
- В каком случае при сдвиге числа влево фиксируется переполнение результата?
- Каким образом определить требования к регистрам, хранящим операнды и служащим для хранения суммы частичных произведений при различных алгоритмах представления операндов и выполнения операции?
- Какие из алгоритмов (для чисел, представленных в прямом или дополнительном кодах, со старших или младших разрядов множителя) требуют бОльших временнЫх затрат и схемотехнических затрат?
- Какой коррекции должна подвергнуться схема выполнения операции умножения в укороченной разрядной сетке по сравнения с получением произведения в 2n-разрядной сетке?
- Выполните перемножение двух чисел 1.1011пк и 0.1011пк, представленных в прямом коде со старших и младших разрядов множителя. Сравните полученные результаты. Объясните возможные несовпадения.
- Выполните перемножение двух чисел 1.1011дк и 0.1011дк, представленных в дополнительном коде со старших и младших разрядов множителя. Сравните полученные результаты. Объясните возможные несовпадения. Сравните полученные результаты с результатами, полученными в задании 12.



