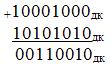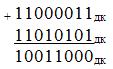Лекция 7: Способы представления чисел в ЭВМ. Сложение чисел в обратном и дополнительном кодах

Модифицированные дополнительный и обратный коды и их использование в операции алгебраического суммирования

В модифицированных кодах кодирование знака осуществляется 2-мя разрядами:

"+" кодируется как "00"

"-" кодируется как "11".

При этом изображение числа X в этих кодах определяется равенствами:

Эта избыточность, сохраняя все качества обычных дополнительного и обратного кодов, дополняет их способностью фиксировать переполнение.

Знаковые разряды результата "01" определяют положительное переполнение в операциях алгебраического суммирования, а "10" – отрицательное.

При этом основная методика выполнения операций алгебраического суммирования в обратном и дополнительном кодах не меняется:

• при алгебраическом суммировании в модифицированном обратном единица, выходящая за пределе знаковых разрядов, должна быть добавлена в младший разряд предварительного результата,
• при алгебраическом суммировании в модифицированном дополнительном коде единица, выходящая за предел знаковых разрядов, отбрасывается.

Данный метод, при всей его простоте и наглядности, практического применения в ЭВМ не нашел. В основном, это связано с его большой избыточностью при кодировании данных и потерями времени при выполнении операции и последующей интерпретации результата.

Метод на основе логического преобразования сигналов межразрядных переносов

В настоящее время практически во всех компьютерах роль модифицированных кодов выполняют переносы, идущие в знаковый и из знакового разряда. Определение факта наличия переполнения выполняется практически одновременно с выполнением самой операции суммирования по следующей формуле:

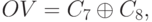
на примере восьмиразрядных операндов, где C₇ – перенос в старший (знаковый) разряд, а C₈ – перенос из знакового разряда.

Так при сложении операндов

произойдет переполнение разрядной сетки результата:

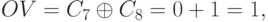
а при сложении операндов

нет, так как в данном случае: .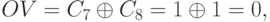

Такой подход требует использования всего лишь одного дополнительного элемента – "сумма по модулю два" – в сумматоре и практически не снижает его быстродействия.

Краткие итоги

В лекции рассмотрено представление чисел в прямом, обратном и дополнительном кодах. Особое внимание уделено дополнительному коду представления числа как наиболее распространенному в современных компьютерах. Показаны особенности алгебраического суммирования чисел в обратном и дополнительном кодах при различных сочетаниях операндов. Рассмотрены механизмы фиксации переполнения при выполнении операции алгебраического суммирования чисел.

Вопросы и задания

1. Как изображается знак числа при его кодировании? Возможно ли другое изображение знака числа? Сравните различные способы изображения знака.
2. В каком диапазоне размещаются числа с фиксированной запятой в прямом коде?
3. Как просуммировать числа, заданные в прямом коде без их перевода в обратный либо дополнительный код?
4. Какова методика получения обратного кода числа по его прямому коду?
5. Каковы недостатки алгебраического суммирования чисел в обратном коде?
6. Укажите самое большое и самое маленькое число в дополнительном коде, где под числовую часть отведено n разрядов.
7. Укажите правило суммирования чисел в обратном коде при отсутствии переполнения результата.
8. Какова методика получения дополнительного кода числа по его прямому коду?
9. В каком коде – прямом, обратном или дополнительном – можно представить больше чисел? Почему?
10. Запишите число (-3/8) в прямом, обратном и дополнительном кодах.
11. Укажите правило суммирования чисел в дополнительном коде при отсутствии переполнения результата.
12. В каком коде – обратном или дополнительном суммирование происходит быстрее? Почему?
13. Назовите основные методы фиксации переполнения при алгебраическом суммировании чисел в обратном и дополнительном кодах. Каковы их сравнительные достоинства и недостатки?
14. Какой из методов определения переполнения является самым быстродействующим? Какой из них требует наименьших дополнительных аппаратных затрат?
15. Система команд персональной ЭВМ на основе 16-разрядного микропроцессора может использовать как 8-, так и 16-разрядные операнды. Как в таком случае должка быть организована оперативная память и АЛУ такой ЭВМ, чтобы в ней можно было использовать модифицированный код для фиксации переполнения?