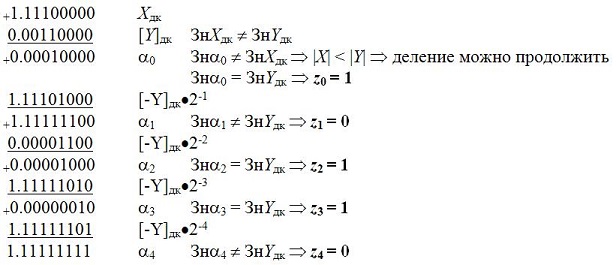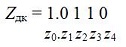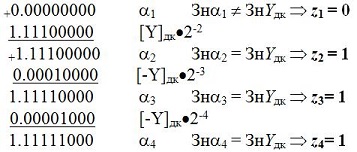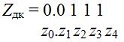| Россия, г. Москва |
Деление чисел с фиксированной запятой в прямом и дополнительном кодах
Деление чисел, заданных в дополнительном коде
Для чисел с фиксированной запятой, заданных в дополнительном коде, алгоритмы деления во многом совпадают с алгоритмами деления для чисел, заданных в прямом коде. Назовем лишь имеющиеся отличия:
- получаемый на начальном шаге деления нулевой остаток ?0 даёт возможность не только определить возможность продолжения деления для данного формата чисел, но и в случае удачного исхода определяет знак результата;
- получаемые при делении остатки позволяют определить очередную цифру частного непосредственно в дополнительном коде;
- нулевое значение получаемого на некотором шаге остатка не всегда служит основанием для прекращения деления;
- получаемые цифры результата не могут однозначно гарантировать, что результат последовательно получается с недостатком (речь идет об его абсолютной величине).
Деление со сдвигом и автоматическим восстановлением остатка
Как отмечалось выше, при любом алгоритме деления получение очередного остатка связано со сложение двух чисел разных знаков. Так как при делении чисел, заданных в дополнительном коде, знак результата получается автоматически в процессе деления, то основные формулы (9.1) и (9.2) несколько изменяются по сравнению с делением чисел, заданных в прямом коде:
![\alpha_0=\begin{cases}X_{ДК}+\left[Y\right]_{ДК},\text { если }ЗнX_{ДК}\neqЗн Y_{ДК}\\X_{ДК}+\left[-Y\right]_{ДК},\text { если }ЗнX_{ДК}=Зн Y_{ДК}\end{cases}](/sites/default/files/tex_cache/962699b5408ae9247728642013e51773.png)
Если Зн ?0 = Зн Xдк, то |X| ? |Y|. Следовательно, для чисел с фиксированной запятой Z = ?, и дальнейшее деление не имеет смысла.
Если Зн ?0 ? Зн Xдк, то очередные остатки при делении получаем по следующей рекуррентной формуле
![\alpha_{i+1}=\begin{cases}2\alpha_i+\left[Y\right]_{ДК},\text { если }Зн\alpha_i\neqЗн \left[Y\right]_{ДК}\\2\alpha_i+\left[-Y\right]_{ДК},\text { если }Зн\alpha_i=Зн \left[Y\right]_{ДК}\end{cases}](/sites/default/files/tex_cache/316515473e9e67193e49d9ffd76ce57e.png) |
( 9.5) |
Очередные разряды мантиссы результата, начиная с z0, вычисляются по формуле
![Z_{i ДК}=\begin{cases}0,\text{ если } Зн\alpha_i \neq Зн\left[Y\right]_{ДК}\\1,\text{ если } Зн\alpha_i = Зн\left[Y\right]_{ДК}\end{cases}](/sites/default/files/tex_cache/00ae5d40c053255b61ac17000f73dbdf.png) |
( 9.6) |
Пример 9.5
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 1.0111; Yдк = 1.0110.
Решение
Результат
Пример 9.6
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 1.0111; Yдк = 0.0110.
Решение
Деление со сдвигом делителя и автоматическим восстановлением остатка
Данный алгоритм деления сочетает в себе черты алгоритма деления со сдвигом и автоматическим восстановлением остатка для чисел, заданных в дополнительном коде, и алгоритма деления со сдвигом делителя для чисел, заданных в прямом коде.
Первый шаг проводится по формуле
![\alpha_0=\begin{cases}X_{ДК}+\left[Y\right]_{ДК},\text { если }ЗнX_{ДК}\neqЗн Y_{ДК}\\X_{ДК}+\left[-Y\right]_{ДК},\text { если }ЗнX_{ДК}=Зн Y_{ДК}\end{cases}](/sites/default/files/tex_cache/962699b5408ae9247728642013e51773.png)
На этом шаге, определяется, превышает ли модуль делимого модуль делителя и если нет, то определяется знак частного z0, на основании следующего выражения:
![Z_{i ДК}=\begin{cases}0,\text{ если } Зн\alpha_i \neq Зн\left[Y\right]_{ДК}\\1,\text{ если } Зн\alpha_i = Зн\left[Y\right]_{ДК}\end{cases}](/sites/default/files/tex_cache/00ae5d40c053255b61ac17000f73dbdf.png) |
( 9.10) |
Очередной остаток определяется следующим образом:
![\alpha_{i+1}=\begin{cases}\alpha_i+\left[ Y \right]_{ДК}\cdot 2^{-(i+1)}, \text{ если } Зн\alpha_i \neq Зн\left[Y\right]_{ДК}\\\alpha_i+\left[\left| -Y \right|\right]_{ДК}\cdot 2^{-(i+1)}, \text{ если } Зн\alpha_i = Зн\left[Y\right]_{ДК}\end{cases}](/sites/default/files/tex_cache/809bbc4595b78bda88de11a5ef5530cf.png) |
( 9.11) |
По соотношению знака очередного остатка и знака [Y]дк определяется очередная цифра частного согласно (9.10).
При построении арифметического устройства, использующего данный алгоритм деления, следует иметь в виду, что если мы не ориентируемся на укороченную разрядную сетку и связанные с этим механизмы коррекции результата после каждого шага вычислений, то из основных регистров необходимо иметь три 2n-разрядных регистров (для хранения делимого, делителя и остатков). Причем в число этих разрядов входит и знаковый разряд. Регистры делимого и делителя при первоначальной загрузке дополняются справа нулями. Кроме функции параллельной загрузки, регистр делителя должен иметь функцию сдвига вправо на один разряд.
Пример 9.7
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 1.1110; Yдк = 0.0011.
Решение
Результат
Пример 9.8
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 1.1100; Yдк = 1.1000.
Решение
На некотором шаге деления получили остаток, равный нулю. Стоит ли продолжать деление? При использовании алгоритмов деления чисел, заданных в прямом коде, деление в этом случае прекращалось, и остальные цифры результата записывались равными нулю. Но в этом случае мы получим результат
который явно не соответствует реальному.
Продолжим деление
Получаем окончательный результат:
то есть число, постепенно приближающееся к 2-1, что и следовало ожидать из анализа значений делимого и делителя.
Рассмотрим аналогичную ситуацию для случая отрицательного результата.
Пример 9.9
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 0.0010; Yдк = 1.1000.
Решение
Получили ситуацию, аналогичную предыдущему примеру – нулевой остаток. Дополнение получившихся разрядов результата (1.10) нулями приведет к тому, что модуль результата будет равен 2-1 (0.10002), в то время как он должен получиться равным 2-2 (0.01002), так как |X| = 0.0010 и |Y| = 0.1000. Поэтому деление в данном случае также необходимо продолжить до получения необходимого количества цифр частного. Не проводя соответствующих выкладок (они аналогичны предыдущим примерам), запишем следующий результат:
Таким образом, данный алгоритм деления предполагает, что при получении нулевого остатка на каком-либо шаге деление должно быть продолжено до получения необходимого количества цифр частного. В противном случае возможно существенное искажение результата.
Краткие итоги
В лекции представлены различные алгоритмы деления чисел с фиксированной запятой в прямом и дополнительном кодах. Рассмотрены схемотехнические особенности реализации каждого из алгоритмов деления. На примерах показаны некоторые особые случаи, возникающие в процессе деления.
Вопросы и задания
- Назовите основные способы деления чисел с фиксированной запятой в прямом и дополнительном кодах.
- Как связано количество разрядов частного с архитектурой конкретной ЭВМ?
- Как связан результат, получаемый при делении чисел, заданных в прямом коде, с истинным результатом: всегда превышает его, всегда меньше него, нельзя сказать однозначно?
- Какой из алгоритмов деления чисел, заданных в прямом коде, более экономичен с точки зрения используемого оборудования?
- Как формируется очередная цифра частного при получении нулевого остатка при делении чисел, заданных в прямом коде? Как в этом случае продолжается деление? Подтвердите ваше утверждение соответствующим примером.
- Какие операции сдвига можно совместить с другими операциями в алгоритме деления со сдвигом и автоматическим восстановлением остатка для чисел, заданных в прямом коде? Как такое совмещение отразится на времени выполнения операции деления и объеме используемого оборудования?
- Какой из алгоритмов деления чисел, заданных в прямом коде, позволяет быстрее получить конечный результат?
- Назовите схемотехнические элементы, необходимые для реализации блока деления чисел, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка и по алгоритму со сдвигом остатка и его автоматическим восстановлением.
- Какой из алгоритмов более быстродействующий и требует меньше аппаратных затрат: алгоритм деления чисел, заданных в прямом коде или заданных в дополнительном коде?