НОУ ИНТУИТ | Язык и библиотеки Haskell 98. Лекция 5: Объявления и связывания имен

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.09.2008 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 5 студентам

| Поделиться |

Поддержать программу

4.4 Вложенные объявления

Следующие объявления можно использовать в любом списке объявлений, включая верхний уровень модуля.

4.4.1 Сигнатуры типов

gendecl	$\to$	vars :: [context =>] type
vars	$\to$	var₁ , ..., var_n	(n >= 1)

Перевод:

общее-объявление	$\to$	список-переменных :: [контекст $\Rightarrow$ ] тип
список-переменых	$\to$	переменная₁ , ..., переменная_n	(n >= 1)

Сигнатура типа определяет типы для переменных, возможно по отношению к контексту. Сигнатура типа имеет вид:

v1, ..., vn :: cx => t

который эквивалентен утверждению v_i :: cx => t для каждого i от 1 до n. Каждая vi должна иметь связанное с ним значение в том же списке объявлений, который содержит сигнатуру типа, т.е. будет неправильным задать сигнатуру типа для переменной, связанной во внешней области видимости. Кроме того, будет неправильным задать более одной сигнатуры типа для одной переменной, даже если сигнатуры идентичны.

Как упомянуто в разделе "Объявления и связывания имен" , каждая переменная типа, появляющаяся в сигнатуре, находится под квантором всеобщности над сигнатурой, и, следовательно, область видимости переменной типа ограничена сигнатурой типа, которая ее содержит. Например, в следующих объявлениях

f :: a -> a
  f x = x :: a - неправильно

a в двух сигнатурах типа совершенно различны. Действительно, эти объявления содержат статическую ошибку, так как x не имеет тип forall a. A. (Тип x зависит от типа f ; в настоящее время в Haskell нет способа указать сигнатуру для переменной с зависимым типом, это раэъясняется в разделе "Объявления и связывания имен" .)

Если данная программа включает сигнатуру для переменной f, тогда каждое использование f трактуется как f, имеющая объявленный тип. Если тот же тип нельзя также вывести для определяемого вхождения f - возникнет статическая ошибка.

Если переменная f определена без соответствующей сигнатуры типа, тогда при использовании f вне его собственной группы объявлений (см. раздел "Объявления и связывания имен" ) переменная трактуется как имеющая соответствующий выведенный или основной тип . Тем не менее, для того чтобы гарантировать, что вывод типа еще возможен, определяемое вхождение и все использования f в пределах его группы объявлений должны иметь один и тот же мономорфный тип (из которого основной тип получается путем обобщения, описанного в разделе "Объявления и связывания имен" ).

Например, если мы определим

sqr x  =  x*x

тогда основным типом будет sqr :: forall a. Num a => a -> o a. Этот тип позволяет такое применение, как sqr 5 или sqr 0.1. Также правильным будет объявить более специализированный тип, например

sqr :: Int -> Int

но теперь такое применение, как sqr 0.1, будет неправильным. Такие сигнатуры типов, как

sqr :: (Num a, Num b) => a -> b     - неправильно
  sqr :: a -> a                       - неправильно

являются неправильными, поскольку они являются более общими, чем основной тип sqr.

Сигнатуры типов можно также использовать для того, чтобы обеспечить полиморфную рекурсию. Следующее определение является неправильным, зато показыает, как можно использовать сигнатуру типа для указания типа, который является более общим, чем тот, который был бы выведен:

data T a  =  K (T Int) (T a)

  f         :: T a -> a
  f (K x y) =  if f x == 1 then f y else undefined

Если мы уберем объявление сигнатуры, тип f будет выведен как T Int -> Int благодаря первому рекурсивному вызову, для которого аргументом f является T Int. Полиморфная рекурсия позволяет пользователю указать более общую сигнатуру типа T a -> a.

4.4.2 Infix-объявления

gendecl	$\to$	fixity [integer] ops
fixity	$\to$	infixl \| infixr \| infix
ops	$\to$	op₁ , ... , op_n	(n >= 1)
op	$\to$	varop \| conop

Перевод:

общеее-объявление	$\to$	ассоциативность [целый-литерал] список-операторов
ассоциативность	$\to$	infixl \| infixr \| infix
список-операторов	$\to$	оператор₁ , ... , оператор_n	(n >= 1)
оператор	$\to$	оператор-переменной\| оператор-конструктора

infix-объявление задает ассоциативность и приоритет (силу связывания) одного или более операторов. Целое число integer в infix-объявлении должно быть в диапазоне от 0 до 9. infix-объявление можно разместить всюду, где можно разместить сигнатуру типа. Как и сигнатура типа, infix-объявление задает свойства конкретного оператора. Так же, как и сигнатура типа, infix-объявление можно разместить только в той же последовательности объявлений, что и объявление самого оператора, и для любого оператора можно задать не более одного infix-объявления. (Методы класса являются небольшим исключением: их infix-объявления можно размещать в самом объявлении класса или на верхнем уровне.)

По способу ассоциативности операторы делятся на три вида: неассоциативные, левоассоциативные и правоассоциативные ( infix, infixl и infixr соответственно). По приоритету (силе связывания) операторы делятся на десять групп, в соответствии с уровнем приоритета от 0 до 9 включительно (уровень 0 связывает операнды наименее сильно, а уровень 9 - наиболее сильно). Если целое число integer не указано, оператору присваивается уровень приоритета 9. Любой оператор, для которого нет infix-объявления, считается объявленным infixl 9 (более подробную информацию об использовании infix-объявлений см. в разделе "Выражения" ). В п.4.4.3 и приоритеты операторов, определенных в Prelude.

Таблица 4.1.
Приоритет	Левоассоциативные операторы	Неассоциативные операторы	Правоассоциативные операторы
9	!!		.
8			^, ^^, **
7	*, /, 'div', 'mod', 'rem', 'quot'
6	+, -
5			:, ++
4		==, /=, <, <=, >, >=, elem', 'notElem'
3			&
2			\|
1	>>, >>=
0			$, $!, 'seq'

Приоритеты и ассоциативности операторов в Prelude

Ассоциативность является свойством конкретного объекта (конструктора или переменной), как и его тип; ассоциативность не является свойством имени объекта. Например,

module Bar( op ) where
    infixr 7 `op`
    op = ...
  
  module Foo where
    import qualified Bar
    infix 3 `op`
  
    a `op` b = (a `Bar.op` b) + 1
  
    f x = let
     p `op` q = (p `Foo.op` q) * 2
  in ...

Здесь 'Bar.op' - оператор с infixr 7, 'Foo.op' - оператор с infix 3, а оператор op во вложенном определении в правой части f имеет заданные по умолчанию infixl 9. (Свойства оператора 'op' во вложенном определении можно было бы также задать с помощью вложенного infix-объявления.)

4.4.3. Связывание имен в функциях и образцах

decl	$\to$	(funlhs \| pat⁰) rhs
funlhs	$\to$	var apat {apat }
	\|	patⁱ⁺¹ varop^(a,i) patⁱ⁺¹
	\|	lpatⁱ varop^(l,i) patⁱ⁺¹
	\|	patⁱ⁺¹ varop^(r,i) rpatⁱ
	\|	( funlhs ) apat {apat }
rhs	$\to$	= exp [where decls]
rhs	\|	gdrhs [where decls]
gdrhs	$\to$	gd = exp [gdrhs]
gd	$\to$	\| exp⁰

Перевод:

объявление	$\to$	(левая-часть-функции \| образец⁰) правая-часть
левая-часть-функции	$\to$	переменная такой-как-образец {такой-как-образец }
	\|	образецⁱ⁺¹ оператор-переменной^(a,i) образецⁱ⁺¹
	\|	левый-образецⁱ оператор-переменной^(l,i) образецⁱ⁺¹
	\|	образецⁱ⁺¹ оператор-переменной^(r,i) правый-образецⁱ
	\|	( левая-часть-функции ) такой-как-образец {такой-как-образец }
правая-часть	$\to$	= выражение [where список-объявлений]
правая-часть	\|	правая-часть-со-стражами [where список-объявлений]
правая-часть-со-стражами	$\to$	страж = выражение [правая-часть-со-стражами]
страж	$\to$	\| выражение⁰

Мы различаем два случая использования этого синтаксиса: связывание имен в образцах происходит, когда левой частью является pat⁰, в противном случае это связывание имен в функциях. Связывание имен может иметь место на верхнем уровне модуля или в пределах конструкций where или let.

4.4.3.1 Связывание имен в функциях

Связывание имен в функции связывает переменную со значением функции. Связывание имен в функции для переменной x в общем виде выглядит так:

x  p11 ... p1k  match1
...
x  pn1 ... pnk  matchn

где каждое pij - образец, а каждое matchi в общем виде выглядит так:

= ei where { declsi }

или

\| g_i1	= e_i1
...
\| g_imi	= e_imi
	where { decls_i }

n>=1, 1 >= i >= n, m_i>=1. Первый из двух вариантов рассматривается как краткая запись для особого случая второго варианта, а именно:

| True = ei where { declsi }

Отметим, что все инструкции, определяющие функцию, должны следовать непосредственно друг за другом, и число образцов в каждой инструкции должно быть одно и то же. Набор образцов, соответствующий каждому сопоставлению, должен быть линейным: никакая переменная не может появиться во всем наборе более одного раза.

Для связывания значений функций с инфиксными операторами имеется альтернативный синтаксис. Например, все эти три определения функции эквивалентны:

plus x y z = x+y+z
  x `plus` y = \ z -> x+y+z
  (x `plus` y) z = x+y+z

Трансляция:

Связывание имен для функций в общем виде семантически эквивалентно уравнению (т.е. простому связыванию имен в образцах):

x = \ x₁ ... x_k -> case (x₁, ..., x_k) of

(p₁₁, ..., p_1k) match₁

...

(pn₁, ..., p_nk) match_n

где x_i - новые идентификаторы

4.4.3.2 Связывание имен в образцах

Связывание имен в образцах связывает переменные со значениями. Простое связывание имен в образцах имеет вид p = e. Образец p "лениво" сопоставляется значению, как неопровержимый образец, как если бы впереди него был указана 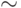$\sim$ (см. трансляцию в разделе "Выражения" ).

В общем виде связывание имен в образцах выглядит так: p match, где match имеет ту же структуру, что для описанного выше связывания имен в функциях, другими словами, связывание имен в образцах имеет вид:

p	\| g₁	= e₁
	\| g₂	= e₂
	…
	\| g_m	= e_m
	where { decls }

Трансляция:

Описанное выше связывание имен в образцах семантически эквивалентно этому простому связыванию имен в образцах:

p	=	let decls in
		if g₁ then e₁ else
		if g₂ then e₂ else
		...
		if g_m then e_m else error "Несопоставимый образец"

Замечание о синтаксисе

Обычно просто отличить, является ли связывание имен связыванием имен в образце или в функции, но наличие n+k -образцов иногда сбивает с толку. Рассмотрим четыре примера:

x + 1 = ... - Связывание имен в функции, определяет (+)
- Эквивалентно   (+) x 1 = ...

  (x + 1) = ... - Связывание имен в образце, определяет x

  (x + 1) * y = ... - Связывание имен в функции, определяет (*)
- Эквивалентно   (*) (x+1) y = ...

  (x + 1) y = ... - Связывание имен в функции, определяет (+)
- Эквивалентно   (+) x 1 y = ...

Первые два связывания имен можно различить, потому что связывание имен в образце имеет в левой части pat⁰, а не pat, связывание имен в первом примере не может быть n+k -образцом без скобок.

Дальше >>

Язык и библиотеки Haskell 98

Язык и библиотеки Haskell 98

Объявления и связывания имен

4.4 Вложенные объявления

4.4.1 Сигнатуры типов

4.4.2 Infix-объявления

Приоритеты и ассоциативности операторов в Prelude

4.4.3. Связывание имен в функциях и образцах

4.4.3.1 Связывание имен в функциях

4.4.3.2 Связывание имен в образцах

Замечание о синтаксисе

Вопросы и ответы

Студенты

Авторизоваться

Язык и библиотеки Haskell 98

Язык и библиотеки Haskell 98

Объявления и связывания имен

4.4 Вложенные объявления

4.4.1 Сигнатуры типов

4.4.2 Infix-объявления

Приоритеты и ассоциативности операторов в Prelude

4.4.3. Связывание имен в функциях и образцах

4.4.3.1 Связывание имен в функциях

4.4.3.2 Связывание имен в образцах

Замечание о синтаксисе

Вопросы и ответы

Студенты