Параллельные методы сортировки
9.5.2.3. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного варианта быстрой сортировки производились при тех же условиях, что и ранее выполненные эксперименты (см. п. 9.3.6).
Результаты вычислительных экспериментов приведены в табл. 9.6. Эксперименты проводились с использованием двух и четырех процессоров. Время указано в секундах.
| Количество элементов | Последовательный алгоритм | Параллельный алгоритм | |||
|---|---|---|---|---|---|
| 2 процессора | 4 процессора | ||||
| Время | Ускорение | Время | Ускорение | ||
| 10000 | 0,001422 | 0,001521 | 0,934911 | 0,003434 | 0,414094 |
| 20000 | 0,002991 | 0,002234 | 1,338854 | 0,004094 | 0,730581 |
| 30000 | 0,004612 | 0,003080 | 1,497403 | 0,005088 | 0,906447 |
| 40000 | 0,006297 | 0,004363 | 1,443273 | 0,005906 | 1,066204 |
| 50000 | 0,008014 | 0,005486 | 1,460809 | 0,006635 | 1,207837 |
Как можно заметить по результатам вычислительных экспериментов, параллельный алгоритм быстрой сортировки уже позволяет получить ускорение при решении задачи упорядочивания данных.
Сравнение времени выполнения эксперимента 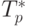 и
теоретической оценки Tp из (9.11)
приведено в таблице 9.7 и на
рис. 9.8.
и
теоретической оценки Tp из (9.11)
приведено в таблице 9.7 и на
рис. 9.8.
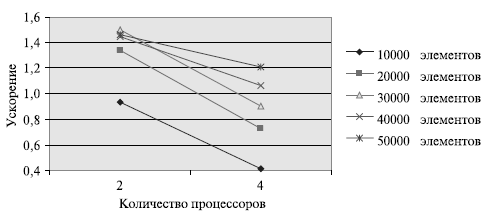
Рис. 9.7. Зависимость ускорения от количества процессоров при выполнении параллельного алгоритма быстрой сортировки
| Количество элементов | Параллельный алгоритм | |||
|---|---|---|---|---|
| 2 процессора | 4 процессора | |||
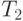 |
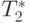 |
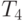 |
 |
|
| 10000 | 0,001280 | 0,001521 | 0,001735 | 0,003434 |
| 20000 | 0,002265 | 0,002234 | 0,002321 | 0,004094 |
| 30000 | 0,003289 | 0,003080 | 0,002928 | 0,005088 |
| 40000 | 0,004338 | 0,004363 | 0,003547 | 0,005906 |
| 50000 | 0,005407 | 0,005486 | 0,004175 | 0,006635 |
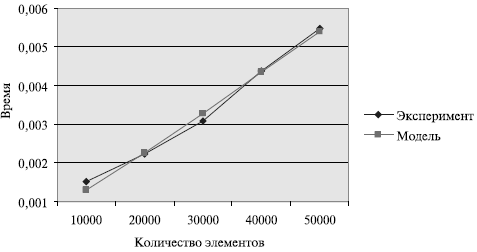
Рис. 9.8. График зависимости экспериментального и теоретического времени проведения эксперимента на двух процессорах от объема исходных данных
9.5.3. Обобщенный алгоритм быстрой сортировки
В обобщенном алгоритме быстрой сортировки ( the HyperQuickSort algorithm ) в дополнение к обычному методу быстрой сортировки предлагается конкретный способ выбора ведущих элементов. Суть предложения состоит в том, что сортировка располагаемых на процессорах блоков происходит в самом начале выполнения вычислений. Кроме того, для поддержки упорядоченности в ходе вычислений процессоры должны выполнять операции слияния частей блоков, получаемых после разделения. Как результат, в силу упорядоченности блоков, при выполнении алгоритма быстрой сортировки в качестве ведущего элемента целесообразнее будет выбирать средний элемент какого-либо блока (например, на первом процессоре вычислительной системы). Выбираемый подобным образом ведущий элемент в отдельных случаях может оказаться более близким к реальному среднему значению всего сортируемого набора, чем какое-либо другое произвольно выбранное значение.
Все остальные действия в новом рассматриваемом алгоритме выполняются в соответствии с обычным методом быстрой сортировки. Более подробное описание данного способа распараллеливания быстрой сортировки может быть получено, например, в [ [ 63 ] ].
При анализе эффективности обобщенного алгоритма можно воспользоваться соотношением (9.11). Следует только учесть, что на каждой итерации метода теперь выполняется операция слияния частей блоков (будем, как и ранее, предполагать, что их размер одинаков и равен (n/p)/2). Кроме того, в силу упорядоченности блоков может быть усовершенствована процедура деления – вместо перебора всех элементов блока теперь достаточно будет выполнить для ведущего элемента бинарный поиск в блоке. С учетом всех высказанных замечаний трудоемкость обобщенного алгоритма быстрой сортировки может быть выражена при помощи следующего выражения:
![T_p=[(n/p)\log_2(n/p)+(\log_2(n/p)+(n/p))\log_2 p]\tau +
(log_2 p)^2 (\alpha+w/ \beta) + \log_2 p(\alpha+w(n/2p)/ \beta)](/sites/default/files/tex_cache/909f9ddd20227afd946c2b3ea6386653.png) |
( 9.12) |

