Параллельные методы сортировки
9.5. Быстрая сортировка
9.5.1. Последовательный алгоритм
При общем рассмотрении алгоритма быстрой сортировки ( the quick sort algorithm ), предложенной Хоаром ( C.A.R. Hoare ), прежде всего следует отметить, что этот метод основывается на последовательном разделении сортируемого набора данных на блоки меньшего размера таким образом, что между значениями разных блоков обеспечивается отношение упорядоченности (для любой пары блоков все значения одного из этих блоков не превышают значений другого блока). На первой итерации метода осуществляется деление исходного набора данных на первые две части – для организации такого деления выбирается некоторый ведущий элемент и все значения набора, меньшие ведущего элемента, переносятся в первый формируемый блок, все остальные значения образуют второй блок набора. На второй итерации сортировки описанные правила применяются рекурсивно для обоих сформированных блоков и т.д. При надлежащем выборе ведущих элементов после выполнения log2n итераций исходный массив данных оказывается упорядоченным. Более подробное изложение метода может быть получено, например, в [ [ 26 ] , [ 50 ] ].
Эффективность быстрой сортировки в значительной степени
определяется правильностью выбора ведущих элементов при
формировании блоков. В худшем случае трудоемкость метода имеет
тот же порядок сложности, что и пузырьковая сортировка (т.е. T1~n2 ). При оптимальном выборе ведущих элементов, когда
разделение каждого блока происходит на равные по размеру части,
трудоемкость алгоритма совпадает с быстродействием наиболее
эффективных способов сортировки 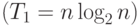 . В среднем случае
количество операций, выполняемых алгоритмом быстрой сортировки,
определяется выражением (см., например, [
[
26
]
,
[
50
]
]):
. В среднем случае
количество операций, выполняемых алгоритмом быстрой сортировки,
определяется выражением (см., например, [
[
26
]
,
[
50
]
]):
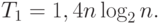
Общая схема алгоритма быстрой сортировки может быть представлена в следующем виде (в качестве ведущего элемента выбирается первый элемент упорядочиваемого набора данных).
Алгоритм 9.5. Последовательный алгоритм быстрой сортировки
// Алгоритм 9.5
// Последовательный алгоритм быстрой сортировки
void QuickSort(double A[], int i1, int i2) {
if (i1 < i2) {
double pivot = A[i1];
int is = i1;
for (int i = i1 + 1; i < i2; i++)
if (A[i] Ј pivot) {
is = is + 1;
swap(A[is], A[i]);
}
swap(A[i1], A[is]);
QuickSort(A, i1, is);
QuickSort(A, is + 1, i2);
}
}9.5.2. Параллельный алгоритм быстрой сортировки
9.5.2.1. Организация параллельных вычислений
Параллельное обобщение алгоритма быстрой сортировки (см., например, [63]) наиболее простым способом может быть получено, если топология коммуникационной сети может быть эффективно представлена в виде N -мерного гиперкуба (т.е. p=2N ). Пусть, как и ранее, исходный набор данных распределен между процессорами блоками одинакового размера n/p ; результирующее расположение блоков должно соответствовать нумерации процессоров гиперкуба. Возможный способ выполнения первой итерации параллельного метода при таких условиях может состоять в следующем:
- выбрать каким-либо образом ведущий элемент и разослать его по всем процессорам системы (например, в качестве ведущего элемента можно взять среднее арифметическое элементов, расположенных на выбранном ведущем процессоре);
- разделить на каждом процессоре имеющийся блок данных на две части с использованием полученного ведущего элемента;
- образовать пары процессоров, для которых битовое представление номеров отличается только в позиции N, и осуществить взаимообмен данными между этими процессорами.
В результате выполнения такой итерации сортировки исходный набор оказывается разделенным на две части, одна из которых (со значениями меньшими, чем значение ведущего элемента) располагается на процессорах, в битовом представлении номеров которых бит N равен 0. Таких процессоров всего p/2, и, таким образом, исходный N -мерный гиперкуб также оказывается разделенным на два гиперкуба размерности N-1. К этим подгиперкубам, в свою очередь, может быть параллельно применена описанная выше процедура. После N -кратного повторения подобных итераций для завершения сортировки достаточно упорядочить блоки данных, получившиеся на каждом отдельном процессоре вычислительной системы.
Для пояснения на рис. 9.6 представлен пример упорядочивания данных при n=16, p=4 (т.е. блок каждого процессора содержит 4 элемента). На этом рисунке процессоры изображены в виде прямоугольников, внутри которых показано содержимое упорядочиваемых блоков данных; значения блоков приводятся в начале и при завершении каждой итерации сортировки. Взаимодействующие пары процессоров соединены двунаправленными стрелками. Для разделения данных выбирались наилучшие значения ведущих элементов: на первой итерации для всех процессоров использовалось значение 0, на второй итерации для пары процессоров 0, 1 ведущий элемент равен -5, для пары процессоров 2, 3 это значение было принято равным 4.

Рис. 9.6. Пример упорядочивания данных параллельным методом быстрой сортировки (без результатов локальной сортировки блоков)
Как и ранее, в качестве базовой подзадачи для организации параллельных вычислений может быть выбрана операция "сравнить и разделить", а количество подзадач совпадает с числом используемых процессоров. Распределение подзадач по процессорам должно производиться с учетом возможности эффективного выполнения алгоритма при представлении топологии сети передачи данных в виде гиперкуба.
9.5.2.2. Анализ эффективности
Оценим трудоемкость рассмотренного параллельного метода. Пусть у нас имеется N -мерный гиперкуб, состоящий из p=2N процессоров, где p<n.
Эффективность параллельного метода быстрой сортировки, как и в последовательном варианте, во многом зависит от правильности выбора значений ведущих элементов. Определение общего правила для выбора этих значений представляется затруднительным. Сложность такого выбора может быть снижена, если выполнить упорядочение локальных блоков процессоров перед началом сортировки и обеспечить однородное распределение сортируемых данных между процессорами вычислительной системы.
Определим вначале вычислительную сложность алгоритма сортировки. На каждой из log2p итераций сортировки каждый процессор осуществляет деление блока относительно ведущего элемента, сложность этой операции составляет n/p операций (будем предполагать, что на каждой итерации сортировки каждый блок делится на равные по размеру части).
При завершении вычислений процессор выполняет сортировку своих блоков, что может быть выполнено при использовании быстрых алгоритмов за (n/p)log2(n/p) операций.
Таким образом, общее время вычислений параллельного алгоритма быстрой сортировки составляет
![T_p(calc)=[(n/p)\log_2 p+(n/p)\log_2(n/p)]\tau ,](/sites/default/files/tex_cache/e225a7966effab7d2f3a78b4e3e6c48d.png) |
( 9.8) |
 есть время выполнения базовой операции перестановки.
есть время выполнения базовой операции перестановки.Рассмотрим теперь сложность выполняемых коммуникационных операций. Общее количество межпроцессорных обменов для рассылки ведущего элемента на N -мерном гиперкубе может быть ограничено оценкой
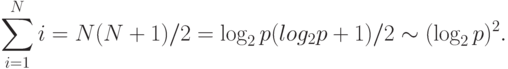 |
( 9.9) |
При используемых предположениях (выбор ведущих элементов осуществляется наилучшим образом) количество итераций алгоритма равно log2p, а объем передаваемых данных между процессорами всегда равен половине блока, т.е. величине (n/p)/2. При таких условиях коммуникационная сложность параллельного алгоритма быстрой сортировки определяется при помощи соотношения:
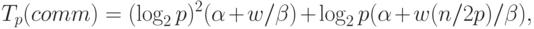 |
( 9.10) |
 – латентность,
– латентность,  – пропускная способность сети,
а w есть размер элемента набора в байтах.
– пропускная способность сети,
а w есть размер элемента набора в байтах.С учетом всех полученных соотношений общая трудоемкость алгоритма оказывается равной
![T_p=[(n/p)\log_2 p+(n/p)\log_2(n/p)]\tau+
(log_2 p)^2(\alpha+w/ \beta) + \log_2 p(\alpha+w(n/2p)/ \beta).](/sites/default/files/tex_cache/acc14eb0dd0920e456af600117ef5252.png) |
( 9.11) |

