| Россия, г. Туймазы |
Электронные платежные системы на основе цифровых денег
8.3.4. Неотслеживаемость дебитора и кредитора
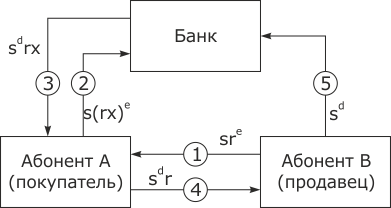
Технология, основанная на двойном затемнении, и соответствующие обмены показаны на рис. 8.5.
Взаимная неотслеживаемость обеспечивается за счет слияния двух предыдущих схем.
Шаг 1. Абонент В формирует "полуфабрикат" цифровой купюры, затем посылает его абоненту А.
Шаг 2. Абонент А после получения купюры, произведенной клиентом В, добавляет другой затемняющий множитель, выбирая случайное число x, равномерно распределенное между 1 и (N – 1). Купюра посылается в банк для постановки слепой подписи в виде:
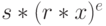 .
.
Шаг 3. Банк подписывает вслепую полученную купюру и возвращает ее абоненту А.
Шаг 4. Абонент А снимает свой затемняющий множитель и отправляет полученное сообщение абоненту В.
Шаг 5. Абонент В снимает свой затемняющий множитель и получает полноценную цифровую купюру, которую предъявляет банку.
Другой путь обеспечения взаимной неотслеживаемости - это комбинация двух простейших случаев неотслеживаемости дебитора и кредитора и приглашения доверенной третьей стороны, которая включается между участниками. Клиент общается с третьей стороной, используя протокол, обеспечивающий его неотслеживаемость. Доверенная третья сторона ретранслирует платеж продавцу в соответствии с правилом неотслеживаемости кредитора. Банк может быть этой третьей стороной, даже несмотря на то, что в этой роли он не может отследить ни покупателя, ни продавца.
8.3.5. Номинал (достоинство) цифровых банкнот
Рассмотрим двоичное представление стоимости купюры, показанное на рис. 8.6.
В этом случае номинал купюры может принимать любое значение от 1 до 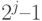 . Каждому разряду соответствует одно из простых чисел, делителей банковской открытой экспоненты криптосистемы RSA.
. Каждому разряду соответствует одно из простых чисел, делителей банковской открытой экспоненты криптосистемы RSA.
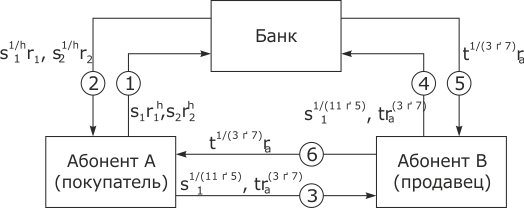
Таким образом, для представления стоимости, равной 1, используется экспонента, равная 3. Аналогично стоимость, равная 2 в десятичном представлении (или 10 в двоичном), соотносится с открытой экспонентой, равной 5; стоимость, равная 4 в десятичном представлении (или 100 в двоичном), соотносится с открытой экспонентой, равной 7 и т.д. В результате при использовании открытой экспоненты 11 × 7 × 5 × 3 купюра с 4-разрядным кодом стоимости может иметь номинал, принимающий любое значение от 1 до 15 условных единиц (между 0001 и 1111 в двоичном представлении). Следующий пример, схематично отраженный на рис. 8.7, показывает, как при вышеописанной схеме представления достоинства купюры решается проблема обмена.
Предположим, стоимость представлена 4-разрядным двоичным кодом. Допустим, клиент хочет приобрести две цифровые купюры, каждая достоинством 15 условных единиц. Каждая купюра имеет свой собственный серийный номер, соответственно 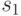 и
и 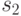 . Соответствующие затемняющие множители равны
. Соответствующие затемняющие множители равны 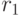 и
и 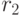 .
.
Банковская открытая экспонента для представления купюры максимального достоинства равна
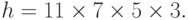
Шаг 1. Абонент А производит две купюры, скрывая их номера с использованием затемняющих множителей, и посылает их в банк для простановки слепой подписи. Сообщение, посылаемое в банк, суть конкатенация двух запросов:
Шаг 2. Банк снимает со счета абонента А соответствующую сумму (30 условных единиц), подписывает вслепую купюры и затем возвращает составное сообщение
Инверсия 1 / h суть банковская секретная экспонента, которая вычисляется по формуле
![h \times (1 / h) = 1 mod [ (p – 1) (q – 1) ].](/sites/default/files/tex_cache/a009b571374c48929bee59675823b0af.png)
Эта экспонента, также как и открытая, определяет общую стоимость купюры.
Шаг 3. При выполнении платежа первой купюрой за товар (или услугу) стоимостью 10 единиц (двоичное представление 1010) абонент А использует экспоненту  в своем запросе. Он составляет сообщение для отправки абоненту В (продавцу) в следующем виде:
в своем запросе. Он составляет сообщение для отправки абоненту В (продавцу) в следующем виде:
Для получения "сдачи" абонент А становится неотслеживаемым кредитором для банка в соответствии с вышеописанным протоколом. Абоненту А необходимо удержать остаток в 5 условных единиц. Для этого он формирует число t (по сути вторую цифровую купюру) и скрывает его с помощью затемняющего множителя 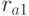 , зашифрованного с использованием экспоненты
, зашифрованного с использованием экспоненты  , соответствующей сумме в 5 условных единиц:
, соответствующей сумме в 5 условных единиц:
Покупатель (абонент А) желает заплатить продавцу (абоненту В) 10 условных единиц. Для этого абонент А формирует составное сообщение
и посылает его абоненту В.
Шаг 4. Абонент В пересылает это сообщение банку.
Шаг 5. Банк возвращает абоненту В купюру t, подписанную с использованием экспоненты 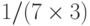 :
:
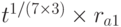 .
.
Шаг 6. Абонент В пересылает это сообщение (по сути, сдачу) абоненту А. Абонент А снимает действие затемняющего множителя и получает подписанную банком купюру достоинством 5 условных единиц:
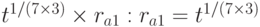 .
.
Рассмотрим еще один возможный вид платежа.
Шаг 1. Допустим, второй платеж осуществляется на сумму в 12 условных единиц (двоичное представление 1100), открытая экспонента в этом случае равна 11 × 7. Составное сообщение от А к В с использованием затемняющего множителя  в этом случае будет иметь вид:
в этом случае будет иметь вид:
Шаг 2. Абонент В пересылает это сообщение банку.
Шаг 3. Банк возвращает абоненту В купюру t, подписанную с использованием экспоненты 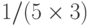 :
:
 .
.
Шаг 4. Абонент В пересылает это сообщение абоненту А. Абонент А снимает действие затемняющего множителя и получает подписанную банком купюру с "накопленным" достоинством (5 + 3) условных единиц:
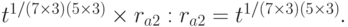
Шаг 5. В транзакции депозита абонент А может положить накопленную сумму на свой счет. Для этого он посылает в банк сообщение:
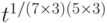 ,
,
указывая при этом значение накопленной суммы.
Шаг 6. Банк проверяет, не использовалась ли ранее купюра-накопитель, вычисляет накопленную сумму и переводит ее на счет абонента А.
8.3.6. Обнаружение подделки
Изготовление фальшивых банкнот - основной способ подделки обычных бумажных денег. Для предотвращения этого принимаются специальные меры (применение бумаги высокого качества, вставка магнитных полос, водяных знаков и пр.), существенно затрудняющие изготовление фальшивок. В случае цифровых денег их копирование осуществить очень легко, для этого достаточно скопировать файл с соответствующей информацией. Иначе говоря, появляется проблема повторного использования. Даже если банк сможет отличить подлинную купюру от фальшивой по серийным номерам, он не в состоянии идентифицировать нарушителя.
Следующий алгоритм, предложенный Д. Чаумом, определяет мошенника без идентификации подлинного дебитора.
Формирование цифровой купюры. Рассмотрим дебитора (В), который имеет в банке счет u, с которым связан счетчик v.
Шаг 1. Дебитор формирует k затемненных сообщений:
При этом 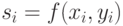 ,
,
Независимые переменные  ,
,  и
и 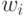 равномерно распределены в интервале
равномерно распределены в интервале ![[1, (N – 1)]](/sites/default/files/tex_cache/e77579701875c5d646fe114bf793dd8f.png) . Эти k сообщений отправляются банку в качестве кандидатов на получение на их основе цифровых купюр. Функции f ( ) и g ( ) - функции двух аргументов, не имеющие коллизий, иначе говоря, каждой паре входных значений соответствует определенное значение результата.
. Эти k сообщений отправляются банку в качестве кандидатов на получение на их основе цифровых купюр. Функции f ( ) и g ( ) - функции двух аргументов, не имеющие коллизий, иначе говоря, каждой паре входных значений соответствует определенное значение результата.
Шаг 2. Банк случайным образом выбирает k / 2 кандидатов для проверки и просит дебитора предъявить соответствующие переменные  ,
,  ,
,  и
и 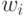 . Пусть R - набор этих k / 2 кандидатов.
. Пусть R - набор этих k / 2 кандидатов.
Шаг 3. Если банк завершил все проверки и не обнаружил никаких нарушений, он отправляет обратно произведение k / 2 кандидатов, подписанных своим секретным ключом d:
Шаг 4. Банк снимает со счета дебитора соответствующую сумму.
Шаг 5. Как и в предыдущих схемах, дебитор удаляет затемняющие множители и получает цифровую купюру в виде:
Вероятность обнаружения мошенничества, очевидно, будет зависеть от числа k (по сути, параметра безопасности) и частоты фактов обмана.
Покупка. Когда дебитор посылает продавцу цифровую купюру, последний начинает проверочную процедуру для предотвращения мошенничества. Эта процедура состоит из последовательных действий.
Шаг 1. Продавец выбирает случайную двоичную строку:
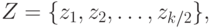
Шаг 2. Для всех элементов 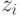 строки Z,
строки Z,
если 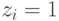 , продавец просит клиента послать сообщение:
, продавец просит клиента послать сообщение:
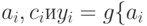
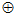
![[u || (v + i)], w_i\}](/sites/default/files/tex_cache/e378df2a36ff86bf3c59692d23e95e83.png) ;
;
если  , продавец просит клиента послать сообщение:
, продавец просит клиента послать сообщение:
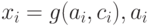
![[u || (v + i)]](/sites/default/files/tex_cache/9ebf6c72608ce29abb101deddb4f4030.png) и
и 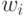 .
.
Шаг 3. Продавец проверяет, имеет ли полученная цифровая купюра требуемый формат, а затем посылает купюру, строку Z и ответы клиента банку с запросом финансового расчета.
8.4. DigiCash
Примером платежной системы, использующей цифровые наличные, является DigiCash.
В 1990 г. Д. Чаум организовал в Нидерландах и США коммерческую фирму DigiCash. Mark Twain Bank Сент-Луиса согласился поддерживать конвертацию цифровой наличности в доллары США. Он поддерживал специальный счет для принятия сумм, циркулирующих в цифровом виде до операций депонирования на обычные банковские счета кредиторов.
Одноименная платежная система DigiCash создавалась в рамках европейского проекта Esprit. При этом целью являлось обеспечение цифрового денежного обращения с использованием идей Д. Чаума и его команды. DigiCash использует цифровую наличность, называемую eCash, заменяющую обычные монеты и купюры и обеспечивающую анонимность платежей и неотслеживаемость.
ECash - это виртуальная валюта, предназначенная для оплаты товаров и услуг через компьютерные сети. В рамках системы DigiCash пользователь формирует eCash и посылает их в банк на подпись. Цифровые деньги, полученные из банка, в дальнейшем хранятся на жестком диске клиента, куда с помощью клиентского программного обеспечения "закачиваются" со счета клиента в некоем виртуальном банке (digital bank), созданном компанией DigiCash в сети Интернет. Для пересылки eCash необходимо соединение между продавцом и покупателем в режиме он-лайн, предполагался также выпуск ПО, позволяющего проводить платежи по электронной почте. Цифровые деньги могут быть истрачены в любом торговом предприятии, принимающем их к оплате, причем никаких сведений о клиенте продавцу не требуется. Таким образом, eCash представляет собой полный аналог наличных для "электронного рынка". Банк к своей роли посредника в финансовых расчетах может добавить роль доверенной третьей стороны. На рис. 8.8 показаны отношения, которые DigiCash устанавливает между участниками транзакций.
Сумма, пересылаемая от покупателя к продавцу, защищается криптографическими методами, а для загрузки цифровых денег на компьютер клиента нужно ввести пароль, известный только владельцу счета в виртуальном банке, с которого происходит загрузка.
Пользователь (клиент А) загружает ПО, которое позволяет браузеру сохранять деньги клиента, следить за расходами и проверять временные отметки. Во время регистрации клиент получает все открытые ключи, которые будут использоваться при создании цифровых купюр различного достоинства. Аналогично клиент В (продавец) загружает и регистрирует свое ПО для приема электронных платежей, для взаимодействия с покупателями и банком. Оба абонента должны иметь счета в банке.
С целью обеспечения аутентичности обменов участники взаимодействия используют свои секретные ключи для подписывания сообщений. Для обеспечения конфиденциальности участники взаимодействия используют секретные сеансовые ключи, которые в свою очередь будут зашифрованы банковским открытым ключом.
Для защиты от сбоев (терминальных или сетевых) банк может хранить копии n последних запросов каждого клиента (например, n = 16). Это создает условия для восстановления информации в случае неполадок в работе.
Клиент eCash. Клиент eCash может быть установлен на любом компьютере, имеющем полномасштабный доступ к Интернету. Установка клиента не требует никаких особых навыков. Пользовательский интерфейс клиента eCash представляет собой окно (в терминах интерфейса MS Windows), постоянно находящееся "наверху" рабочего пространства (desktop). В "свернутом" виде это окно содержит лишь указание на количество находящейся "на руках" у пользователя цифровой наличности, а также может содержать пиктограмму и (или) окно микроанимации для указания на осуществляемые клиентом в настоящий момент действия. В "развернутом" виде окно содержит пять кнопок.
- Связь с банком(eCash Withdraw/Deposit). При нажатии этой кнопки открывается окно, и пользователь должен указать тип транзакции (снятие "наличных" со счета либо помещение "наличных" на счет) и сумму.
- Проведение платежа (eCash Payment). Эта кнопка открывает окно, в котором задаются характеристики проводимого "вручную" платежа. Следует отметить, что в большинстве случаев связь двух клиентов осуществляется в автоматическом режиме: покупатель выбирает нужный ему товар, пролистывая страницы гипертекста обычным браузером, а эта программа просмотра вызывает клиента eCash, и от пользователя требуется лишь подтвердить свою готовность совершить покупку (см. пример ниже). Однако некоторые версии позволяют осуществить либо принять платеж непосредственно из eCash, открывающего для этого сеанс IP-связи с другим клиентом (который также должен находиться на компьютере в режиме он-лайн), и даже по электронной почте. В открываемом окне можно указать имя счета контрагента (для платежей по электронной почте), имя хост-компьютера (для платежа по IP), сумму и снабдить платеж примечанием.
- Просмотр списка осуществленных платежей (eCash Payment Log). При нажатии этой кнопки открывается окно, позволяющее просмотреть список осуществленных и принятых платежей, включая информацию об имени счета контрагента и сумме платежа.
- Состояние клиента (eCash Status). Эта кнопка открывает окно с информацией об установленном клиенте, включая баланс счета в банке, адрес банка и имя счета. Нажатие еще одной кнопки позволяет взглянуть на имеющиеся "на руках" цифровые монеты.
- Пользовательские установки (eCash Preferences). Открывает окно, в котором устанавливаются пользовательские параметры, включая деноминацию валюты, метод соединения с банком и некоторые другие.
8.5 Перспективы
Можно выделить три группы обсуждаемых последствий широкого принятия цифровой наличности в качестве платежного инструмента.
- Увеличение скорости обращения денежной массы.
- Увеличение скорости исполнения принятых экономическими агентами решений о перемещении средств.При этом следует учитывать, что критическим является не увеличение скорости принятия и исполнения решений как таковой, а соотношение между ней и скоростью реагирования на принятые решения систем, формирующих финансовые индексы. Проблема заключается, таким образом, скорее в технологическом отставании традиционных банковских, финансовых и информационных систем.
- Изменение роли банков в национальных и мировой финансовых системах.Надежность, доступность и дешевизна современных электронных коммуникаций - одна из важнейших составляющих возможного распространения цифровой наличности. В реализации любой крупной системы наличных электронных платежей ключевое место будет принадлежать фирмам, специализирующимся на обеспечении связи, - телефонным компаниям и поставщикам сетевых услуг. Есть мнение, что в случае разворачивания систем цифровой наличности коммерческие банки могут потерять свое центральное место в денежно-финансовой системе.




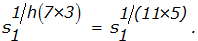

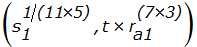

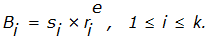

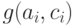 ;
;
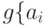

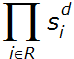
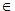
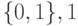
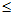

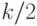 .
.