|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Сети очередей
Предположение независимости Клейнрока
В реальной сети передачи данных пакеты будут иметь одну и ту же постоянную длину и поэтому одно и то же время обслуживания на всех линиях связи и узлах с равной скоростью обслуживания. Теория сети очередей принимает, что пакет (клиент) производит выбор нового времени обслуживания на каждом узле. Это - необходимое предположение для мультипликативной формы. Такое предположение было впервые исследовано Клейнроком (1964 [65] ), и, оказывается, оно дает хорошее приближение к практике.
Сети очередей с одиночными цепочками
Мы интересуемся вероятностями состояния, определенными  , где
, где  - число клиентов в узле
- число клиентов в узле  .
.
Расчет открытых сетей прост. Сначала мы решаем уравнение равновесия потока (14.5) и получаем объединенную интенсивность прибытия к каждому узлу ( 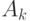 ). Комбинируя интенсивности прибытия с распределением времени обслуживания (
). Комбинируя интенсивности прибытия с распределением времени обслуживания ( 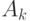 ), получаем предложенную нагрузку
), получаем предложенную нагрузку 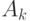 на каждом узле и затем, рассматривая Эрланговскую систему с ожиданием, находим вероятности состояния для каждого узла.
на каждом узле и затем, рассматривая Эрланговскую систему с ожиданием, находим вероятности состояния для каждого узла.
Алгоритм свертывания для закрытой сети очередей
Исследование закрытых сетей с очередями намного сложнее, чем открытых. Мы знаем только относительную нагрузку на каждом узле, а не абсолютную нагрузку, то есть c 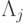 получена, но
получена, но  неизвестно. Можно получить относительную нормализованную вероятность состояния. Наконец, нормализуя, мы получим нормализованные вероятности состояния. К сожалению, нормализация подразумевает, что необходимо суммировать все вероятности состояний, то есть вычислить каждую (нормализованную) вероятность состояния. Число состояний увеличивается быстро с увеличением числа клиентов и/или узлов. В общем случае, можно рассматривать только маленькие системы. Сложность этой задачи подобна сложности задачи многоразмерных систем с потерями (Лекция 10).
неизвестно. Можно получить относительную нормализованную вероятность состояния. Наконец, нормализуя, мы получим нормализованные вероятности состояния. К сожалению, нормализация подразумевает, что необходимо суммировать все вероятности состояний, то есть вычислить каждую (нормализованную) вероятность состояния. Число состояний увеличивается быстро с увеличением числа клиентов и/или узлов. В общем случае, можно рассматривать только маленькие системы. Сложность этой задачи подобна сложности задачи многоразмерных систем с потерями (Лекция 10).
Мы покажем, как алгоритм свертывания может быть применен к сетям очередей. Алгоритм соответствует алгоритму свертывания для систем с потерями (Лекция 10). Рассмотрим сеть очередей с  узлами и единственной цепочкой очередей с
узлами и единственной цепочкой очередей с  клиентами. Принимаем условие, что системы организации очереди на каждом узле симметричны (секция 14.2). Алгоритм имеет три шага.
клиентами. Принимаем условие, что системы организации очереди на каждом узле симметричны (секция 14.2). Алгоритм имеет три шага.
-
Шаг 1. Пусть интенсивность прибытия заявок на произвольно выбранный
 -тый узел равна некоторому значению
-тый узел равна некоторому значению 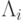 . Решая уравнения равновесия потока (14.5) для закрытой сети, получаем относительную интенсивность поступления
. Решая уравнения равновесия потока (14.5) для закрытой сети, получаем относительную интенсивность поступления 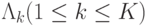 для всех узлов. В результате мы имеем значение относительной предложенной нагрузки
для всех узлов. В результате мы имеем значение относительной предложенной нагрузки  . Часто мы выбираем вышеупомянутую интенсивность прибытия заявок на узел так, чтобы предложенная нагрузка к этому узлу была равна единице.
. Часто мы выбираем вышеупомянутую интенсивность прибытия заявок на узел так, чтобы предложенная нагрузка к этому узлу была равна единице. -
Шаг 2. Рассмотрим каждый узел, как будто он изолированный и имеет предложенную нагрузку
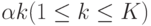 . В зависимости от фактической симметричной системы организации очереди на узле
. В зависимости от фактической симметричной системы организации очереди на узле  , получаем вероятность относительного состояния
, получаем вероятность относительного состояния 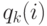 на узле
на узле  . Пространство состояний будет ограничено общим количеством клиентов
. Пространство состояний будет ограничено общим количеством клиентов  , то есть
, то есть  .
. - Шаг 3. Рекурсивно свернем вероятности состояния для каждого узла. Например, для первых двух узлов мы имеем:
 |
( 14.9) |
где:
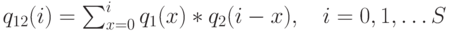
Когда для всех узлов получены свертки, получаем:
 |
( 14.10) |
Так как общее количество клиентов задано (  ), существует только состояние одной объединенной системы -
), существует только состояние одной объединенной системы -  и поэтому это макросостояние должно иметь вероятность появления, равную единице. Мы может тогда нормализовать все микровероятности состояний.
и поэтому это макросостояние должно иметь вероятность появления, равную единице. Мы может тогда нормализовать все микровероятности состояний.
Когда выполняется последнее свертывание, можно получить критерии качества работы для последнего узла. Изменяя порядок свертывания узлов, получим критерии качества работы всех узлов.
Пример 14.4.1: модель восстановления машин Пальма
Мы рассматриваем модель восстановления машин Пальма, введенную в секции 12.5, как закрытую сеть организации очередей (рис.14.5). Есть  клиентов и терминалов. Среднее время раздумья равно
клиентов и терминалов. Среднее время раздумья равно 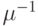 , и среднее время обслуживания центральным процессором -
, и среднее время обслуживания центральным процессором -  . В терминологии сети очередей есть два узла: первый узел является терминалом, то есть
. В терминологии сети очередей есть два узла: первый узел является терминалом, то есть 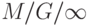 (фактически, это
(фактически, это  - система, но так как число клиентов ограничено S, которое может быть достаточно большим, это соответствует системе M/G/oo), и второй узел - центральный процессор, то есть
- система, но так как число клиентов ограничено S, которое может быть достаточно большим, это соответствует системе M/G/oo), и второй узел - центральный процессор, то есть 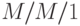 - система с сервисной интенсивностью
- система с сервисной интенсивностью 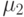 .
.
Потоки к узлам равны (  ), относительная нагрузка в узле 1 узле 2
), относительная нагрузка в узле 1 узле 2
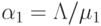
и
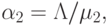
соответственно.
Если рассматривать каждый узел как изолированный, мы получаем вероятности состояния каждого узла,  и
и  . Свертывая
. Свертывая  и
и 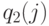 , получаем
, получаем  ,
,  , как показано в Таблице 14.1.
, как показано в Таблице 14.1.
Последний элемент с  клиентами (не нормализованная вероятность)
клиентами (не нормализованная вероятность)  состоит из:
состоит из:
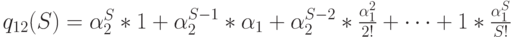
Где:
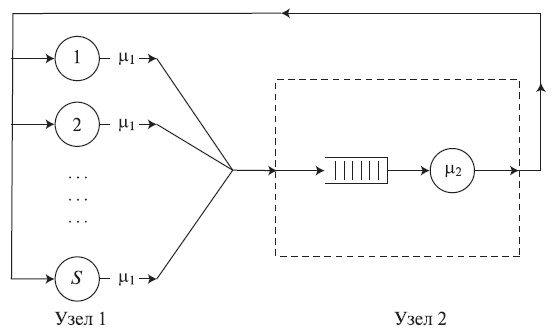
Рис. 14.5. Модель восстановления машин сети очередей с двумя узлами. Терминалы соответствуют одному узлу, где задачи всегда находят свободный терминал, в то время как центральный процессор, обрабатывающий заявки терминала - M/M/1-узел
Состояние  |
Узел 1 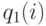 |
Узел 2  |
Сеть очередей  |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 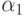 |
 |
 |
| 2 |  |
 |
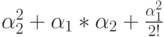 |
 |
 |
 |
 |
 |
 |
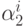 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Вероятность, что все терминалы находятся в режиме " раздумья ", отображается последним элементом (нормализованной суммы) (S терминалы в узле 1, нулевые терминалы в узле 2):

Это B- формула Эрланга. Таким образом, результат соответствует результату, полученному в секции 12.5. Заметим, что  появляется в той же самой степени во всех элементах
появляется в той же самой степени во всех элементах  и поэтому сокращается, когда мы нормализуем вероятности состояний.
и поэтому сокращается, когда мы нормализуем вероятности состояний.
Пример: Система с центральным сервером (обслуживающим прибором)
В 1971 г. Бузен (J. P. Buzen) ввел модель с центральным сервером (рис.14.6), чтобы рассмотреть мультипрограммную компьютерную систему с одним центральным процессором и множеством каналов ввода-вывода (периферийные модули). Степень мультипрограммирования  описывает число процессов, которые обрабатываются одновременно.
описывает число процессов, которые обрабатываются одновременно.
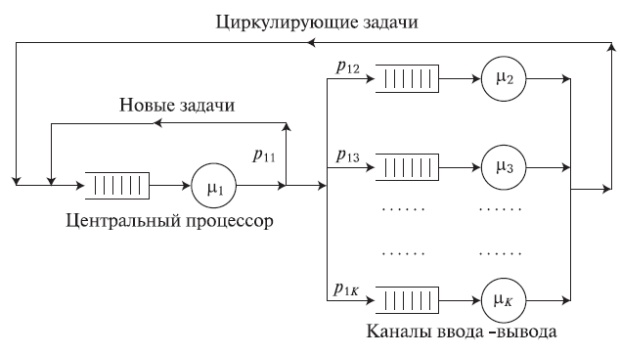
Рис. 14.6. Система организации очереди с центральным сервером, состоящая из одного центрального сервера и (K-1) каналов ввода-вывода. В системе циркулирует фиксированное число задач - S.
Число периферийных модулей обозначено  , как это можно видеть на рис.14.6, который также показывает вероятности переходов. Типично одна задача требует примерно сотню занятий либо центрального модуля, либо одного из внешних устройств. Мы принимаем что, как только задача закончена, она немедленно заменяется другой задачей, следовательно,
, как это можно видеть на рис.14.6, который также показывает вероятности переходов. Типично одна задача требует примерно сотню занятий либо центрального модуля, либо одного из внешних устройств. Мы принимаем что, как только задача закончена, она немедленно заменяется другой задачей, следовательно,  является постоянным. Все времена обслуживания - экспоненциально распределенные с интенсивностью
является постоянным. Все времена обслуживания - экспоненциально распределенные с интенсивностью 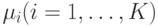 .
.
Бузен (Buzen) составил схему оценки этой системы. Схема - специальный случай алгоритма свертывания. Проиллюстрируем это для случая  клиента,
клиента,  узла и:
узла и:
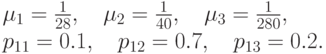
Относительные нагрузки равны:
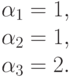
Если мы применяем алгоритм свертывания, то получаем результаты, показанные в Таблице 14.2. Элемент  состоит из:
состоит из:
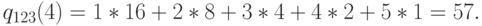
Узел 3 обслуживает клиентов во всех состояниях, кроме состояния  . Поэтому степень использования узла 3 равна
. Поэтому степень использования узла 3 равна  . На основании относительных нагрузок получаем точные нагрузки:
. На основании относительных нагрузок получаем точные нагрузки:
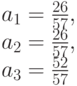
Среднее число клиентов в узле 3:
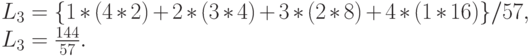
Изменяя порядок свертывания, получаем средние длины очереди 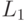 и
и 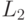 и в конце
и в конце 
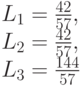
| Сост. | Узел 1 | Узел 2 | Узел 1*2 | Узел 3 | Сеть очередей |
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
| 0 | 1 | 1 | 2 | 2 | 4 |
| 1 | 1 | 1 | 3 | 4 | 11 |
| 2 | 1 | 1 | 3 | 4 | 11 |
| 3 | 1 | 1 | 4 | 8 | 26 |
| 4 | 1 | 1 | 5 | 16 | 57 |
Сумма всех средних длин очереди, конечно, равна числу клиентов  . Заметим, что в сетях организации очереди мы определяем длину очереди как общее количество клиентов в узле, включая обслуживаемых клиентов. Зная степень использования и среднее время обслуживания, находим среднее число клиентов, обслуженных в единицу времени на каждом узле:
. Заметим, что в сетях организации очереди мы определяем длину очереди как общее количество клиентов в узле, включая обслуживаемых клиентов. Зная степень использования и среднее время обслуживания, находим среднее число клиентов, обслуженных в единицу времени на каждом узле:
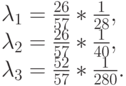
Применяя формулу Литтла, получаем среднее время пребывания