|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Распределение моментов поступления вызовов
Экспоненциальное распределение
В теории телетрафика это распределение также называется отрицательным экспоненциальным распределением. Оно было уже упомянуто в секции 3.1.2, и снова будет применяться в секции 6.2.1. В принципе, мы можем использовать любую функцию распределения с неотрицательными значениями, чтобы моделировать время "жизни". Однако экспоненциальное распределение имеет некоторые уникальные характеристики, которые имеют аналитическое и практическое использование. Экспоненциальное распределение играет ключевую роль среди всех распределений времени "жизни".
Это распределение характеризуется единственным параметром - интенсивностью или скоростью  :
:
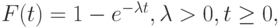 |
( 4.1) |
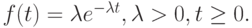 |
( 4.2) |
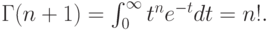 |
( 4.3) |
Мы заменяемый 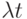 и получаем
и получаем  -тый момент
-тый момент
 |
( 4.4) |
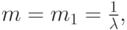
Второй момент:
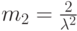

Коэффициент формы:
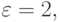
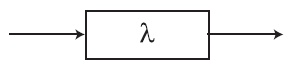
Рис. 4.1. В диаграммах состояния экспоненциально распределенный временной интервал изображают как блок с определенной интенсивностью. Блок означает, что клиент, прибывающий в него, задерживается перед тем, как покинуть блок, на экспоненциально распределенный временной интервал.
Экспоненциальное распределение очень подходит для описания физических временных интервалов (рис.4.2).
Самая фундаментальная характеристика экспоненциального распределения - отсутствие памяти.
Распределение остатка времени соединения связи не зависит от фактической продолжительности этого соединения, и равно распределению всего времени "жизни" (3.11):
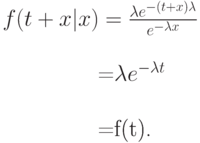
Если мы удаляем множество вероятностей в интервале (0, х) из функции плотности, и нормализуем остававшееся множество в интервале (х ,1) к единице, тогда новая функция плотности становится конгруэнтной (сравнимой) с первоначальной функцией плотности. Единственная непрерывная функция распределения, имеющая это свойство - экспоненциальное распределение, а дискретное распределение, обладающее этим свойством - геометрическое распределение.
Например, на рис.3.1 показано распределение Вейбулла, где это свойство не справедливо. Для k = 1 распределение Вейбулла становится идентичным экспоненциальному распределению. Поэтому средняя величина остаточного времени "жизни" - 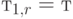 , и вероятность существования "жизни" в интервале (t, t+dt) , при условии, что она возникает после момента t, будет:
, и вероятность существования "жизни" в интервале (t, t+dt) , при условии, что она возникает после момента t, будет:
 |
( 4.5) |
Таким образом, вероятность существования "жизни" в интервале времени (t, t+ dt) зависит только от  и
и 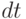 , но не зависит от фактического возраста (t).
, но не зависит от фактического возраста (t).
Минимум к экспоненциально распределенных случайных переменных
Пусть две случайных переменные  и
и  являются взаимно независимыми и экспоненциально распределенными с интенсивностями
являются взаимно независимыми и экспоненциально распределенными с интенсивностями 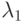 и
и 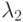 , соответственно. Новая случайная переменная
, соответственно. Новая случайная переменная  определяется как:
определяется как:
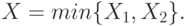
Функция распределения X равна:
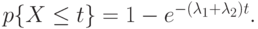 |
( 4.6) |
Эта функция распределения - тоже экспоненциальное распределение с интенсивностью 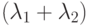 .
.
Согласно предположению, что первое (наименьшее) событие происходит в пределах временного интервала t, t+dt, вероятность, что случайная переменная  будет реализована первой (то есть, в этом интервале появится первой, а другая возникнет позже), будет равна:
будет реализована первой (то есть, в этом интервале появится первой, а другая возникнет позже), будет равна:
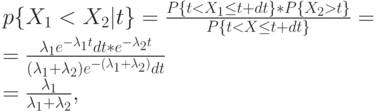 |
( 4.7) |
то есть, независимо от t. Таким образом, мы не должны интегрировать по всем значениям t.
Эти результаты могут быть обобщены на k переменных, и приниматься как основной принцип методики моделирования, называемый метод рулетки или метод моделирования Монте-Карло.
Комбинация экспоненциальных распределений
Если с помощью одного экспоненциального распределения (то есть одного параметра) мы не можем описать достаточно детально временные интервалы, то нам, вероятно, придется использовать комбинацию двух или больше экспоненциальных распределений. Пальма ввел два класса распределений: крутое и плоское. Крутое распределение соответствует набору последовательных, стохастических независимых экспоненциальных распределений (рис.4.2), а плоское соответствует параллельным экспоненциальным распределениям (рис.4.4). Такая структура естественно позволяет описать процессы нагрузки в телекоммуникации и сетях передачи данных.
Комбинируя крутое и плоское распределения, мы можем получить произвольно хорошее приближение для любой функции распределения (см. рис.4.7 и секцию 4.4). Диаграммы на рис.4.2 и рис.4.4 называются фазовыми диаграммами (или диаграммами состояний).
Комбинируя k экспоненциальных распределений последовательно, получаем крутое распределение  . Если все k распределения идентичны (
. Если все k распределения идентичны (  ), то мы получаем k распределение Эрланга
), то мы получаем k распределение Эрланга

