Восходящие анализаторы

Алгоритм построения конечного автомата

Теперь обсудим алгоритм построения анализатора. Во-первых, пополним грамматику. Обозначим T множество состояний, E - множество переходов.

T = {closure ([S'->.S])};
E = {};
do 
{
   for (каждого состояния I из T)
   {
      for (каждой ситуации [A->w.Xv] из  I)
      {
         J = goto (I, X);
         T+={J};      /* ко множеству состояний добавляется новое состояние */
         E+=(I->J);   /* ко множеству ребер добавляется ребро, идущее из  
                         состояния I в состояние J. Этот переход 
                         осуществляется по символу X */
      }
   }
} while (E или T изменились);

Поскольку для символа $ операция goto (I, $) не определена, мы выполняем действие accept .

Автомат для грамматики

Для определенной нами грамматики автомат получится следующим:

где состояния определяются следующим образом:

0: {[S'.S], [S->.x], [S->.(L)]}
1: {[S->x.]}
2: {[S-> (.L)], [L->.L,S], [L->.S], [S->.(L)], [S->.x]}
3: {[S'->S.]
4: {[S-> (L.)], [L->L., S]}
5: {[S-> (L).]}
6: {[L->S.]}
7: {[L->L,.S], [S->.(L)], [S->.x]}
8: {[L->L,S.]}

Управляющая таблица

Теперь мы можем вычислить множество сверток R :

R = empty set;
for (each state I in T)
{
   for (each item [A->w.] in I)
   {
      R+={(I, A->w)};
   }
}

Таким образом, алгоритм построения управляющей таблицы автомата состоит из следующих шагов:

• Пополнение грамматики
• Построение множества состояний
• Построение множества переходов
• Построение множества сверток

Для того, чтобы построить таблицу анализатора для грамматики, поступим следующим образом:

1. для каждого ребра I->X J мы поместим в позицию [I, X] таблицы
   • shift J , если X - терминал,
   • goto J , если X - нетерминал.
2. для каждого состояния I , содержащего ситуацию [S'->S.] мы поместим accept в позицию [I,$]
3. для состояния, содержащего ситуацию [A->w.] (правило номер n с точкой в конце правила), поместим reduce n в позицию [I, Y] для каждого терминала Y .
4. пустая ячейка означает ошибочную ситуацию

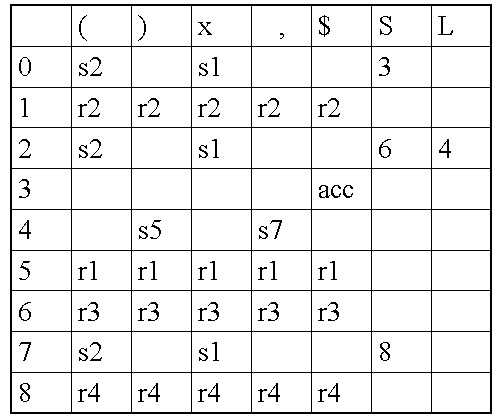
Приведем управляющую таблицу для грамматики G₀: