| Россия |
Инспектор
Спонсор: Microsoft
Вы можете этот курс.
Опубликован: 23.07.2006 | Уровень: специалист | Доступ: платный
Лекция 6:
Синтаксические анализаторы. Нисходящие анализаторы
Условия использования метода рекурсивного спуска
Метод рекурсивного спуска без возвратов можно использовать только для грамматик, правила которых удовлетворяют следующему условию: первого символа каждого правила должно быть достаточно для того, чтобы определить, какое правило применимо в данном случае. Более точно это условие можно формализовать путем определения множества FIRST.
Определение.Для КС-грамматики G и цепочки w, состоящей из терминальных и нетерминальных символов, определим множество FIRST k (w) следующим образом:
FIRST k (w) = {x | w =>* xv, |x| = k или w =>* x, |x| < k}, где k - натуральное число.Иными словами, множество FIRST k (w) состоит из всех терминальных префиксов длины k терминальных цепочек, выводимых из w.
Пример.Рассмотрим грамматику, порождающую подмножество типов языка Pascal.
![type \to imple
\\
type \to \widehat{\ }\,\textbf{id}
\\
type \to \textbf{array}\ [simple]\ \textbf{of}\ type
\\
simple \to \textbf{integer}
\\
simple \to \textbf{char}
\\
simple \to \textbf{num .. num}](/sites/default/files/tex_cache/5cd0dc5d764bbf3c761abec9f133d0f4.png)
Для этой грамматики мы имеем:
FIRST1 (simple) = {integer, char, num}
FIRST1 (^id) = {^}
FIRST1 (array [simple] of type) = { array }Понятно, что если цепочка w состоит только из терминалов, то FIRST k (w) - это первые k символов цепочки w , если |w| >=, или это сама цепочка w, если |w| < k <
Алгоритм построения множества FIRST
Прежде всего, определим множество FIRST для всех символов грамматики:
- если X - терминал, то FIRST (X) = X
- для правила
добавим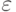 
к множеству FIRST (X)
- если X - нетерминал и
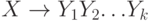- правило грамматики, то добавим терминал а в FIRST(X), если для некоторого i этот терминал a принадлежит 
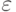и принадлежит всем
множествам 
, 
, то есть 
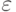Если принадлежит 
для всех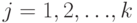 
, то добавим 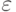в FIRST(Y).
Теперь сформулируем сам алгоритм построения множества FIRST(w).
Вход.КС-грамматика G=(N, T, P, S) и цепочка w терминальных и нетерминальных символов.
Выход. FIRST (w).
Метод.Добавим в FIRST (X 1 X 2 …X k) все непустые символы из FIRST (X1). Затем, если 
принадлежит FIRST (X1), то добавим все непустые символы из FIRST (X2), и так далее. Наконец, если для всех j FIRST (Xj) содержит пустой символ, то мы добавим в множество FIRST (X1 X2…Xk) .
Пример.Рассмотрим грамматику с правилами:
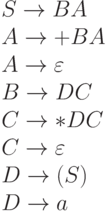
Для этой грамматики множества FIRST определяются следующим образом:
