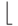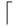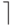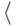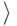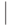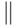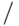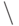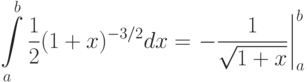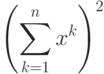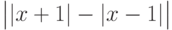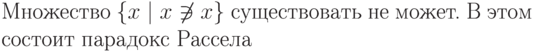Как набирать формулы
Скобки переменного размера
Если заключенный в скобки фрагмент формулы занимает много места по вертикали (за счет дробей, степеней и тому подобного), то и сами скобки должны быть большего размера, чем обычные. В TeX'е на этот случай предусмотрен механизм автоматического выбора размера скобок. Пользуются им так.
В формуле
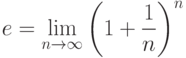
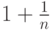 смотрелись бы плохо;
поэтому при ее наборе надо поставить команду \left перед
открывающей скобкой и команду \right перед закрывающей:
смотрелись бы плохо;
поэтому при ее наборе надо поставить команду \left перед
открывающей скобкой и команду \right перед закрывающей:$$
e=\lim_{n\to\infty}
\left(1+\frac{1}{n}\right)^n
$$Если перед одной скобкой стоит \left, а перед другой скобкой стоит \right, то на печати размер этих скобок будет соответствовать максимальной высоте фрагмента формулы, заключенного между \left и \right.
Конструкция с \left и \right применима не только к круглым скобкам. В следующей таблице перечислены скобки и некоторые другие символы, которые с помощью \left и \right автоматически принимают нужный размер. TeXнический термин для таких символов — ограничители (по-английски delimiters).
Вместо \left\langle можно писать \left<, и аналогичным образом вместо \right\rangle можно писать \right> (однако же < нельзя писать вместо \langle!). Кроме знаков, перечисленных в этой таблице, менять свои размеры под действием \left и \right могут и вертикальные стрелки из таблицы.
Если подключить стилевой пакет amssymb, то станут доступны еще две пары ограничителей:
Вместе с каждой командой \left в формуле должна присутствовать соответствующая ей команда \right, в противном случае TeX выдаст сообщение об ошибке. Вместе с тем TeX вовсе не требует, чтобы "ограничители" (например, скобки) при командах \left и \right были расположены сколько-нибудь осмысленно с математической точки зрения: вы вполне можете написать что-нибудь вроде \left(...\right], или даже, вопреки смыслу слов left и right, \left)...\right( - за правильность своих формул отвечаете только вы, и TeX тут вам не помощник.
Вместо "ограничителя" после команды \left или \right можно поставить точку. На месте этой точки ничего не напечатается, а другой "ограничитель" будет необходимого размера. Вот два примера того, как можно использовать этот прием. Во-первых, таким способом можно создать косую дробную черту увеличенного размера (символ {/} также является "ограничителем"- см. ниже):
В этом примере используется пока неизвестная вам команда \,
создающая дополнительный маленький пробел между  и
и  - это
один из немногих случаев, когда TeX не может автоматически создать
требуемые пробелы, и ему надо помочь. Подробнее о таких вещах речь
пойдет ниже, в разд. "Пробелы вручную". Другой пример использования
ограничителя без пары таков:
- это
один из немногих случаев, когда TeX не может автоматически создать
требуемые пробелы, и ему надо помочь. Подробнее о таких вещах речь
пойдет ниже, в разд. "Пробелы вручную". Другой пример использования
ограничителя без пары таков:
Здесь, кстати, мы не поставили \ перед x, поскольку необходимое свободное место возникает за счет показателя степени.
Наконец, важный пример использования ограничителей без пары — использование их для набора систем уравнений, о чем пойдет речь в разд."Многострочные включные формулы".
До сих пор у нас речь шла только о том, что размеры ограничителей выбираются автоматически с помощью команд \left и \right ; бывают, однако, ситуации, когда такой автоматический выбор размера приводит к неудовлетворительным результатам или даже вообще невозможен. Вот, например, ситуация, когда \left и \right не срабатывают:
Для удобочитаемости этого выражения хотелось бы, чтобы внешние знаки модуля были повыше, чем внутренние, но этого не получается: поскольку в формуле выступающих элементов нет, то и команды \left и \right не считают нужным увеличить ограничители, в которые формула заключена.
А иногда бывает так, что автоматически получающиеся ограничители слишком велики. В следующем примере совсем не обязательно, чтобы скобки охватывали и пределы суммирования, что получается при использовании \left и \right:
Во всех этих случаях имеет смысл указать размер ограничителя явно. Для этого предусмотрены TeX'овские команды \bigl, \Bigl, \biggl и \Biggl для левых ограничителей и \bigr, \Bigr, \biggr и \Biggr для правых ограничителей. Мы перечислили эти команды в порядке возрастания размера создаваемого ими ограничителя. В частности, для модулей можно было бы написать так:
Пример со знаком суммы кому-то мог бы понравиться больше, если бы мы написали так:
Команды, явно указывающие размер ограничителей, не обязаны, в отличие от команд \left и \right, появляться парами: можно написать \biggl ( и при этом никак не упомянуть о парной скобке.
К сожалению, команды для явного указания размера ограничителя имеют одну неприятную особенность: если " основной шрифт" документа крупнее, чем кегль 10 (иными словами, если указаны классовые опции 11pt или 12pt — , то может случиться так, что скобка, размер которой задан, например, командой \bigl, имеет точно такой же размер, как и скобка "в чистом виде". Чтобы избежать этой неприятности, надо подключить пакет amsmath: тогда команды наподобие \bigl будут работать корректно.
Перечеркнутые символы
Чтобы получить в математической формуле изображение перечеркнутого символа, надо перед командой, генерирующей этот символ, поставить команду \not. Пример:
Кстати, для получения знака 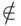 лучше не
писать "\not\in", а воспользоваться командой \notin —
при этом знак получится более красивым. Если подключен
пакет amssymb, то можно также вместо команды \not
пользоваться готовыми командами для перечеркнутых
символов .
лучше не
писать "\not\in", а воспользоваться командой \notin —
при этом знак получится более красивым. Если подключен
пакет amssymb, то можно также вместо команды \not
пользоваться готовыми командами для перечеркнутых
символов .

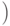
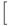
![]](/sites/default/files/tex_cache/0fbd1776e1ad22c59a7080d35c7fd4db.png)