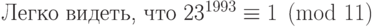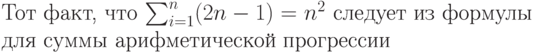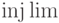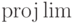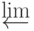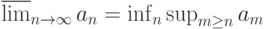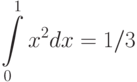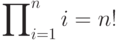Как набирать формулы
Операции с пределами и без
В следующей таблице собраны названия функций — команды
для воспроизведения названий математических операций
наподобие  ,
, 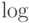 и т.п., обозначаемых последовательностью букв, набираемых
прямым шрифтом. Любую из этих операций можно снабдить верхним и/или
нижним индексом .
и т.п., обозначаемых последовательностью букв, набираемых
прямым шрифтом. Любую из этих операций можно снабдить верхним и/или
нижним индексом .
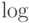 |
\log |
 |
\lg |
 |
\ln |
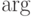 |
\arg |
 |
\ker |
 |
\dim |
 |
\hom |
 |
\deg |
 |
\exp |
 |
\sin |
 |
\arcsin |
 |
\cos |
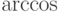 |
\arccos |
 |
\tan |
 |
\arctan |
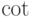 |
\cot |
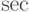 |
\sec |
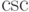 |
\csc |
 |
\sinh |
 |
\cosh |
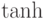 |
\tanh |
 |
\coth |
В этой таблице обозначения  ,
,  и т.д. — не что иное, как принятые в англоязычной
литературе обозначения для тангенса, арктангенса и т.д.
В отечественной литературе, однако же, принято обозначать
и т.д. — не что иное, как принятые в англоязычной
литературе обозначения для тангенса, арктангенса и т.д.
В отечественной литературе, однако же, принято обозначать 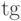 ,
, 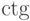 и т.д. Так как в стандартном комплекте
TeX'а или LaTeX'а команд для этого нет, их приходится, при
необходимости, определять самому. Это просто: надо подключить
пакет amsmath, после чего добавить в преамбулу такую
строчку:
и т.д. Так как в стандартном комплекте
TeX'а или LaTeX'а команд для этого нет, их приходится, при
необходимости, определять самому. Это просто: надо подключить
пакет amsmath, после чего добавить в преамбулу такую
строчку:
\DeclareMathOperator{\tg}{tg}В первом аргументе команды \DeclareMathOperator ставится придуманное вами имя команды (незанятое, естественно), во втором — то, что вы хотите получить на печати. Содержимое второго аргумента будет обработано, как математическая формула, но при этом символы - (дефис), * и ' будут иметь такое же значение, как в обычном тексте (это удобно, если вы хотите, чтобы имя вашего нового оператора включало тот же дефис). Разумеется, \DeclareMathOperator должно следовать в преамбуле документа после \usepackage{amsmath}.
Если не подключать amsmath, то собственную функцию,
например tangens, определить также можно. Для этого достаточно
написать в преамбуле документа \newcommand{\tg}{\mathop{\mathrm{tg}}\nolimits}
После этого команда \tg будет создавать в математической
формуле запись 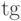 с правильными пробелами вокруг нее. Другие
команды такого типа определяются аналогично, надо только
вместо tg написать то название функции
(скажем, arctg ), которое должно появиться на печати.
с правильными пробелами вокруг нее. Другие
команды такого типа определяются аналогично, надо только
вместо tg написать то название функции
(скажем, arctg ), которое должно появиться на печати.
В частности, так приходится делать, чтобы определить
команды \Re
и \Im для обозначения
вещественной и мнимой части комплексного числа; в LaTeX'е такие
команды есть, но на печати они дают не  и
и  , а
, а  и
и 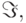 что не
принято в России (да и на Западе не очень принято). При этом,
поскольку обозначения \Re и \Im уже заняты, приходится
говорить \renewcommand вместо \newcommand:
что не
принято в России (да и на Западе не очень принято). При этом,
поскольку обозначения \Re и \Im уже заняты, приходится
говорить \renewcommand вместо \newcommand:
\renewcommand{\Im}{\mathop{\mathrm{Im}}\nolimits}Даже при подключенном пакете \amsmath команда \DeclareMathOperator в этом месте не сработает, т.к. уже существующие команды она не переопределяет.
Описанный выше способ определения команд для функций является частным случаем существующей в LaTeX'е конструкции для (пере)определения новых команд (см. "Создание новых команд" ).
Еще один символ, который принято набирать прямым шрифтом, — это
символ  , используемый в записи "сравнений по
модулю". Обычно он употребляется не сам
по себе, а в сочетании со знаком
, используемый в записи "сравнений по
модулю". Обычно он употребляется не сам
по себе, а в сочетании со знаком 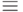 (см. пример ниже); в этом
случае для записи сравнения удобна команда \pmod, которой
пользуются так:
(см. пример ниже); в этом
случае для записи сравнения удобна команда \pmod, которой
пользуются так:
Обратите внимание, что скобки вокруг  получаются
автоматически; правая часть сравнения — весь текст, заключенный
между \equiv и \pmod.
получаются
автоматически; правая часть сравнения — весь текст, заключенный
между \equiv и \pmod.
Если подключить пакет amsmath, то станут доступны команды \mod и \pod, обозначающие то же понятие, что \mod, другими способами:
Иногда символ  используется и как символ бинарной операции, например, так:
используется и как символ бинарной операции, например, так:
Как видно из примера, в этом случае надо писать \bmod.
Теперь обсудим, как можно было бы получить, скажем, формулу
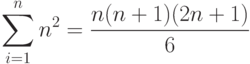
c дополнительными элементами над и под знаком операции. В данной формуле эти элементы называются "пределы суммирования", поэтому в TeX-нической терминологии записи над и под знаком операции принято называть "пределами" (по-английски limits). В исходном тексте "пределы" обозначаются точно так же, как индексы; имея в виду, что знак суммы генерируется командой \sum, заключаем, что вышеназванную формулу можно получить так: \sum_{i=1}^n n^2=\frac{n(n+1)(2n+1)}{6}
В этом примере существенно, что формула была выключной; во внутритекстовой формуле "пределы" печатаются на тех же местах, что и индексы:
(можно добиться, чтобы пределы и во внутритекстовой формуле были сверху и снизу — см. ниже). Вот список операций, ведущих себя так же, как \sum:
 |
\sum |
 |
\prod |
 |
\bigcup |
 |
\bigcap |
 |
\coprod |
 |
\bigoplus |
 |
\bigotimes |
 |
\bigodot |
 |
\bigvee |
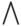 |
\bigwedge |
 |
\biguplus |
 |
\bigsqcup |
 |
\lim |
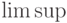 |
\limsup |
 |
\liminf |
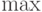 |
\max |
 |
\min |
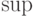 |
\sup |
 |
\inf |
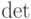 |
\det |
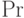 |
\Pr |
 |
\gcd |
Если подключить пакет amsmath, то будут доступны еще шесть операций такого типа:
Примеры:
|
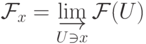 |
$\varlimsup_{n\to\infty}
a_n=\inf_n\sup_{m\ge n}a_m$$\mathcal F_x=
\varinjlim_{U\ni x}
\mathcal F(U)$ |
(см. далее по поводу \mathcal ).
Кроме того, пакет amsmath предоставляет возможность
определить и собственную команду "с пределами". Для
этого надо воспользоваться
командой \DeclareMathOperator* ;
синтаксис этой команды такой же, как у
команды \DeclareMathOperator, но
при "операторе", определенном такой командой, "
пределы" будут ставиться так же, как при  .
.
Еще одна "математическая операция", для которой требуются "
пределы", — это интеграл. В LaTeX'е есть
команды \int для обычного знака
интеграла 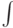 и \oint для знака "контурного
интеграла"
и \oint для знака "контурного
интеграла"  ; если подключить пакет amsmath, то
станут доступны также команды \iint, \iiint и \iiiint для двойного,
тройного и "
четверного" интегралов (если просто написать несколько
команд \int подряд, то между знаками
интеграла получатся слишком большие пробелы).
; если подключить пакет amsmath, то
станут доступны также команды \iint, \iiint и \iiiint для двойного,
тройного и "
четверного" интегралов (если просто написать несколько
команд \int подряд, то между знаками
интеграла получатся слишком большие пробелы).
При этом, для экономии места, пределы интегрирования помещаются не сверху и снизу от знаков интеграла, а по бокам (даже и в выключных формулах):
Если, тем не менее, необходимо, чтобы пределы интегрирования стояли над и под знаком интеграла, то надо непосредственно после \int записать команду \limits, а уже после нее — обозначения для пределов интегрирования:
Тот же прием с командой \limits можно применить, если хочется, чтобы во внутритекстовой формуле "пределы" у оператора стояли над и под ним, а не сбоку.
Если, с другой стороны, надо, чтобы в выключной формуле " пределы" у какого-либо оператора стояли не над и под знаком оператора, а сбоку, то после команды для знака оператора надо записать команду \nolimits, а уже после нее — обозначения для "пределов"