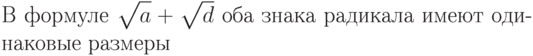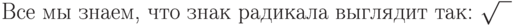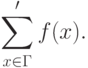Как набирать формулы
Фантомы и прочее
Ранее мы столкнулись с командой \lefteqn, позволяющей напечатать фрагмент формулы и при этом сообщить TeX'у, что отдельного места (по горизонтали) на этот фрагмент отводить не надо. Иногда бывает полезно сделать обратное: включить в формулу символ, который сам не печатается, но место занимает. Вот пример такой ситуации.
Команда \sqrt автоматически выбирает размер знака радикала таким образом, чтобы он точно соответствовал высоте подкоренного выражения, и это очень хорошо. Иногда, однако, такой автоматический выбор приводит к не очень удачным результатам:
Дело тут, конечно, в том, что буквы  и
и  имеют
разную
высоту. Чтобы сделать знаки радикала одинаковыми, TeX надо
обмануть: добавить в подкоренные выражения по символу, который
чуть выше, чем
имеют
разную
высоту. Чтобы сделать знаки радикала одинаковыми, TeX надо
обмануть: добавить в подкоренные выражения по символу, который
чуть выше, чем  или
или  , чтобы подкоренные выражения
оказались
одной высоты. Этот символ, естественно, не должен печататься и не
должен занимать места по горизонтали (лишние пробелы под корнем
нам тоже ни к чему). Такой невидимый символ генерируется TeX'овской
командой \mathstrut:
, чтобы подкоренные выражения
оказались
одной высоты. Этот символ, естественно, не должен печататься и не
должен занимать места по горизонтали (лишние пробелы под корнем
нам тоже ни к чему). Такой невидимый символ генерируется TeX'овской
командой \mathstrut:
Точнее говоря, \mathstrut - это невидимый символ, равный по
высоте скобке 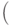 и не имеющий ширины.
и не имеющий ширины.
Невидимый символ, создаваемый командой \mathstrut, является частным случаем TeX'овской конструкции "фантома". Именно, если в формуле вы напишете
"\phantom{"TeXtit{какая-то формула} "}"то результат будет такой же, как если бы эта самая "какая-то формула" была сначала напечатана по всем правилам TeX'а, а затем аккуратно стерта с бумаги. Пример:
Кроме того, можно создать "вертикальный фантом" формулы (по вертикали будет оставлено столько же места, сколько занимала бы формула, по горизонтали вертикальный фантом места не занимает). Создается вертикальный фантом командой \vphantom. В частности, команда \mathstrut - это сокращение для "\vphantom{(}" . Возможны, наконец, и горизонтальные фантомы, занимающие по горизонтали столько же места, сколько заняла бы формула, и не занимающие места по вертикали. Создаются они командой \hphantom:
Для полноты картины скажем об еще одной экзотической команде, называемой \smash. Подобно команде \lefteqn, она печатает символ, но при этом говорит TeX'у, что он не занимает места по вертикали. С помощью этой команды (а так же с помощью \lefteqn ) можно накладывать в формулах один символ на другой. Вот пример совместной работы команд \phantom и \lefteqn:
Поясним, как устроен исходный текст, давший такое перекрытие скобок.
Верхняя фигурная скобка, созданная командой \overbrace, ставится
не над самой формулой 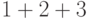 , а над ее фантомом. В результате
команда \overbrace печатает фигурную скобку над пустым местом.
Далее, вся эта конструкция стоит, в свою очередь, в аргументе
команды \lefteqn, вследствие чего TeX считает, что места по
горизонтали она не занимает. Поэтому
формула
, а над ее фантомом. В результате
команда \overbrace печатает фигурную скобку над пустым местом.
Далее, вся эта конструкция стоит, в свою очередь, в аргументе
команды \lefteqn, вследствие чего TeX считает, что места по
горизонтали она не занимает. Поэтому
формула  начинается с того же места, что и фантом формулы
начинается с того же места, что и фантом формулы 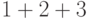 ; в
результате
; в
результате 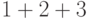 попадает аккурат под верхнюю скобку! Все это,
конечно, — еще один пример "грязного трюка").
попадает аккурат под верхнюю скобку! Все это,
конечно, — еще один пример "грязного трюка").
Если бы формула была не выключная, а внутритекстовая, то этот трюк прошел бы не столь гладко. Дело в том, что команда \lefteqn всегда набирает формулы в \displaystyle, поэтому размер фантома, над которым ставилась скобка, мог в принципе не совпасть с размером реально печатаемого фрагмента формулы. Чтобы уж совсем себя обезопасить, следовало бы в этом случае аргумент команды \lefteqn начать с \textstyle.
Снова об интервалах в формулах
Сейчас мы обсудим вкратце, какими правилами руководствуется TeX при расстановке интервалов в математических формулах. В стандартных ситуациях мы об этом не задумываемся, а полностью доверяем LaTeX'у. То, о чем мы будем говорить, пригодится, если мы пользуемся в формулах сложными конструкциями (например, конструируем знак двойного интеграла из двух знаков интеграла и "отрицательных пробелов", и при этом не хотим подбирать верные интервалы экспериментально.
При наборе формулы TeX рассматривает ее как состоящую из частей одного из следующих типов:
| Обыкновенный символ | например, \alpha |
| Бинарная операция | |
| Бинарное отношение | |
| Математический оператор | |
| Подформула | например, {x^2} |
| Знак препинания | , или ; или \colon или \ldotp |
| Скобка |
Здесь подформула — это любой фрагмент формулы, заключенный в фигурные скобки. Команда \colon задает двоеточие, рассматриваемое как знак препинания (двоеточие, набранное непосредственно, рассматривается TeX'ом как знак бинарного отношения), а команда \ldotp — точку, рассматриваемую как знак препинания (точка, набранная непосредственно, рассматривается как обыкновенный символ). К бинарным отношениям (с точки зрения TeX'а) относятся также все стрелки (\стр{arrows}) и фрагменты формул, создаваемые командой \stackrel. При расстановке пробелов в формуле TeX руководствуется тем, к какому из перечисленных типов относятся ее составные части: символы бинарных операций окружаются "средними пробелами" (теми, что вручную задаются командой \:), а символы бинарных отношений — "толстыми" пробелами (вручную, как мы помним, толстый пробел задается командой \; ); впрочем, в стилях для индексов и индексов к индексам (см. предыдущий раздел) эти пробелы опускаются; после знака препинания в большинстве случаев ставится "тонкий" пробел, и т.д2Иногда полезно поставить пустые фигурные скобки {\{\}}, чтобы создать фиктивный аргумент бинарной операции и тем самым обеспечить желательные пробелы; мы делали это в примере на с.38 Подформула (т. е. фрагмент формулы, заключенный в фигурные скобки) рассматривается TeX'ом почти так же, как обычный символ:
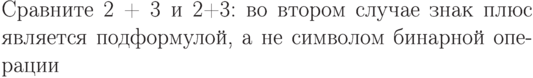 |
Сравните $2+3$ и $2{+}3$:
во втором случае знак
плюс является подформулой,
а не символом
бинарной операции. |
Кстати, с этим приемом (поставить фрагмент формулы в фигурные скобки, чтобы он рассматривался как обычный символ) мы уже сталкивались ранее, когда обсуждали, как задать в TeX'е десятичную дробь. Мы не будем вдаваться в точные правила расстановки пробелов (они перечислены в книге [2]). Для нас сейчас важнее то, что TeX можно заставить рассматривать любой фрагмент формулы как бинарную операцию, бинарное отношение или математическую операцию: для этого надо применить команды \mathbin, \mathrel или \mathop соответственно. Вот примеры того, как работают эти команды.
Иногда возникает нужда в символе  , рассматриваемом
как символ бинарной операции. Естественно, этот символ можно
сгенерировать, если написать \hat{\otimes}, но тогда
вокруг этого символа будут неправильные пробелы:
, рассматриваемом
как символ бинарной операции. Естественно, этот символ можно
сгенерировать, если написать \hat{\otimes}, но тогда
вокруг этого символа будут неправильные пробелы:
 |
Хотелось бы, чтобы в формуле
$E\hat{\otimes}F$ были такие
же пробелы, как и в
формуле $E\otimes F$. |
Чтобы TeX рассматривал  не как обычный символ,
а как символ бинарной операции, надо сделать так:
не как обычный символ,
а как символ бинарной операции, надо сделать так:
Если символ  встречается в вашей рукописи часто, то
вам
вряд ли понравится всякий раз делать по 23 нажатия на клавиши для его
набора. В этом случае очень удобно ввести для него собственное
сокращенное обозначение (посмотрите начало
"Создание новых команд"
по поводу
того, как это сделать).
встречается в вашей рукописи часто, то
вам
вряд ли понравится всякий раз делать по 23 нажатия на клавиши для его
набора. В этом случае очень удобно ввести для него собственное
сокращенное обозначение (посмотрите начало
"Создание новых команд"
по поводу
того, как это сделать).
Типичный пример использования команды \mathop - определение
имени операции, записываемой прямым шрифтом. Обозначения такого типа
встречаются в математических текстах очень часто, и набора команд для
них, предусмотренного LaTeX'ом , вполне может не
хватить; в этом случае, чтобы получить на печати, скажем, 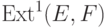 , надо написать
, надо написать
$\mathop{\mathrm{Ext}}\nolimits^1(E,F)$Здесь \mathop необходимо для того, чтобы
между  и
и 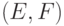 автоматически вставлялся
маленький дополнительный пробел, делающий формулу более читаемой:
автоматически вставлялся
маленький дополнительный пробел, делающий формулу более читаемой:
Что же касается \nolimits, то эта команда необходима для того, чтобы в выключных формулах (точнее, в "выключном стиле"- верхние и нижние индексы к " оператору" записывались именно как индексы, а не над и под ним, как "пределы" . Именно таким образом работает определенная в пакете amsmath команда \DeclareMathOperator.
А вот пример, когда TeX'у надо объяснить, что некоторый сложный символ есть символ математического оператора. Пусть нам понадобилась формула
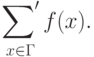
В самом деле, из сказанного на стр.54 вытекает, что наша запись равносильна такой:
$$
\sum^\prime_{x\in\Gamma}f(x).
$$и в этой записи штрих рассматривается как предел суммирования. Не будем, однако, отчаиваться, а просто создадим новый оператор "сумма со штрихом":
$$
\mathop{{\sum}'}_{x\in\Gamma}f(x).
$$Можете проверить, что на сей раз все получается как надо. В этой записи очень существенно, что \sum взято в фигурные скобки: благодаря этому символ, генерируемый командой \sum, рассматривается TeX'ом просто как подформула, поэтому и штрих после него стоит где положено, а не там, где бывают пределы суммирования. Вся подформула "{\sum}" передается в качестве аргумента команде \mathop, благодаря чему наш новый символ "сумма со штрихом" рассматривается как математический оператор и пределы суммирования (в выключной формуле) ставятся у него, где положено.
Здесь опять разумно создать сокращенное обозначение, которое заменяло бы эту громоздкую запись.
Вертикальные отбивки вокруг выключных формул
За размер вертикальных отбивок, автоматически создаваемых TeX'ом вокруг выключных формул, отвечают следующие TeX'овские параметры:
| \abovedisplayskip | \abovedisplayshortskip | перед формулой |
| \belowdisplayskip | \belowdisplayshortskip | после формулы |
В каждой из этих пар второй параметр относится к случаю, когда и формула, и соседняя с ней строка текста коротки (в таком случае расстояние между формулой и текстом должно быть поменьше). Если вы хотите уменьшить эти отбивки, скажем, на 30%, напишите в преамбуле
\abovedisplayskip=.7\abovedisplayskip
(и аналогично для трех остальных параметров).
Можно не только пропорционально изменять отбивки вокруг выключных формул, как в примере выше, но и присваивать этим интервалам конкретные значения. При этом следует иметь в виду следующее обстоятельство. Интервалы, создаваемые между текстом и формулами, обладают определенной растяжимостью, что помогает TeX'у выравнивать страницы по высоте (говоря на TeX'ническом языке, эти интервалы являются "клеем"), и присваивая абсолютное значение таким интервалам, желательно также задавать их растяжимость и сжимаемость; (более подробно — разд. "Клей" "Блоки и клей" по поводу того, как это делается.
Горизонтальные отбивки вокруг формул
Некоторые авторы и издатели считают, что математический текст выглядит понятнее, когда каждая формула окружена дополнительным пробелами справа и слева от нее {Это актуально для текстов на языках с латинской графикой. В русских текстах формулы обычно достаточно выделяются уже за счет того, что в них используется латиница, а в тексте — кириллица.}. Для этих целей в TeX'е предусмотрен параметр \mathsurround. Значение этого параметра — размер дополнительного пробела, вставляемого по обе стороны каждой внутритекстовой математической формулы (этот пробел не добавляется перед формулой, попавшей при печати в начало строки, и после формулы, попавшей в конец строки). При запуске LaTeX'а значение этого параметра равно нулю, так что расстояния между формулами и окружающим текстом такие же, как между словами в тексте. Можно, однако, присвоить параметру \mathsurround ненулевое значение. Например, команда \mathsurround=2pt (будучи включена в преамбулу) окружает каждую формулу дополнительными пробелами по 2 пункта с обеих сторон.
Если нужно организовать дополнительные горизонтальные отбивки вокруг какой-то одной формулы, можно поместить команду, присваивающую значение параметру \mathsurround, непосредственно в саму формулу (между ограничивающими ее знаками доллара, в любое место). Важно только не забыть сделать пробел после обозначения для единицы длины (скажем, pt).