| Россия |
Статический анализ деталей
Статический анализ позволяет осуществлять расчёт напряжённого состояния конструкций под действием приложенных к системе постоянных во времени сил. На сегодняшний день это, пожалуй, наиболее востребованная в проектировании задача. С помощью модуля "Статический анализ" пользователь может оценить прочность разработанной им конструкции по допускаемым напряжениям, определить наиболее слабые места конструкции и внести необходимые изменения (оптимизировать) изделие. При этом между трёхмерной моделью изделия и расчётной конечно-элементной моделью поддерживается ассоциативная связь.
1. Теоретическая часть
Статический анализ позволяет осуществлять расчёт напряжённо-деформированного состояния конструкций под действием приложенных к системе постоянных во времени сил. Также можно учесть напряжения, возникающие по причине температурного расширения/сжатия материала или деформации конструкции на величину известных перемещений.
Модуль "Статический анализ" позволяет оценить прочность разработанной конструкции по допускаемым напряжениям, определить наиболее уязвимые места конструкции, внести необходимые изменения и таким образом оптимизировать конструкцию детали или изделия.
Для построения дискретной математической модели, адекватно отражающей физическую сущность и свойства исследуемой конструкции, применяется метод конечных элементов. Важнейшим элементом этой модели является конечно-элементная дискретизация изделия с помощью совокупности конечных элементов (КЭ) заданной формы и объединённых в единую систему, называемую конечно-элементной сеткой.
В данной работе используются КЭ тетраэдральной формы. Они аппроксимируют исходную конструкцию, связываясь между собой в граничных точках - узлах, в каждом из которых вводится по три поступательных степени свободы (для задач механики). Действующие на конструкцию внешние нагрузки приводятся к эквивалентным силам, прикладываемым в узлах конечных элементов. Ограничения на перемещение конструкции (закрепления) также переносятся на КЭ, которыми моделируется исходный объект.
Погрешность конечно-элементной аппроксимации обычно уменьшается с увеличением степени дискретизации моделируемой системы - чем большее количество КЭ участвует в дискретизации (или чем меньше относительные размеры КЭ), тем точнее получаемое решение. Естественно, что более плотное разбиение КЭ приводит к увеличению временных затрат при моделировании.
2. Практическая часть
2.1. Порядок выполнения работы
При проведении статического анализа конструкции детали необходимо выполнить следующие пункты:
- построить трёхмерную модель детали;
- создать "Задачу" для одного или нескольких соприкасающихся твёрдых тел ("клеевое" соединение);
- сгенерировать тетраэдральную конечно-элементную сетку;
- задать материал модели;
- наложить граничные условия, определяющие сущность физического явления, подлежащего анализу;
- выполнить расчёт;
- проанализировать результаты,
- оформить отчет по результатам анализа.
2.2. Подготовка объемной твердотельной модели изделия
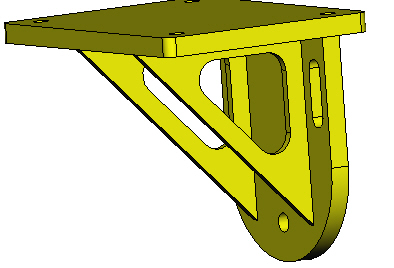
Рассмотрим выполнение статического прочностного расчёта на примере конструкции детали "Кронштейн". Для этого трёхмерная твердотельная модель детали ND:\ Статический анализ. Примеры.\ Кронштейн ( рис. 9.1) загружается в среде T-FLEX CAD.
2.3. Создание "Задачи"
2.3.1. Создание сеточной модели
В строке меню с помощью команды "Анализ|Новая Задача/Конечно-элементный анализ" создается "Задача". В левой стороне окна в панели "Свойства" выбираем тип анализа "Статический ннализ" ( рис. 9.2).
Далее в автоменю нажать опцию "Выбрать все тела" , и при нажатии
, и при нажатии открывается окно создания сетки (
рис.
9.3).
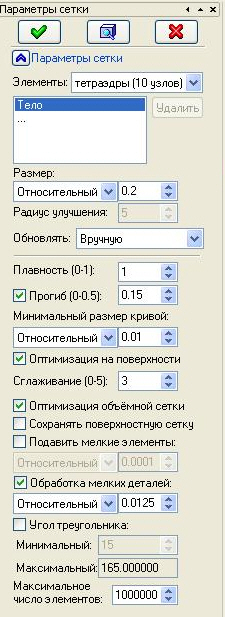
открывается окно создания сетки (
рис.
9.3).
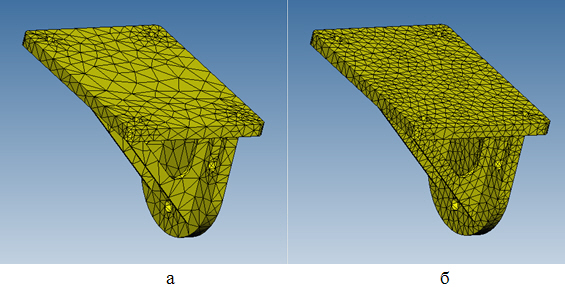
Относительный размер сетки меняем, добиваясь по возможности более однородного распределения формы образующих сетку элементов. Например, на рис. 9.4,а относительный размер сетки 0,2, а на рис. 9.4,б - 0,05.
2.3.2. Назначение материала
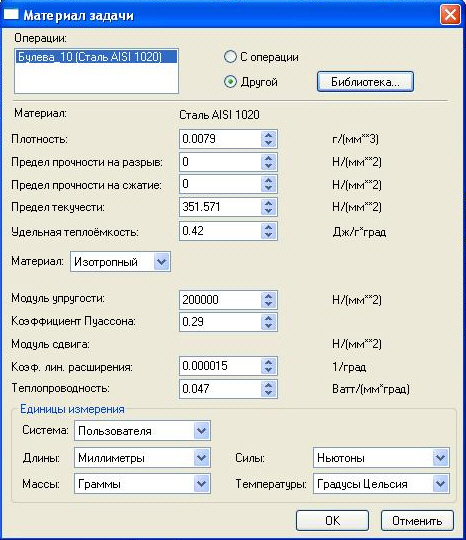
Выбор материала выполняется командой Анализ/Материал. При этом открывается окно "Материал задачи", в котором для изменения материала установить "Другой", нажать "Библиотека", выбрать нужный материал ( рис. 9.5) и нажатием ОК подтвердить выбор. Назначим для модели материал "Сталь/AISI 1020" из библиотеки материалов T- FLEX Анализа.
2.3.3. Наложение граничных условий
В статике роль граничных условий выполняют закрепления и приложенные к системе внешние нагрузки. Для задания закреплений предусмотрены две команды: "Полное закрепление" и "Частичное закрепление".
Команда Анализ\Ограничение\Полное закрепление применяется к вершинам, граням и рёбрам модели. Она определяет, что данный элемент трёхмерного тела полностью неподвижен, т.е. сохраняет своё первоначальное расположение и не меняет своего положения под действием приложенных к системе нагрузок.
Применим эту команду (
рис.
9.6) и укажем с помощью заднюю грань детали. После нажатия
заднюю грань детали. После нажатия появится соответствующий элемент, указывающий на наличие данного граничного условия (
рис.
9.7).
появится соответствующий элемент, указывающий на наличие данного граничного условия (
рис.
9.7).
2.3.4. Задание нагружений
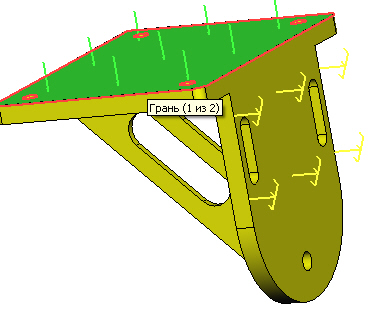
При задании нагружений командой Анализ\ Нагружение\Сила необходимо нажатием указать грань "Корпуса", на которую прикладывается нагрузка (
рис.
9.8). В диалоге свойств команды в поле "Величина" выбирается значение силы (550 Н). Созданная сила равномерно распределится по указанной грани. Изначально направление действия силы берется по нормали к указанной плоской грани. При необходимости направление вектора силы можно задать под любым углом к плоскости.
указать грань "Корпуса", на которую прикладывается нагрузка (
рис.
9.8). В диалоге свойств команды в поле "Величина" выбирается значение силы (550 Н). Созданная сила равномерно распределится по указанной грани. Изначально направление действия силы берется по нормали к указанной плоской грани. При необходимости направление вектора силы можно задать под любым углом к плоскости.
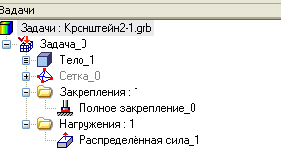
После нажатия получаем в дереве задач (
рис.
9.9) все четыре элемента, необходимых для моделирования: сетка, материал, закрепление, нагружение.
получаем в дереве задач (
рис.
9.9) все четыре элемента, необходимых для моделирования: сетка, материал, закрепление, нагружение.