НОУ ИНТУИТ | Прикладная статистика. Лекция 12: Статистика интервальных данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать программу

Для нахождения рационального объема выборки необходимо сделать следующее.

Этап 1. Выразить зависимость размеров и меры области рассеивания 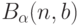$B_\alpha(n,b)$ от числа опытов (см. выше).

Этап 2. Ввести меру неопределенности и записать соотношение между статистической и интервальной неопределенностями.

Этап 3. По результатам этапов 1 и 2 получить выражение для рационального объема выборки.

Для выполнения этапа 1 определим область рассеивания следующим образом. Пусть доверительным множеством 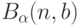$B_{\alpha}(n,b)$ является -мерный куб со сторонами длиною , для которого

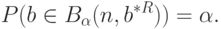
$P(b\in B_{\alpha}(n,b^{*R}))=\alpha.$

Исследуем случайный вектор b^* и

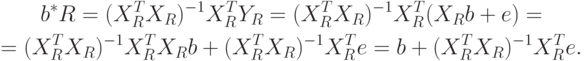
$\begin{gathered} b^*R=(X_R^TX_R)^{-1}X_R^TY_R=(X_R^TX_R)^{-1}X_R^T(X_Rb+e)= \\ =(X_R^TX_R)^{-1}X_R^TX_Rb+(X_R^TX_R)^{-1}X_R^Te=b+(X_R^TX_R)^{-1}X_R^Te. \end{gathered}$

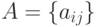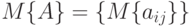Как известно, если элементы матрицы $A = \{a_{ij}\}$ - случайные, т.е. - случайная матрица, то ее математическим ожиданием является матрица, составленная из математических ожиданий ее элементов, т.е. $M\{A\}=\{M\{a_{ij}\}\}$ .

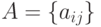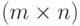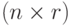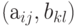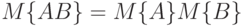Утверждение 1. Пусть $A=\{a_{ij}\}$ и $B=\{b_{ij}\}$ - случайные матрицы порядка $(m \times n)$ и $(n \times r)$ соответственно, причем любая пара их элементов $(а_{ij},b_{kl})$ состоит из независимых случайных величин. Тогда математическое ожидание произведения матриц равно произведению математических ожиданий сомножителей, т.е. $M\{AB\} = M\{A\} M\{B\}$ .

Доказательство. На основании определения математического ожидания матрицы заключаем, что

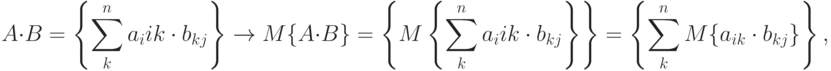
$A\cdot B= \left\{\sum_k^n a_i{ik}\cdot b_{kj}\right\}\rightarrow M\{A\cdot B\}= \left\{M\left\{\sum_k^n a_i{ik}\cdot b_{kj}\right\}\right\}= \left\{\sum_k^n M\{a_{ik}\cdot b_{kj}\}\right\},$

но так как случайные величины $a_{ik}, b_{kj}$ независимы, то

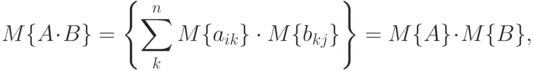
$M\{A\cdot B\}=\left\{\sum_k^n M\{a_{ik}\}\cdot M\{b_{kj}\}\right\}=M\{A\}\cdot M\{B\},$

что и требовалось доказать.

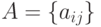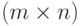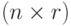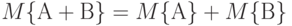Утверждение 2. Пусть $A=\{a_{ij}\}$ и $B=\{b_{ij}\}$ - случайные матрицы порядка $(m\times n)$ и $(n\times r)$ соответственно. Тогда математическое ожидание суммы матриц равно сумме математических ожиданий слагаемых, т.е. $M\{А+В\} = M\{А\} + M\{В\}$ .

Доказательство. На основании определения математического ожидания матрицы заключаем, что

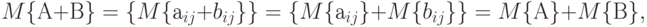
$M\{А+В\} = \{M\{а_{ij}+b_{ij}\}\} = \{M\{а_{ij}\} + M\{b_{ij}\}\} =M\{А\} + M\{В\},$

что и требовалось доказать.

Найдем математическое ожидание и ковариационную матрицу вектора b^* с помощью утверждений 1, 2 и выражения для $b^{*R},$ приведенного выше. Имеем

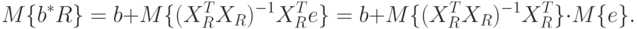
$M\{b^*R\}=b+M\{(X_R^TX_R)^{-1}X_R^Te\}=b+M\{(X_R^TX_R)^{-1}X_R^T\}\cdot M\{e\}.$

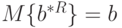Но так как $M\{e\}=0$ , то $M\{b^{*R}\}=b$ . Это означает, что оценка МНК является несмещенной.

Найдем ковариационную матрицу:

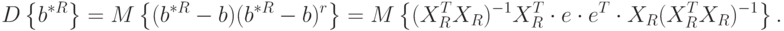
$D\left\{b^{*R}\right\}=M\left\{(b^{*R}-b)(b^{*R}-b)^r\right\}= M\left\{(X_R^TX_R)^{-1}X_R^T\cdot e\cdot e^T\cdot X_R(X_R^TX_R)^{-1}\right\}.$

Можно доказать, что

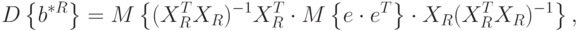
$D\left\{b^{*R}\right\}=M\left\{(X_R^TX_R)^{-1}X_R^T\cdot M\left\{e\cdot e^T\right\}\cdot X_R(X_R^TX_R)^{-1}\right\},$

но

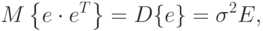
$M\left\{e\cdot e^T\right\}=D\{e\}=\sigma^2 E,$

поэтому

$D\left\{b^{*R}\right\}=M\left\{(X_T^RX_R)^{-1}X_R^T(\sigma^2 E)X_R(X_R^TX_R)^{-1}\right\}=\sigma^2 M\{(X_R^TX_R)^{-1}\}.$

Как выяснено ранее, для достаточно большого количества опытов выполняется приближенное равенство

$(X_R^TX_R)^{-1}\approx\frac{1}{n}E,$

( 51)

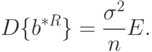
$D\{b^{*R}\}=\frac{\sigma^2}{n}E.$

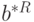Осталось определить вид распределения вектора $b^{*R}$ . Из выражения для 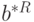$b^{*R}$ , приведенного выше, и асимптотического соотношения (51) следует, что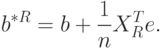

$b^{*R}=b+\frac{1}{n}X_R^Te.$

Можно утверждать, что вектор 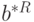$b^{*R}$ имеет асимптотически нормальное распределение, т.е.

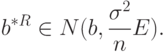
$b^{*R}\in N(b,\frac{\sigma^2}{n}E).$

Тогда совместная функция плотности распределения вероятностей случайных величин 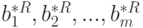$b^{*R}_1, b^{*R}_2,..., b^{*R}_m$ будет иметь вид:

$f(b^{*R})=\frac{1}{(2\pi)^{m/2}\cdot(\det C)^{1/2}}\cdot\exp[-\frac12(b^{*R}-b)^T\cdot C^{-1}\cdot(b^{*R}-b)],$

( 52)

где

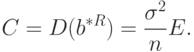
$C=D(b^{*R})=\frac{\sigma^2}{n}E.$

Тогда справедливы соотношения

$C^{-1}=\frac{n}{\sigma^2}E,\;\det C=\det\left(\frac{n}{\sigma^2}E\right)=\left(\frac{\sigma^2}{n}\right)^m.$

Подставим в формулу (52), получим

$\begin{aligned} &f(b^{*R})=\frac{1}{(2\pi)^{m/2}\cdot(\sigma^2/n)^{m/2}}\cdot\exp[-\frac{n}{2\sigma^2}(b^{*R}-b)^T\cdot C^{-1}\cdot(b^{*R}-b)]= \\ &=\frac{1}{(\sigma\sqrt{2\pi/n})^m}\exp[-\frac{n}{2\sigma^2}(b^{*R}-b)^T\cdot C^{-1}\cdot(b^{*R}-b)]= \\ &=\frac{1}{(\sigma\sqrt{2\pi/n})^m}\exp[-\frac{n}{2\sigma^2}(\beta_1^2+\beta_2^2+...+\beta_m^2)], \end{aligned}$

где

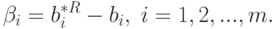
$\beta_i=b_i^{*R}-b_i,\;i=1,2,...,m.$

Вычислим асимптотическую вероятность попадания описывающего реальность вектора параметров в -мерный куб с длиной стороны, равной 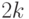, и с центром $b^{*R}$ .

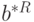$\begin{gathered} P(-k<\beta_1<k,-k<\beta_2<k,...,-k<\beta_m<k)= \\ =\frac{1}{(\sigma\sqrt{2\pi/n})^m}\{\int\limits_{-k}^k..\int\limits_{-k}^k\exp[-\frac{n}{2\sigma^2}(\beta_1^2+\beta_2^2+...+\beta_m^2)]\cdot d\beta_1...d\beta_m\}= \\ =\frac{1}{(\sigma\sqrt{2\pi/n})^m}\{\int\limits_{-k}^k\exp[-\frac{n}{2\sigma^2}\beta_1^2]d\beta_1...\int\limits_{-k}^k\exp[-\frac{n}{2\sigma^2}\beta_i^2]d\beta_i\}. \end{gathered}$

Сделаем замену

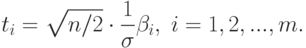
$t_i=\sqrt{n/2}\cdot\frac{1}{\sigma}\beta_i,\;i=1,2,...,m.$

Тогда

$\begin{aligned} &P=P(-k<\beta_1<k,-k<\bela_2<k,...,-k<\beta_m<k)= \\ &=\frac{(\sigma\sqrt{2/n})^m}{\sigma\sqrt{2\pi/n})^m}[\int\limits_{-T}^T e^{-t^2}dt]^m = [(1/\sqrt{\pi})\int\limits_{-T}^T e^{-t^2}dt]^m]=[\Phi_0(T)]^m, \end{aligned}$

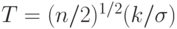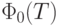где $T = (n/2)^{1/2}(k/\sigma)$ , а $\Phi_0(T)$ - интеграл Лапласа,

$\Phi_0(T)=\Phi(\sqrt{2}T)-\Phi(-\sqrt{2}T),$

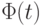где $\Phi(t)$ - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Из последнего соотношения получаем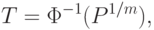

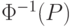$T=\Phi^{-1}(P^{1/m}),$

где $\Phi^{-1}(P)$ - обратная функция Лапласа. Отсюда следует, что

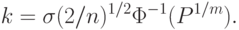$k=\sigma(2/n)^{1/2}\Phi^{-1}(P^{1/m}).$

( 53)

Напомним, что доверительная область 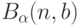$B_{\alpha}(n,b)$ - это -мерный куб, длина стороны которого равна , т.е.

$P(b\in B_{\alpha}(n,b))=P(-K<\beta_1<K,-K<\beta_2<K,...,-K<\beta_m<K)=\alpha.$

Подставляя $P=\alpha$ в формулу (53), получим

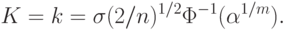$K=k=\sigma(2/n)^{1/2}\Phi^{-1}(\alpha^{1/m}).$

( 54)

Соотношение (54) выражает зависимость размеров доверительной области (т.е. длины ребра куба ) от числа опытов , среднего квадратического отклонения $\sigma$ ошибки и доверительной вероятности $\alpha$ . Это соотношение понадобится для определения рационального объема выборки.

Переходим к этапу 2. Необходимо ввести меру разброса (неопределенности) и установить соотношение между статистической и интервальной (метрологической) неопределенностями в соответствии с ранее сформулированным общим подходом.

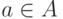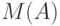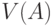Пусть - некоторое измеримое множество точек в -мерном евклидовом пространстве, характеризующее неопределенность задания вектора $a\in A$ . Тогда необходимо ввести некую меру M(A) , измеряющую степень неопределенности. Такой мерой может служить -мерный объем V(A) множества (т.е. его мера Лебега или Жордана), M(A)=V(A) .

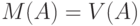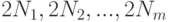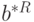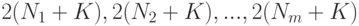Пусть - -мерный параллелепипед, характеризующий интервальную неопределенность. Длины его сторон равны значениям нотн 2N_1, 2N_2,..., 2N_m , а центр (точка пересечений диагоналей параллелепипеда) находится в точке $b^{*R}$ . Пусть - измеримое множество точек, характеризующее общую неопределенность. В рассматриваемом случае это -мерный параллелепипед, длины сторон которого равны 2(N_1+K),2(N_2+K),...,2(N_m+K) , а центр находится в точке 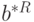$b^{*R}$ . Тогда

( 55)

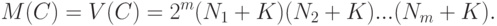( 56)

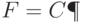Справедливо соотношение (49), согласно которому M(C)=M(P)+M(F) , где множество $F=C\P$ характеризует статистическую неопределенность.

На этапе 3 получаем по результатам этапов 1 и 2 выражение для рационального объема выборки. Найдем то число опытов, при котором статистическая неопределенность составит $\delta$ 100% от общей неопределенности, т.е. согласно правилу (50)

$M(F)=M(C)-M(P)=\delta M(C),$

( 57)

где $0<\delta<1$ . Подставив (55) и (56) в (57), получим

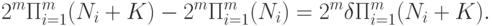
$2^m\Pi_{i=1}^m(N_i+K)-2^m\Pi_{i=1}^m(N_i)=2^m\delta\Pi_{i=1}^m(N_i+K).$

Следовательно, 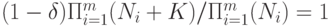$(1-\delta)\Pi_{i=1}^m(N_i+K)/\Pi_{i=1}^m(N_i)=1$ .

Преобразуем эту формулу:

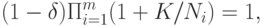
$(1-\delta)\Pi_{i=1}^m(1+K/N_i)=1,$

откуда

$\Pi_i^m(1+K/N_i)=1/(1-\delta).$

Если статистическая погрешность мала относительно метрологической, т.е. величины 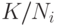K/N_i малы, то

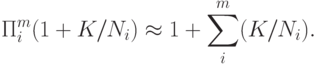
$\Pi_i^m(1+K/N_i)\approx 1+\sum_i^m(K/N_i).$

При 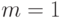m = 1 эта формула является точной. Из нее следует, что для дальнейших расчетов можно использовать соотношение

$1+\sum_i^m(K/N_i)=1/(1-\delta).$

Отсюда нетрудно найти :

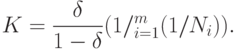$K=\frac{\delta}{1-\delta}(1/\sun_{i=1}^m(1/N_i)).$

( 58)

Подставив в формулу (58) зависимость 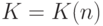K=K(n) , полученную в формуле (54), находим приближенное (асимптотическое) выражение для рационального объема выборки:

$n_{\textit{рац}}=2\left(\frac{1-\delta}{\delta}\sigma\sum_{i=1}^m(1/N_i)\cdot\Phi^{-1}(\alpha^{1/m})\right)^2.$

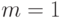При m = 1 эта формула также справедлива, более того, является точной.

Переход от произведения к сумме является обоснованным при достаточно малом $\delta$ , т.е. при достаточно малой статистической неопределенности по сравнению с метрологической. В общем случае можно находить и затем рациональный объем выборки тем или иным численным методом.

Пример 1. Представляет интерес определение nрац для случая, когда m = 2 , поскольку простейшая линейная регрессия с m =2 широко применяется. В этом случае базовое соотношение имеет вид

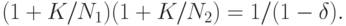
$(1 + K/N_1)(1 + K/N_2) = 1/(1 - \delta).$

Решая это уравнение относительно , получаем

$K=0.5\{-(N_1 + N_2) + [(N_1 + N_2)^2 + 4 N_1N_2 (\delta/(1 - \delta)]^{1/2}\}.$

Далее, подставив в формулу (54), получим уравнение для рационального объема выборки в случае m = 2 :

$\sigma(2/n)^{1/2}\Phi^{-1}(\alpha^{1/2})=0.5\{-(N_1+N_2)+[(N_1+N_2)^2+4N_1N_2(\delta/(1-\delta)]^{1/2}\}.$

Следовательно,

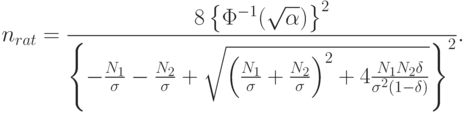
$n_{rat}=\frac{8\left\{\Phi^{-1}(\sqrt{\alpha})\right\}^2}{\left\{-\frac{N_1}{\sigma}-\frac{N_2}{\sigma}+\sqrt{\left(\frac{N_1}{\sigma}+\frac{N_2}{\sigma}\right)^2+4\frac{N_1N_2\delta}{\sigma^2(1-\delta)}}\right\}^2}.$

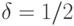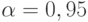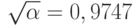При использовании "принципа уравнивания погрешностей" согласно [ [ 1.15 ] ] $\delta=1/2$ . При доверительной вероятности $\alpha=0,95$ имеем $\sqrt{\alpha}=0,9747$ и согласно [ [ 2.1 ] ] $\Phi^{-1}(\sqrt{\alpha})=1,954$ . Для этих численных значений

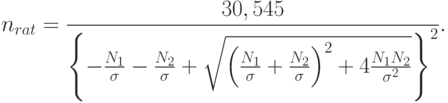
$n_{rat}=\frac{30,545}{\left\{-\frac{N_1}{\sigma}-\frac{N_2}{\sigma}+\sqrt{\left(\frac{N_1}{\sigma}+\frac{N_2}{\sigma}\right)^2+4\frac{N_1N_2}{\sigma^2}\right\}^2}.$

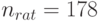Если $\frac{N_1}{\sigma}=\frac{N_2}{\sigma}=0,1$ то $n_{rat}=4455$ . Если же $\frac{N_1}{\sigma}=\frac{N_2}{\sigma}=0,5$ то $n_{rat}=178$ . Если первое из этих чисел превышает обычно используемые объемы выборок, то второе находится в "рабочей зоне" регрессионного анализа.

Парная регрессия. Наиболее простой и одновременно наиболее широко применяемый частный случай парной регрессии рассмотрим подробнее. Модель имеет вид

$y_i=ax_i+b+\epsilon_i,\;i=1,2,...,n.$

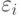Здесь x_i - значения фактора (независимой переменной), y_i - значения отклика (зависимой переменной), $\varepsilon_i$ - статистические погрешности, a, b - неизвестные параметры, оцениваемые методом наименьших квадратов. Она переходит в модель (используем альтернативную запись линейной модели)

$y=X\beta+\varepsilon,$

если положить

$y= \begin{pmatrix} y_1 \\ \ldots \\ y_n \end{pmatrix},\quad X= \begin{pmatrix} x_1 & 1 \\ \ldots & \ldots \\ x_n & 1 \end{pmatrix},\quad \varepsilon= \begin{pmatrix} \varepsilon_1 \\ \ldots \\ \varepsilon_n \end{pmatrix},\quad \beta= \begin{pmatrix} a \\ b \end{pmatrix}.$

Естественно принять, что погрешности факторов описываются матрицей

$\Delta_x=\alpha= \begin{pmatrix} \Delta x_1 & 0 \\ \ldots & \ldots \\ \Delta x_n & 0 \end{pmatrix}= \begin{pmatrix} \alpha_1 & 0 \\ \ldots & \ldots \\ \alpha_n & 0 \end{pmatrix}.$

В рассматриваемой модели интервального метода наименьших квадратов

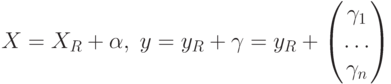
$X=X_R+\alpha,\;y=y_R+\gamma=y_R+ \begin{pmatrix} \gamma_1 \\ \ldots \\ \gamma_n \end{pmatrix}$

где

- наблюдаемые (т.е. известные статистику) значения фактора и отклика, X_R, y_R

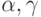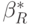- истинные значения переменных, $\alpha,\gamma$ - погрешности измерений переменных. Пусть $\beta^*$ - оценка метода наименьших квадратов, вычисленная по наблюдаемым значениям переменных, $\beta_R^*$ - аналогичная оценка, найденная по истинным значениям. В соответствии с ранее проведенными рассуждениями

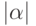$\beta^*-\beta=[-(X_0^TX_0)^{-1}\Delta(X_0^TX_0)^{-1}X_0^T+(X_0^TX_0)^{-1}\alpha^T]y_0+(X_0^TX_0)^{-1}X_0^T\gamma$

( 59)

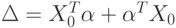с точностью до бесконечно малых более высокого порядка по $|\alpha|$ и $|\gamma|$ . В формуле (59) использовано обозначение $\Delta=X_0^T\alpha+\alpha^TX_0$ . Вычислим правую часть в (59), выделим главный линейный член и найдем нотну.

Легко видеть, что

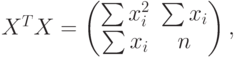$X^TX= \begin{pmatrix} \sum x_i^2 & \sum x_i \\ \sum x_i & n \end{pmatrix},$

( 60)

где суммирование проводится от 1 до . Для упрощения обозначений в дальнейшем до конца настоящего параграфа не будем указывать эти пределы суммирования. Из (60) вытекает, что

$(X^TX)^{-1}= \left. \begin{pmatrix} n & -\sum x_i \\ -\sum x_i & \sum x_i^2 \end{pmatrix} \right/ \left[ n\sum x_i^2-\left(\sum x_i\right)^2 \right].$

( 61)

Легко подсчитать, что

$X^T\alpha+\alpha^TX= \begin{pmatrix} 2\sum x_i\alpha_i & \sum\alpha_i \\ \sum\alpha_i & n \end{pmatrix}.$

( 62)

Положим

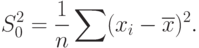
$S_0^2=\frac{1}{n}\sum(x_i-\overline{x})^2.$

Тогда знаменатель в (61) равен 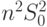n^2S_0^2 . Из (61) и (62) следует, что

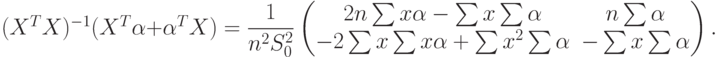$(X^TX)^{-1}(X^T\alpha+\alpha^TX)=\dfrac{1}{n^2S_0^2} \begin{pmatrix} 2n\sum x\alpha-\sum x\sum\alpha & n\sum\alpha \\ -2\sum x\sum x\alpha+\sum x^2\sum\alpha & -\sum x\sum\alpha \end{pmatrix}.$

( 63)

Здесь и далее опустим индекс , по которому проводится суммирование. Это не может привести к недоразумению, поскольку всюду суммирование проводится по индексу в интервале от 1 до . Из (61) и (63) следует, что

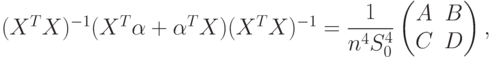$(X^TX)^{-1}(X^T\alpha+\alpha^T X)(X^TX)^{-1}=\dfrac{1}{n^4S_0^4}\begin{pmatrix}A & B \\ C & D \end{pmatrix},$

( 64)

где

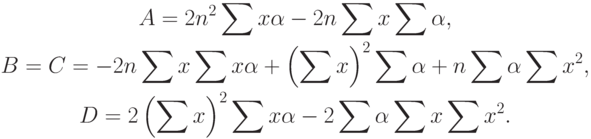
$\begin{gathered} A=2n^2\sum x\alpha-2n\sum x\sum\alpha, \\ B=C=-2n\sum x\sum x\alpha + \left(\sum x\right)^2\sum\alpha+n\sum\alpha\sum x^2, \\ D=2\left(\sum x\right)^2\sum x\alpha-2\sum\alpha\sum x\sum x^2. \end{gathered}$

Наконец, вычисляем основной множитель в (59)

$(X^TX)^{-1}(X^T\alpha+\alpha^TX)(X^TX)^{-1}X^T=\dfrac{1}{n^4S_0^4} \begin{pmatrix} z_{11}&z_{12}&\ldots&z_{1i}&\ldots&z_{1n} \\ z_{21}&z_{22}&\ldots&z_{2i}&\ldots&z_{2n} \end{pmatrix},$

( 65)

где

$z_{1i}=Ax_i+B, z_{2i}=Cx_i+D,\;i=1,2,...,n.$

Перейдем к вычислению второго члена с $\alpha$ в (59). Имеем

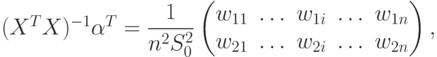$(X^TX)^{-1}\alpha^T=\dfrac{1}{n^2S_0^2} \begin{pmatrix} w_{11} & \ldots & w_{1i} & \ldots & w_{1n} \\ w_{21} & \ldots & w_{2i} & \ldots & w_{2n} \end{pmatrix},$

( 67)

где

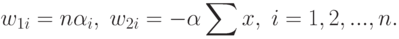
$w_{1i}=n\alpha_i,\;w_{2i}=-\alpha\sum x,\;i=1,2,...,n.$

Складывая правые части (65) и (67) и умножая на , получим окончательный вид члена с $\alpha$ в (59):

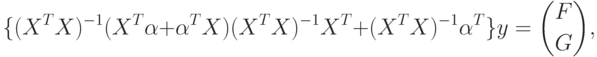$\{(X^TX)^{-1}(X^T\alpha+\alpha^TX)(X^TX)^{-1}X^T+(X^TX)^{-1}\alpha^T\}y={F\choose G},$

( 68)

где

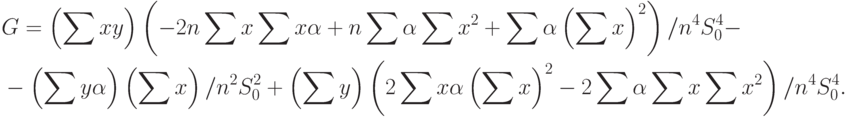
$\begin{aligned} &G=\left(\sum xy\right)\left(-2n\sum x\sum x\alpha+n\sum\alpha\sum x^2+\sum\alpha\left(\sum x\right)^2\right)/n^4S_0^4- \\ &-\left(\sum y\alpha\right)\left(\sum x\right)/n^2S_0^2+\left(\sum y\right)\left(2\sum x\alpha\left(\sum x\right)^2-2\sum\alpha\sum x\sum x^2\right)/n^4S_0^4. \end{aligned}$

Для вычисления нотны выделим главный линейный член. Сначала найдем частные производные. Имеем

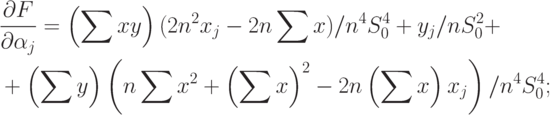$\begin{aligned} &\frac{\partial F}{\partial\alpha_j}=\left(\sum xy\right)(2n^2x_j-2n\sum x)/n^4S_0^4+y_j/nS_0^2+ \\ &+\left(\sum y\right)\left(n\sum x^2+\left(\sum x\right)^2-2n\left(\sum x\right)x_j\right)/n^4S_0^4; \end{aligned}$

( 70)

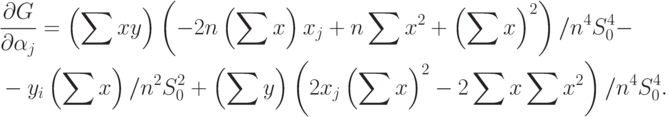
$\begin{aligned} &\frac{\partial G}{\partial\alpha_j}=\left(\sum xy\right)\left(-2n\left(\sum x\right)x_j+n\sum x^2+\left(\sum x\right)^2\right)/n^4S_0^4- \\ &-y_i\left(\sum x\right)/n^2S_0^2+\left(\sum y\right)\left(2x_j\left(\sum x\right)^2-2\sum x\sum x^2\right)/n^4S_0^4. \end{aligned}$

Если ограничения имеют вид

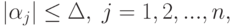
$|\alpha_j|\le\Delta,\;j=1,2,...,n,$

то максимально возможное отклонение оценки a^*

параметра

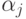из-за погрешностей $\alpha_j$ таково:

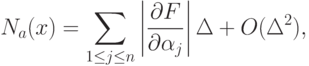
$N_a(x)=\sum_{1\le j\le n}\left|\frac{\partial F}{\partial\alpha_j}\right|\Delta+O(\Delta^2),$

где производные заданы формулой (70).

Пример 2. Пусть вектор (x,y) имеет двумерное нормальное распределение с нулевыми математическими ожиданиями, единичными дисперсиями и коэффициентом корреляции $\rho$ . Тогда

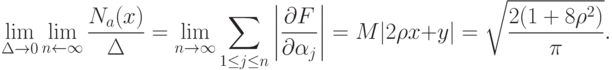$\lim_{\Delta\rightarrow 0}\lim_{n\leftarrow\infty}\frac{N_a(x)}{\Delta}=\lim_{n\rightarrow\infty}\sum_{1\le j\le n}\left|\frac{\partial F}{\partial\alpha_j}\right|=M|2\rho x+y|=\sqrt{\frac{2(1+8\rho^2)}{\pi}}.$

( 71)

При этом

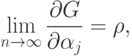
$\lim_{n\rightarrow\infty}\frac{\partial G}{\partial\alpha_j}=\rho,$

следовательно, максимально возможному изменению параметра b^*

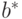соответствует сдвиг всех x_i

в одну сторону, т.е. наличие систематической ошибки при определении

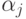-ов. В то же время согласно (71) значения $\alpha_j$ в асимптотике выбираются по правилу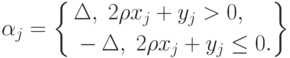

$\alpha_j= \left\{ \begin{aligned} &\Delta,\;2\rho x_j+y_j>0, \\ &-\Delta,\;2\rho x_j+y_j\le 0. \end{aligned} \right\}$

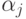Таким образом, максимальному изменению a^* соответствуют не те $\alpha_j$ , что максимальному изменению 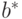b^* . В этом - новое по сравнению с одномерным случаем. В зависимости от вида ограничений на возможные отклонения, в частности, от вида метрики в пространстве параметров, будут "согласовываться" отклонения по отдельным параметрам. Ситуация аналогична той, что возникает в классической математической статистике в связи с оптимальным оцениванием параметров. Если параметр одномерен, то ситуация с оцениванием достаточно прозрачна - есть понятие эффективных оценок, показателем качества оценки является средний квадрат ошибки, а при ее несмещенности - дисперсия. В случае нескольких параметров возникает необходимость соизмерить точность оценивания по разным параметрам. Есть много критериев оптимальности (см., например, [ [ 12.21 ] ]), но нет признанных правил выбора среди них.

Вернемся к формуле (59). Интересно, что отклонения вектора параметров, вызванные отклонениями значений факторов $\alpha$ и отклика $\gamma$ , входят в (59) аддитивно. Хотя

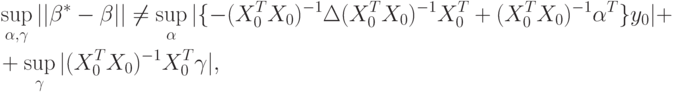
$\begin{aligned} &\sup_{\alpha,\gamma}||\beta^*-\beta||\ne\sup_{\alpha}|\{-(X_0^TX_0)^{-1} \Delta(X_0^TX_0)^{-1}X_0^T+(X_0^TX_0)^{-1}\alpha^T\}y_0|+ \\ &+\sup_\gamma|(X_0^TX_0)^{-1}X_0^T\gamma|, \end{aligned}$

но для отдельных компонент (не векторов!) имеет место равенство.

В случае парной регрессии

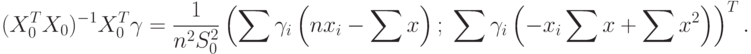$(X_0^TX_0)^{-1}X_0^T\gamma=\frac{1}{n^2S_0^2} \left(\sum\gamma_i\left(nx_i-\sum x\right);\;\sum\gamma_i\left(-x_i\sum x+\sum x^2\right)\right)^T.$

( 72)

Из формул (68), (69) и (72) следует, что

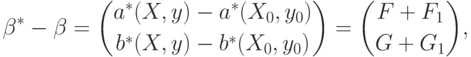
$\beta^*-\beta={{a^*(X,y)-a^*(X_0,y_0)}\choose{b^*(X,y)-b^*(X_0,y_0)}}={{F+F_1}\choose{G+G_1}},$

где

и

определены в (69), а

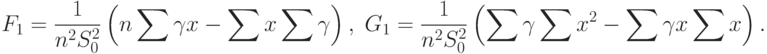
$F_1=\frac{1}{n^2S_0^2}\left(n\sum\gamma x-\sum x\sum\gamma\right),\; G_1=\frac{1}{n^2S_0^2}\left(\sum\gamma\sum x^2-\sum\gamma x\sum x\right).$

Итак, продемонстрирована возможность применения основных подходов статистики интервальных данных в регрессионном анализе. Пример практического применения этих подходов при оценивании зависимости затрат от объема выпуска продукции дан в статье: Гуськова Е.А., Орлов А.И. Интервальная линейная парная регрессия (обобщающая статья). - Журнал "Заводская лаборатория". 2005. Т.71. No.3. С.57-63.

Дальше >>

Прикладная статистика

Прикладная статистика

Статистика интервальных данных

Вопросы и ответы

Студенты

Авторизоваться

Прикладная статистика

Прикладная статистика

Статистика интервальных данных

Вопросы и ответы

Студенты